| | Olympiodiose |  |
|
+31Dijkschneier SherlocK mizmaz reda-t smash stranger Emerson Perelman dima_amazigh Ayoub M-H EINSTEINIUM Sylphaen neohs noirouge majdouline soukki abdellah=einstein issam erriahi Thalès yassine-516 houssam110 marouan777 einstein20 darkpseudo albertmath otman1994 ayyoub Psi just-abdess radouane_BNE samix 35 participants |
|
| Auteur | Message |
|---|
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 18:22 Ven 18 Déc 2009, 18:22 | |
| bonsoir oué c sa .. je savé po la Lemme de titu
ma démosntrastion se basé sur chebychev , les moyennes et la fonction ke jé déja cité !!
a toi !! | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 18:26 Ven 18 Déc 2009, 18:26 | |
| Solution ( sauf erreur biensure) on a (z+1)}\geq&space;\sum&space;\frac{x^{4}}{x(y+1)(z+1)}\geq&space;\frac{(x^{2}+y^{2}+z^{2})^{2}}{\sum&space;x+xy+xz+xyz}=&space;\frac{(x^{2}+y^{2}+z^{2})^{2}}{x+y+z+2(xy+yz+zx)+3xyz}=A) c'est facile de montrer que 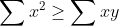 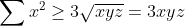 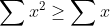 donc ^{2}}{4(\sum&space;x^{2})}\geq&space;\frac{(\sum&space;x^{2})}{4}\geq&space;\frac{3}{4})
Dernière édition par just-abdess le Sam 19 Déc 2009, 13:33, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 19:02 Ven 18 Déc 2009, 19:02 | |
| aussi je propose une solution....sauf erreur... l'inégalité est équivalente à: \geq%203(x+y+z+xy+yz+zx+2)) par symétrie des rôles supposons que x>=y>=z par Chebyshev on a donc:  CQFD | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 19:50 Ven 18 Déc 2009, 19:50 | |
| bonsoir just abdess:
pour l'erreur que tu as commise dans ta démonstration...est du genre logique...en effet:
on veut démontrer cette proposition: (∀x£]0,+∞[):f(x)=x
donc la négation c'est:(∃x£]0,+∞[):f(x)≠x
il existe un x....
donc t'as fait il existe un x de ]0,+∞[:f(x)≠x<=>(∃x£]0,+∞[):f(x)>x ou (∃x£]0,+∞[):f(x)<x
donc on a f(x)<x ...mais ça ne nous permet pas d'écrire que f(y)<y...car on a il existe un x de IR+ et nn pas pour tout x de IR+....ainsi ton raisonnement est incorrect..... | |
|
  | |
einstein20
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : oujda
Date d'inscription : 14/04/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 20:05 Ven 18 Déc 2009, 20:05 | |
| bah slt tou l'monde voisi un exo d'olymp:
calculer A ;A=1/1.2 + 1/3.4 +...1/(2n-1)2n - 1/n+1 -1/n+2 -...-1/2n | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 22:31 Ven 18 Déc 2009, 22:31 | |
| pourtant je propose la solution suivante pour le problème de abdellah: donc pour a=b=x=y=1 on aura f(1)=1 pour a=b=x=y on aura: [f(x)]²=f(x²) alors notre relation devient: +f(y^2)}{f(a^2)+f(b^2)%20}=\frac{x^2+y^2}{a^2+b^2}<br />) donc pour x²=X et y²=Y et a²=A et b²=B on aura : +f(y)}{f(a)+f(b)%20}=\frac{x+y}{a+b}) avec V(xy)=V(ab)<=>xy=ab pour y=1 on aura ab=x alors l'équation devient: +1}{f(a)+f(b)%20}=\frac{ab+1}{a+b}) <=>a+b+a.f(ab)+b.f(ab)=f(a)+f(b)+ab.f(a)+ab.f(b) pour a=b on aura: 2a+2a.f(a²)=2f(a)+2a²f(a) or f(a²)=[f(a)]² alors: a+a.[f(a)]²=f(a)+a²f(a) <=>(a-f(a))(1-a.f(a))=0 d'où f(a)=a ou f(a)=1/a alors (∀x£IR+*) f(x)=x
(∀x£IR+*) f(x)=1/x | |
|
  | |
SherlocK
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : Khouribga, Maroc
Date d'inscription : 22/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Ven 18 Déc 2009, 22:34 Ven 18 Déc 2009, 22:34 | |
| - einstein20 a écrit:
- bah slt tou l'monde voisi un exo d'olymp:
calculer A ;A=1/1.2 + 1/3.4 +...1/(2n-1)2n - 1/n+1 -1/n+2 -...-1/2n C'est déjà posté  | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Sam 19 Déc 2009, 13:33 Sam 19 Déc 2009, 13:33 | |
| Re oui ta raison majdouline ma solution est fausse , merci ^^ | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Sam 19 Déc 2009, 17:17 Sam 19 Déc 2009, 17:17 | |
| bonsoir  ..... on attend encore ton exo Dijkschneier!!!!!!!!!!!!!!! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Sam 19 Déc 2009, 18:15 Sam 19 Déc 2009, 18:15 | |
| - majdouline a écrit:
- bonsoir
 ..... .....
on attend encore ton exo Dijkschneier!!!!!!!!!!!!!!! J'ai pas vraiment d'exercice sur la conscience à proposer.. Je vous laisse la main. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 21 Déc 2009, 20:34 Lun 21 Déc 2009, 20:34 | |
| Comme tous le monde est absent je pose cette exo ^^ Soit a,b,c>0 M.Q  | |
|
  | |
issam erriahi
Expert sup

 Nombre de messages : 1102 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 11:21 Jeu 24 Déc 2009, 11:21 | |
| | |
|
  | |
issam erriahi
Expert sup

 Nombre de messages : 1102 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 | |
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 14:11 Jeu 24 Déc 2009, 14:11 | |
| je poste la solution de l'inégalité :  par Am-Gm on a: }{4(ab+bc+ca)}+\frac{2(ab+bc+ca)}{3(a+b)(b+c)}) la somme cyclique donne :  il est bien connu que (a+b)(b+c)(c+a)≥8abc ...alors : (a+c)(b+c)}\leq%20\frac{17}{6}+\frac{1}{6}=3) CQFD...
Dernière édition par majdouline le Jeu 24 Déc 2009, 20:02, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 14:40 Jeu 24 Déc 2009, 14:40 | |
| | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Jeu 24 Déc 2009, 18:30 Jeu 24 Déc 2009, 18:30 | |
| Petite faute de tape Majdouline ^^ C'est 17/6 + 1/6 pas 3/2+1/6 . Pour l'exo on a :  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Dim 27 Déc 2009, 13:24 Dim 27 Déc 2009, 13:24 | |
| Salut tous le monde ^^
Je poste cet exo pour faire bouger le topic un petit peut =P
C'est un peu facile mais bon ^^
Déterminez toutes les fonctions de l'ensemble des nombres réels dans
lui-même
telles que
f(x - f(y)) = f(f(y)) + xf(y) + f(x) - 1.
| |
|
  | |
stranger
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 31
Date d'inscription : 13/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 28 Déc 2009, 10:14 Lun 28 Déc 2009, 10:14 | |
| s=\frac{1*3}{3*5}+\frac{2*4}{5*7}+.......+\frac{(n-1)*(n+1)}{(2n-1)*(2n+1)}+......+\frac{1004*1006}{2009*2011} | |
|
  | |
einstein20
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : oujda
Date d'inscription : 14/04/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 28 Déc 2009, 22:23 Lun 28 Déc 2009, 22:23 | |
| slt tou le monde moi aussi j'ai passé le 2em test d'olymp mai le 4em exo je pense ke la solution de SYLPHAEN n'est pa just kar (apd) est strictement inferieur a 108
je peu vou dezmentre ca si vous voulez | |
|
  | |
einstein20
Maître

 Nombre de messages : 102 Nombre de messages : 102
Age : 31
Localisation : oujda
Date d'inscription : 14/04/2008
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 28 Déc 2009, 22:23 Lun 28 Déc 2009, 22:23 | |
| | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Lun 28 Déc 2009, 22:50 Lun 28 Déc 2009, 22:50 | |
| C'est la solution officielle -_-'' | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 30 Déc 2009, 18:55 Mer 30 Déc 2009, 18:55 | |
| - Sylphaen a écrit:
Déterminez toutes les fonctions de l'ensemble des nombres réels dans
lui-même
telles que
f(x - f(y)) = f(f(y)) + xf(y) + f(x) - 1.
Il serait temps de proposer ta solution.. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 30 Déc 2009, 19:27 Mer 30 Déc 2009, 19:27 | |
| On pose : f(y)=x L'équation devient : f(0)=2f(x)+x²-1 On pose x=0 f(0)=2f(0)-1 d'où f(0)=1 Puis on trouve : f(x)=1-x²/2 Sauf erreur ..  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 30 Déc 2009, 19:51 Mer 30 Déc 2009, 19:51 | |
| Le fait de poser %20=%20x) puis 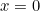 suppose que 0 possède au moins un antécédent par 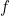 . Ce qui nécessite d'être prouver.. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  Mer 30 Déc 2009, 20:22 Mer 30 Déc 2009, 20:22 | |
| Oui désolé j'avais pas remarquer >.<
Je vais rectifier .. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Olympiodiose Sujet: Re: Olympiodiose  | |
| |
|
  | |
| | Olympiodiose |  |
|
