| | Discusion du premier JOPSM; |  |
|
+14samix just-abdess master reda-t Dijkschneier kirua regulator abdellah=einstein Sylphaen Ayoub M-H darkpseudo majdouline houssam110 MohE 18 participants |
|
| Auteur | Message |
|---|
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Discusion du premier JOPSM; Sujet: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 13:22 Jeu 28 Jan 2010, 13:22 | |
| Ce topic est ouvert pour la discusion des Problèmes du premier JOPSM, la discusion est ouverte pour tout les forumistes. vous pouvez proposer vos solutions pour les dans ce topic; je posterai la mienne après dans ce topic; Bonne chance pour les prochains tours.le sujet est téléchargable depuis ce lien: http://img48.xooimage.com/files/7/3/f/jopsm-12-180c3af.pdf | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 13:55 Jeu 28 Jan 2010, 13:55 | |
| bonjour.
Félécitations aux gagnants..
javé des occupations hier ...
je donne cke jé trouvé ..
1er exo ..
il suffit de tracer le point O le centre ABCD apres on fé un cercle don R=1 et le centre =O
silya un point dans le cercle kya la meme couleur de O ...
si tous les points du cercles sont de la meme couleur
il suffit de de tracer un triangle (motasawi sa9ayn )dans H telle que OH =1 et H £ (C)
de 1ere vue je vois ke pôur le 3eme exo il sagissé de voir ke linego est homogene vu ke f(a;b;c)=f(ka;kb;kc) apres on suppose a+b+c=1 c po sur mais c ke jé vu de 12-14h
jesper ke seré présent dans les prochains JOPSM
VIVA ALGERIE ^^
A+
A+ | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 14:01 Jeu 28 Jan 2010, 14:01 | |
| aussi.. je viens juste de voir ce topic.....et je trouve que c'est une très bonne idée cette compétition là^^ ...je propose la solution du deuxième: on a: \Leftrightarrow%20n=\frac{(m+1)(m-1)}{3}\Rightarrow%203\mid%20m+1\textit{%20ou%20}%203\mid%20m+1) alors m+1=3k(k£Z) ou m-1=3k'(k'£Z) <=>m=3k-1 ou m=3k'+1 si m=3k-1 alors : 3n+1=(3k-1)²<=>3n=9k²-6k <=>n=3k²-2k<=> n+1=k²+k²+(k-1)² si m=3k+1 alors : 3n+1=(3k+1)²<=>3n=9k²+6k <=>n=3k²+2k<=> n+1=k²+k²+(k+1)² CQFD | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 15:11 Jeu 28 Jan 2010, 15:11 | |
| XD j'aurai eu plus de chance si l'écriture Latex avais voulu marché !!
Enfin bon maintenant sa marche en attente du sujet de sylphaen !!
Merci Mohe pour le sujet ^^ | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 16:15 Jeu 28 Jan 2010, 16:15 | |
| voici ma laide solution pour l'inego .... il est clair que les variables jouent un rôle symétriques ainsi on peut supposer que :a≥b≥c (1)si a,b,c≥0 on a donc : b≥b-c<=>b²≥(b-c)² a≥a-c<=>a²≥(a-c)² alors : ^2}+\frac{b^2}{(a-c)^2}+\frac{c^2}{(a-b)^2}\geq%20\frac{a^2}{(b-c)^2}+\frac{b^2}{(a-c)^2}\geq%20\frac{a^2}{b^2}+\frac{b^2}{a^2}\geq2) ------------------------------------------------------------------------------ (2)si a,b,c≤0 on posant: a=-x et b=-y et c=-z (x,y,z>0) on obtient une inégalité équivalente à (1) ..qui est déjà prouvée...... P.S.ça vient de l'homogénéisation car f(a,b,c)=f(-a,-b,-c)  -------------------------------------------------------------------------------------- (3)maintenant si a>0 et b,c<0 l'inégalité est homogène ainsi on peut supposer que a+b+c>0 (car on peut donner à a+b+c une certaine valeur positive) alors on a d'après C.S: ^2}=\sum\frac{a^4}{a^2(b-c)^2}\geq%20\frac{(a^2+b^2+c^2)^2}{\sum%20(ab-ac)^2}) il suffit donc de prouver que : ^2}{\sum%20(ab-ac)^2}\geq%202\Leftrightarrow%20(a^2+b^2+c^2)^2\geq%204(a^2b^2+b^2c^2+c^2a^2-abc(a+b+c))\Leftrightarrow%20(a+b+c)(\sum%20a(a-b)(a-c)+3abc)%20\geq%200) ce qui est vrai car abc>0 et a+b+c>0 et par Schur on a ∑a(a-b)(a-c)≥0 CQFD ------------------------------------------------------------------------------ encore il me reste le cas où a,b>0 et c<0 je reviendrai après incha2llah pour terminer ma solution..... avec cas d'égalité si b=0 et a=-c...or la symétrie des rôles donne encore deux autres cas d'égalité  ..... @+ | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 16:58 Jeu 28 Jan 2010, 16:58 | |
| bSr !
1ére Exo : principe des tiroirs . | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 19:26 Jeu 28 Jan 2010, 19:26 | |
| Pour l'inégo 1 voici ma soluce : Si l'un des variables est nul l'inégalité est trivale .. On suppose que abc≠0 L'inégo équivaut à : 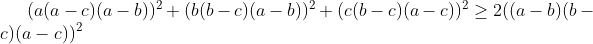 On divise le tous par a²b²c² . L'inégo équivaut à : 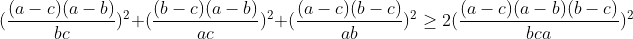 Puis : 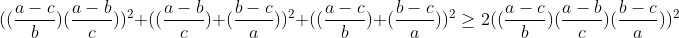 On pose : x=(a-c )/b y=(a-b)/c z=(b-c)/a L'inégo devient : 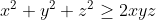 Ce qui équivaut à : x² - x ( 2yz) +y²+z²≥0 En effet le discriminant de l'équation : x² - x ( 2yz) +y²+z²=0 est : Dt= -4( y²+z²-yz)=-4( (y-1/2z)²+3/4z²) ≤0 Donc : Pour tous x de IR on a : x² - x ( 2yz) +y²+z²≥0 CQFD J'avais pas trouvé l'égalité ^^ | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 19:43 Jeu 28 Jan 2010, 19:43 | |
| - Sylphaen a écrit:
- Pour l'inégo 1 voici ma soluce :
Si l'un des variables est nul l'inégalité est trivale ..
On suppose que abc≠0
L'inégo équivaut à :
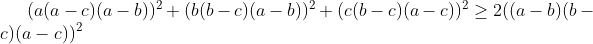 On divise le tous par a²b²c² . On divise le tous par a²b²c² .
L'inégo équivaut à :
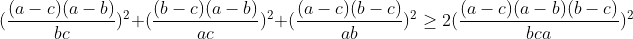 Puis : Puis :
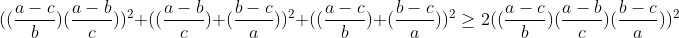 On pose : On pose :
x=(a-c )/b y=(a-b)/c z=(b-c)/a
L'inégo devient :
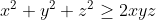
Ce qui équivaut à :
x² - x ( 2yz) +y²+z²≥0
En effet le discriminant de l'équation :
x² - x ( 2yz) +y²+z²=0
est :
Dt= -4( y²+z²-yz)=-4( (y-1/2z)²+3/4z²) ≤0
Donc :
Pour tous x de IR on a : x² - x ( 2yz) +y²+z²≥0
CQFD
J'avais pas trouvé l'égalité ^^ pour ce qui est en gars je crois que c'est x=(a-c )/b.(a-b)/c y=(a-b)/c . (b-c)/a z=(b-c)/a.(a-c )/b et puis je crois que ce qui est en rouge est faux..!!!! car delta=4(y²z²-y²-z²) (P.S.delta= b²-4ac dans une équation du genre ax²+bx+c=0) et non pas ce que tu as trouvé ....ainsi tout en découle faux!!!! c'est pour cela que t'as du prendre 2 / 7 c'est pas pour le cas d'égalité seulement  !!!!!!! | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 19:51 Jeu 28 Jan 2010, 19:51 | |
| Oui je me suis précipité pour le changement de variable
Mais le delta est correcte
car :
4(y²z²-y²-z²)=-4(y²+z²-yz)
?? | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 20:04 Jeu 28 Jan 2010, 20:04 | |
| - Sylphaen a écrit:
- Oui je me suis précipité pour le changement de variable
Mais le delta est correcte
car :
4(y²z²-y²-z²)=-4(y²+z²-yz)
?? 4(y²z²-y²-z²)=-4(y²+z²-yz)<=>4y²z²=4yz<=>yz=0 ou yz=1 crois tu ce que cela est correct!!!!??????  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 28 Jan 2010, 20:11 Jeu 28 Jan 2010, 20:11 | |
| Lol c'était une faute débile dsl ..  | |
|
  | |
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 29 Jan 2010, 07:37 Ven 29 Jan 2010, 07:37 | |
| Bonjour voici ce que j'ai trouvé pour l'inego  DSL je n'est pas completer j'essaye de factoriser la derniere expression | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 29 Jan 2010, 11:34 Ven 29 Jan 2010, 11:34 | |
| joliiiiiii abdelllah pour la dernière tu peux factoriser ainsi : a(a-b)(a-c)+b(b-c)(b-a)+c(c-a)(c-b)=0 mais je crois pas que ça ne peut pas donner grand chose.... mais n'oublie pas qu'en changeant les variables t'as ignoré les cas où a=0 ou b=0 ou c=0 qui présentent également des cas d'égalité  ....
Dernière édition par majdouline le Ven 29 Jan 2010, 14:16, édité 1 fois | |
|
  | |
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 29 Jan 2010, 13:53 Ven 29 Jan 2010, 13:53 | |
| Bonsoir
Merci Majdouline
c'est aussi ce que j'ai fais.Et en essayant d'apliquer SCHUR j'ai trouvé que pas d'egalité si'il sont tous les trois des réels positifs(parce que a#b#c) | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 29 Jan 2010, 15:53 Ven 29 Jan 2010, 15:53 | |
| Pour ne pas allourdir le forum avec bcp de sujets on crée ici toutes les discussions
DISCUSSION pour JOPSM2 proposé par sylphaen | |
|
  | |
regulator
Débutant
 Nombre de messages : 10 Nombre de messages : 10
Age : 30
Localisation : TAZA-Ibn Y
Date d'inscription : 25/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 29 Jan 2010, 20:38 Ven 29 Jan 2010, 20:38 | |
| salut!
par holder
(1+1/x)(1+1/y)(1+1/z)>=(1+1/r.c{1/xyz})^3>=4^3(AM-GM)=64. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 30 Jan 2010, 09:56 Sam 30 Jan 2010, 09:56 | |
| suite aux demandes de quelques forumistes....voici la solution du deuxième sujet  : j'ai pas pu faire le schéma ....j'ai des problème d'hébergement.... exercice 1:1)-soit H le projeté orthogonal de C sur (AB)... en considerant le triangle BCH qui est rectangle en H M le milier de [BC] alors MB=MC=MH ainsi MBH est isocèle en M donc: 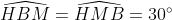 et: 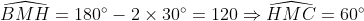 (1) en considérant le triangle AHC qui est rectangle en H on a : 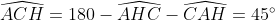 alors ACH est isocèle ==> HC=HA (a)d'autre part on a : 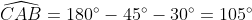 alors: 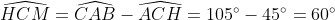 (2) en considérant le triangle HMC et depuis (1) et (2) on a : 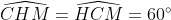 ainsi HCM est équilatéral d'où HM=HC et de (a) on a donc : HM=HA ...alors en considérant le triangle HMA qui est isocèle en H on a : 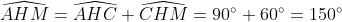 alors : 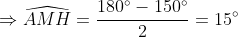 et d'une autre part on a : 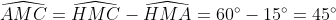 2)-on a donc le deux triangle ABC et AMC sont isocèles car : 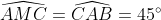 et un angle commun (l'angle C) alors : 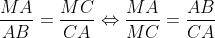 et on a :BC=2MC 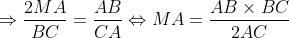 -------------------------------------------------------------------------------- exercice 2:(1+\frac{1}{y})(1+\frac{1}{z})\geq%2064\Leftrightarrow%20(x+1)(y+1)(z+1)\geq%2064xyz\Leftrightarrow%20xy+yz+zx+2\geq%2063xyz) or par Am-Gm on a : ^3}{27}\Leftrightarrow%2054xyz\leq%202) (1) et on a : (\frac{1}{x}+\frac{1}{y}+\frac{1}{z})\geq%209\Leftrightarrow%20xy+yz+zx\geq%209xyz) (2) en sommant (1) et (2) on obtient l'inégalité désirée  ...... exercice3:en remplaçant x par 1-x on a : f[(1-x)²+(1-x)+3]+2f[(1-x)²-3(1-x)+5)=6(1-x)²-10(1-x)+17 <=>f(x²-3x+5)+2f(x²+x+3)=6x²-2x+13 (1) <=>2f(x²-3x+5)+4f(x²+x+3)=12x²-4x+26 (1) et on a : f(x²+x+3)+2f(x²-3x+5)=6x²-10x+17 (2) (1)-(2)=3f(x²+x+3)=6x²+3x+9<=> f(x²+x+3)=2x²+2x+3ainsi il suffit de résourde : x²+x+3=85<=>x²+x-82=0 delta=1+4x82=329 alors : 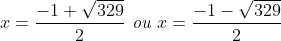 en vérifiant les deux cas on a : =\ 167) | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 30 Jan 2010, 14:12 Sam 30 Jan 2010, 14:12 | |
| Pour le 3éme JOPSM . Exo 1 : On fait la récurrence et on vérifie pour n=3 1=1/2+1/3+1/6 On suppose qu'il existe p entier différent 2à2 tels que : 1/n_1+.....1/n_p=1 Et on montre qu'il existe p+1 entier différent 2à2 tels que : 1/n'_1+....1/n'_p+1=1 On a : 1/n_1+.....1/n_p=1 <=> 1/2( 1/n_1+.....1/n_p)+1/2=1 <=>1/2n_1+....1/2n_p +1/2=1 CQFD Pour le 3 j'ai essayé mais pas terminé ><' Voici ce que j'ai fait L'inégo est homogène car f(a,b,c)=f(ka,kb,kc) On suppose donc que a+b+c=1 L'inégo équivaut à :2( 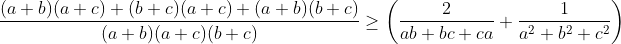 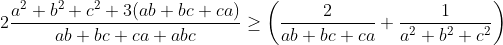 On pose x=a²+b²+c² et y=ab+ac+bc on a x+2y=1 L'inégo équivaut : 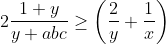 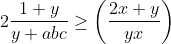 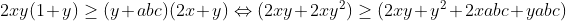 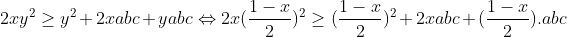 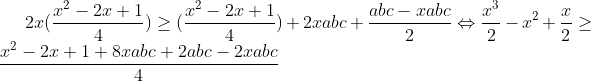 | |
|
  | |
kirua
Expert sup

 Nombre de messages : 647 Nombre de messages : 647
Age : 31
Date d'inscription : 03/10/2008
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 30 Jan 2010, 22:54 Sam 30 Jan 2010, 22:54 | |
| bonsoir
svp c quoi la réponse du jopsm 1 de l exo 1 svp?
merci. | |
|
  | |
regulator
Débutant
 Nombre de messages : 10 Nombre de messages : 10
Age : 30
Localisation : TAZA-Ibn Y
Date d'inscription : 25/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Dim 31 Jan 2010, 10:17 Dim 31 Jan 2010, 10:17 | |
| bonjour voici ma solution pour l inego j espere que ca soit juste... probleme 3: IL suffit de prouver:  puisque (a²+b²+c²>=ab+bc+ac). posant a+c+b=p et ab+bc+ac=q et abc=r...donc l'inegalite est equivalente à:  . on a:  et par AM-GM:  ...  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Dim 31 Jan 2010, 11:34 Dim 31 Jan 2010, 11:34 | |
| bonjour^^ mais je n'arrive pas à comprendre ...si delta>=0 et alors??? ça ne prouve rien...je sais pas mais peut être que tu dois terminer ...pour trouver que f(q)=2q²+3pr-p²q>0 pourtant je propose ceci..... l'inégalité est homogène alors supposer que a+b+c=1....en prenant abc=r et ab+bc+ca=q l'inégalité est donc équivalente à:q²(1-4q)+(2-3q)r≥0 par Schur on a :1-4q≥-9abc alors il suffit de prouver que -9q².r+(2-3q)r≥0 <=>r(1-3q)(2+3q)≥0 ce qui est clairement vrai  | |
|
  | |
regulator
Débutant
 Nombre de messages : 10 Nombre de messages : 10
Age : 30
Localisation : TAZA-Ibn Y
Date d'inscription : 25/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Dim 31 Jan 2010, 12:04 Dim 31 Jan 2010, 12:04 | |
| salut!
donne moi un contre exemple stp car j vois pas ou est la faute! | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Dim 31 Jan 2010, 12:08 Dim 31 Jan 2010, 12:08 | |
| j'ai pas dit que c faux...enfin je peux pas juger...mais ça ne prouve rien ...car le fait de trouver que delta>=0.===>f(q) varie sur IR...positive si q£]-00,q1]U[q2,+00[....et négative si q£[q1,q2]...(avec q1 et q2 les racines de f(q)..........bref:tu dois prouver que q£]-00,q1]U[q2,+00[...ainsi ça sera correct... | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Dim 31 Jan 2010, 22:47 Dim 31 Jan 2010, 22:47 | |
| Je propose ma solution Pour l'exo 3 de JOPSM 4 :
On f(0)= 0 ou f(0)=1 et f(1)=0 ou f(1)=1
Donc f(0)=0 et f(1)=1 car la fonction est strictement croissante
On a clairement :
f(2^n)=f(2)xf(2)...xf(2) nfois = 2^n
f(2^n+1)=2^n+1
Pour tous n>=1 et qui n'est po une puissance de 2 il existe un m tels que
2^m<2^m+1
donc Puisque la fonction est strictement croissante
f(2^m)
2^m
Et donc :
2^m<...<....<2^(m+1)
Puisque la fonction est strictement croissante :
f(2^m+1)≥2^m +1
f(2^m+2)≥2^m + 2>2^m+1
...................................
2^(m+1)>f(2^m -1)≥2^m-1
Donc :
f(2^m-1)=2^m-1
f(2^m-2)=2^m-2
.....................
On conclue que f(n)=n
Pour l'exo 3 on considère le repère orthonormé (C,CD,CA)
Alors les cordonnés des points seront :
A(0,1)
E(V3/2,1/2)
F(1/2,1+V3/2)
Les cordonné des vecteurs :
Vec EA (V3/2,-1/2)
Vec AF (-1/2,-V3/2)
Et par conséquent les 2vecteurs sont colinéaire d'où la conclusions .. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 10:37 Lun 01 Fév 2010, 10:37 | |
| Pour l'exo 2 de Just-Abdess j'ai trouvé que <ABC=45°
Et on a :
D'après les loi de sinus :
Dans ABC
AC/sin<ABC=BC/Sin<CAB
BC=AC. Sin<CAB/SinABC=12 V2. Sin129°=12V2 Cos 39°
Dans ABD
AD/SinABD=BD/sinDAB
AD= BD . SinABD/SinDAB=6V2.cos39° . V2/2 / Sin 51°
On a Sin51=cos(90-51)=cos39
Donc
BD = 6 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  | |
| |
|
  | |
| | Discusion du premier JOPSM; |  |
|
