| | Discusion du premier JOPSM; |  |
|
+14samix just-abdess master reda-t Dijkschneier kirua regulator abdellah=einstein Sylphaen Ayoub M-H darkpseudo majdouline houssam110 MohE 18 participants |
|
| Auteur | Message |
|---|
abdellah=einstein
Maître

 Nombre de messages : 110 Nombre de messages : 110
Age : 31
Localisation : taroudant
Date d'inscription : 07/03/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 11:00 Lun 01 Fév 2010, 11:00 | |
| bonjour voici ce que j'ai trouvé  SVP dans l'ensemble des solutions S={......(m,-m,1);(-m,m,1)} et pas ce qui est sur l'image | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 11:17 Lun 01 Fév 2010, 11:17 | |
| Exercice 2 :Notons 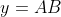 Dans le triangle ADC, la loi des sinus donne : }%20=%20\frac{DC}{\sin(78)}%20=%20\frac{x}{\sin(\hat{C})}) De même dans le triangle ABD : }%20=%20\frac{DC}{\sin(51)}%20=%20\frac{x}{\sin(\hat{B})}) Ainsi, =\sin(\hat{C})\times%20\frac{\sin(51)}{\sin(78)}) Et : \sin(\hat{B})%20=%20\sin(\hat{D_2})\sin(\hat{C})%20\Leftrightarrow%20\frac{1}{12}y\sin(\hat{D_1})=\sin(\hat{D_2})\times\frac{\sin(78)}{\sin(51)})  et  sont supplémentaires, donc %20=%20\sin(180-\hat{D_1})%20=%20\sin(\hat{D_1})) D'où : }{\sin(51)}) Maintenant, il est facile de calculer x. On a d'après le théorème d'Al-Kashi : %20\\%20\Leftrightarrow%20BC^2%20=%20144%20+%20\frac{144\sin^2(78)}{\sin^2(51)}%20-%20\frac{288\sin(78)\cos(129)}{\sin(51)}) Et finalement d'après le théorème de la médiane : }{\sin^2(51)}+\frac{288\sin(78)\cos(129)}{\sin(51)}}{4}%20\\%20\Leftrightarrow%20x%20=%20\frac{\sqrt{144+\frac{144\sin^2(78)}{\sin^2(51)}+\frac{288\sin(78)\cos(129)}{\sin(51)}}}{2}) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 11:25 Lun 01 Fév 2010, 11:25 | |
| Exercice 3 du JOPSM 4 :  | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 11:48 Lun 01 Fév 2010, 11:48 | |
| Salùt ! Probléme 2 du 5éme JOPSM : Soit E le point médian de AB . dessine une ligne ED ED est parallèle à l'AC et égal à 1/2de12 =6 l'angle DEA est le supplément de l'angle A=51 Le triangle DEA est isocèle . de cela : x=6A+!  | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:06 Lun 01 Fév 2010, 12:06 | |
| Pour le Meme Exo , Autre Methode Long :
- Al Kashi dans le triangle ADC:
DC² = x² + 12² - 24x.cos(78)
- Al Kashi dans le triangle ABC:
4.DC² = BC² = AB² + 12² - 24.AB.cos(78+51)
- Al Kashi dans le triangle ABD:
DC² = BD² = AB² + x² - 2.AB.x.cos(51)
------------------------------------------------------------
On arrive au système:
x² + 12² - 24x.cos(78) = AB² + x² - 2.AB.x.cos(51)
4.(x² + 12² - 24x.cos(78)) = AB² + 12² - 24.AB.cos(78+51)
On vas resoudre ce systeme ... j'ai arrivé a :
12² - 24x.cos(78) = [(2x² + 144 - 36x.cos(78))/(x.cos(51) - 12.cos(129))]² - 2.[(2x² + 144 - 36x.cos(78))/(x.cos(51) - 12.cos(129))].x.cos(51)
Equation du 2éme degré qui a une racine double x = 6 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:20 Lun 01 Fév 2010, 12:20 | |
| - Ayoub M-H a écrit:
On vas resoudre ce systeme ... j'ai arrivé a :
12² - 24x.cos(78) = [(2x² + 144 - 36x.cos(78))/(x.cos(51) - 12.cos(129))]² - 2.[(2x² + 144 - 36x.cos(78))/(x.cos(51) - 12.cos(129))].x.cos(51)
Equation du 2éme degré qui a une racine double x = 6 Ça semble plutôt être une équation du quatrième degré, et ses solutions sont toutes complexes.. | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:23 Lun 01 Fév 2010, 12:23 | |
| - Dijkschneier a écrit:
- Exercice 3 du JOPSM 4 :
 Salut dijkschneir la soluiotn ke ta trouvé est : f : IN -{0.1} --> IN-{0.1} n|--> f(n)=n or moi je demandé des solution de IN --> IN donc pour ke la solution soit complete il faut vérifier f(0) et f(1)  | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:31 Lun 01 Fév 2010, 12:31 | |
| - Dijkschneier a écrit:
- Ayoub M-H a écrit:
On vas resoudre ce systeme ... j'ai arrivé a :
12² - 24x.cos(78) = [(2x² + 144 - 36x.cos(78))/(x.cos(51) - 12.cos(129))]² - 2.[(2x² + 144 - 36x.cos(78))/(x.cos(51) - 12.cos(129))].x.cos(51)
Equation du 2éme degré qui a une racine double x = 6 Ça semble plutôt être une équation du quatrième degré, et ses solutions sont toutes complexes.. Vraiment je n'ai pas meme contunier .. d'aprés Ma premier Solution j'ai trouvé x=6 .. de cela j'ai cru que c'est la seule solution de l'equation vu que tout ce qui est avant est juste ... je vais encore esseyé ... | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:31 Lun 01 Fév 2010, 12:31 | |
| - houssam110 a écrit:
Salut dijkschneir
la soluiotn ke ta trouvé est :
f : IN -{0.1} --> IN-{0.1}
n|--> f(n)=n
or moi je demandé des solution de IN --> IN
donc pour ke la solution soit complete
il faut vérifier f(0) et f(1)  Bien vu ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:34 Lun 01 Fév 2010, 12:34 | |
| - Ayoub M-H a écrit:
Vraiment je n'ai pas meme contunier .. d'aprés Ma premier Solution j'ai trouvé x=6 .. de cela j'ai cru que c'est la seule solution de l'equation vu que tout ce qui est avant est juste ... je vais encore esseyé ... J'avais essayé également de résoudre le problème uniquement à dose d'Al-Kashi, mais je n'avais pas réussi. Il fallait faire intervenir d'autres subtilités. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 01 Fév 2010, 12:43 Lun 01 Fév 2010, 12:43 | |
| Exo 1 :
x+y+z=1
Et :
x³+y³=1-z²
(x+y)(x²+y²-xy)=(1-z)(1+z)
(1-z)(x²+y²-xy-(1+z))=0
1-z=0 ou (x²+y²-xy-(1+z))=0
si z=1 alors x=-y
S_1={(n,-n,1)/n£ZI}
Si
(x²+y²-xy-(1+z))=0
on a :
(x²+y²-xy-(1+z)) =0 x²+y²-xy -( 2-x-y)=0
x²+y²-xy+x+y-2=0
2x²+-2xy+4x+2y²+4y=4
(x-y)²+(x+1)²+(y+1)²=6
|y+1|≤2 car y£ZI
Donc -3≤y≤1 => y£{-3,-2,-1,0,1}
Si :
y=1 =>(x-1)²+(x+1)²=2=>x=0 et z=0
Si :
y=0=>x²+(x+1)²=5=>x=1 ou x=-2 => (x=1 et z=0) ou (x=-2 et z=3)
Si y=-1=>2(x+1)²=6=> x+1=V3 absurde
Si :
y=-2 =>(x+2)²+(x+1)²=5=>x=0 ou x=-3 => (x=0 et z=3)ou(x=-3et z=6)
Si :
y=-3=>(x+3)²+(x+1)²=2 => x=-2 et z=6
On trouve les même couple avec y donc :
S={(1,0,0),(0,1,0),(-2,0,3),(0,-2,3),(-3,-2,6),(-2,-3,6),(n,-n,1)/n£ZI} | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mar 02 Fév 2010, 08:42 Mar 02 Fév 2010, 08:42 | |
| j'étais pas là...ainsi je n'ai pas pas pu participé au récent sujet...je vois que vous avez posté assez de bonnes solution aux problèmes 1 et 2...donc voici ce que je propose pour l'inégalité de l'exo3 : par Am-Gm on a:     ce qui équivaut à:  Or par Am-Gm on a :  CQFD avec égalité si et seulement si :  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mar 02 Fév 2010, 10:30 Mar 02 Fév 2010, 10:30 | |
| malheureusement je n'ai pas pu participé car j'étais pas là...et pourtant je vous propose ma solution pour ce joli sujet....... Exo1:Df=[0,a²]  ^2=(\sqrt{a-\sqrt{x}}-\frac{1}{2})^2)   ^2=a-\sqrt{x})   alors si a≥1 ^2}{4},\frac{(1+\sqrt{4a-3})^2}{4}%20\right%20\}\cap%20Df) si 1≥a≥3/4 on a donc : ^2}{4},\frac{(1-\sqrt{4a-3})^2}{4},\frac{(1+\sqrt{4a-3})^2}{4}%20\right%20\}\cap%20Df) si 3/4≥a alors: ^2}{4}%20\right%20\}\cap%20Df) --------------------------------------------------------------------------------------- Exo2....on a f(xf(y))=f(xy)+x pour y=1/x on a : )=f(1)+x) pour x=-f(1) on a donc : (∃b£IR):f(b)=0 alors pour y=b et x=1 on a donc : f(f(b))=f(b)+1 <=>f(0)=1 alors pour y=0 on a : (∀x£IR):f(x.f(0))=f(0)+x <=>(∀x£IR) f(x)=1+x inversement... effectivement,cette solution vérifie l'équation fonctionnelle donnée  ........ Exo3:donc notons:  donc en prenant: a+2b+c=x et a+b+2c=y et a+b+3c=z on aura:   or par Am-Gm on a :  alors : min=12V2-17 P.S.abdellah;très bon choix d'exos 
Dernière édition par majdouline le Mar 02 Fév 2010, 13:01, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mar 02 Fév 2010, 12:56 Mar 02 Fév 2010, 12:56 | |
| Juste un petite faute de frappe pour l'exo 3 :
z=a+b+3c ^^ | |
|
  | |
regulator
Débutant
 Nombre de messages : 10 Nombre de messages : 10
Age : 30
Localisation : TAZA-Ibn Y
Date d'inscription : 25/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mar 02 Fév 2010, 14:20 Mar 02 Fév 2010, 14:20 | |
| bonjour...
bravo majdouline...mais je pense que pour l exo 3 c pas terminer tu dois indiquer le cas d'egalite...si il existe a_0;b_0;c_0: tq
f(a_0;b_0;c_0)=12sqrt(2)-17...si nn good job^^.
et pour l exo 2 j propose une autre solution^^:
f(xf(y))=f(xy)+x.
-si f(0)=0:
(x;f(0))===>f(xf(0))=f(0)+x<==>x=0!!!!!
donc f(0)#0!
posant: f(0)=c ou c est une constante reel alors:
(x;0)===> f(xc)=x+c. ==>f(x)=x/c+c...on verifie dans la premiere equation et on trouve que c=1..
(for all(x)£IR) : f(x)=x+1. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mar 02 Fév 2010, 15:10 Mar 02 Fév 2010, 15:10 | |
| oui...c vrai,je dois indiquer un cas d'égalité...par exemple: =(5\sqrt{2}-7,3-2\sqrt{2},2-\sqrt{2})) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 12:06 Mer 03 Fév 2010, 12:06 | |
| je crois qu'il te manque une solution {1}!! à propos, je ne veux en aucun cas critiquer ayoub mais puis-je savoir pourquoi je n'ai eu que 6 points pour cet exo: est ce que j'ai fait une erreur? si oui laquelle ? amicalement!  
Dernière édition par reda-t le Mer 03 Fév 2010, 12:10, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 12:07 Mer 03 Fév 2010, 12:07 | |
| Solution de l'exo 1 :    Posons : 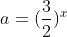 L'équation équivaut à : a + 1/a = 13/6 En calculant les racine on trouve que : a=3/2 ou a=2/3 i.e x=1 ou x=-1 S={-1,1} | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 12:21 Mer 03 Fév 2010, 12:21 | |
| - reda-t a écrit:
- je crois qu'il te manque une solution {1}!! à propos, je ne veux en aucun cas critiquer ayoub mais puis-je savoir pourquoi je n'ai eu que 6 points pour cet exo: est ce que j'ai fait une erreur? si oui laquelle ?
amicalement!   Meme parmis les regles du jeu de ne pas discuter la correction .. Ta Solution étais bien juste ... but avec une ecrirure pas bien claire & aprés avoir terminer la periode du sujet (22h) ... Merci pour votre compréhension ... A+!  | |
|
  | |
reda-t
Maître
 Nombre de messages : 127 Nombre de messages : 127
Age : 31
Localisation : latitude: 34°01'31'' nord
Date d'inscription : 19/08/2009
 | |
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 12:32 Mer 03 Fév 2010, 12:32 | |
| Non Comme j'ais dit Ta Solution est bien juste .. Ya pas de bléms, essaie d'ecrire en Latexe & a l'heur  | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 17:35 Mer 03 Fév 2010, 17:35 | |
| moi meme houssam110 ma donne que point pour les deux exo du JOPSM5 a cause ma mauvaise ecriture ....... | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 19:56 Mer 03 Fév 2010, 19:56 | |
| Bonjour!
Si vous lisez bien les règles du jeux, vous saurais qu'on ne donne 7 points que pour une solution, complète , corrècte et élègante. d'une autre part, je ne pourrais plus participer, car j'ai des problems avec mon Pc, que j'essaie de réparer. D'ailleurs, je veux bien proposer des notes pour quelques problèmes deja proposé:
Jopsm1, Problèmes 1:
supposons le contraire, soit A et B deux points dans le carré, sans pertes de généralité supposons que A et noir, B est Blanc,
-Soit C(A,1) le cercle de centre A et de rayon 1
=> tout les points du cercle C doivent être blanche.
-Soit C'(B,1) le cercle de centre B et de rayon 1
=> tout les points du cercle C' doivent être noire.
Or ceci est absurde car les cercles C et C' s'intersectent au moins dans un point qui ne pourrais -bien sur- pas être noir et blanc à la fois.
Jopsm1, Problème 2:
il suffit de poser a-b=x, b-c=y et c-a=z, l'inégalité equivaut alors à:
a²z²y²+b²x²z²+c²x²y²>=2x²y²z²
<=> (azy+bxz+cxy)²-2xyz(abz+bcx+acy+xyz)>=0
il ne vous reste que prouver que:
abz+bcx+acy+xyz=0 qui est facile
le cas d'égalité est lorsque:
a(a-b)(a-c)+b(b-c)(b-a)+c(c-a)(c-b)=0
P.S: l'inegalité de shur est pour les réels positifs.
Jopsm2:
très joli, j'ai des deja envoyé mes solution a l'auteur, je l'ai reposterai ulterieurement.
Jopsm3, problem 2:
Je crois qu'il faut ajouter a l'ennoncé que 4n+1 n'est pas un carré parfait, toutefois, il ne faut pas oublier dans la solution (que je vois facile) de prouver que 4n+2 et 4n+3 ne sont jamais des carrés parfait (trivial).
Jopsm4, Problem 3:
j'ai bcp aimer ce problème, a vous de commenter ma solution  : n=m => f(n²)=[f(n)] ² n=0 et m=2 =>f(0)=0
n=1 et m=2 => f(1)=1
après j'ai prouver que n-1
pour f(n)>n-1.
supposons le contraire alors pour un entier a on a f(a)=f(a-1)>...>f(0) on déduit que les entiers f(0),...,f(a) £{0,1,...,a-1}=E
Or E ne contient que a élèment d'ou et d'après le principe des tiroirs il existe au moins i et j £{0;...;a} tels que i>j et avec f(i)=f(j) ce qui est impossible du fait que f est strictement croissante. d'ou f(n)>n-1
Pour f(n)<n+1
pour 0,1,2 ca marche, soir a>=2 on suppose que f(a)<a+1
f(a²)>f(a²-1)=f(a+1)f(a-1)
=> f(a+1)<[f(a)]²/f(a-1)=<a²/a-1=<a-2 ==> f(a+1)<a+2
=> n-1<f(n)<n+1 => f(n)=n, et ainsi, j'ai prouver aussi que c'est la seule solution.
Jopsm 7, Problem 2:(a+b+1)(a+b+c²)>=(a+b+c)²
=> 1/(a+b+1) =< (a+b+c²)/(a+b+c)²
de même pour les autre et on trouve que,
[2(a+b+c)+(a²+b²+c²)]/(a+b+c)²>=1
=> a+b+c >= ab+bc+ca.
Jopsm 7, Problem 3:
la loi des sinus fait deja l'affaire!
Jopsm 8,Problem 3:
c'est vraie que le problems est très jolie, mais il ne merite pas d'être un problem 3, avec tout respect. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 20:52 Mer 03 Fév 2010, 20:52 | |
| te de ma part je poste une autre solution pour l'inégalité du récent Jopsm.... donc notons : a+b=x,b+c=y c+a=z alors :  -x^2-y^2-z^2}{4}) la condition devient:  et l'inégalité équivalente à : ^2+2(x+y+z)\geq%204(xy+yz+zx)) par Shur ..il suffit donc de prouver que : \geq%20\frac{9xyz}{x+y+z}\Leftrightarrow%202(x+y+z)^2\geq%209xyz) si xyz≤8 si xyz≤8 alors :  CQFD ------------------------------------------------------------------------------------ si xyz≥8....on doit prouver que: \geq%20\frac{9xyz}{x+y+z}\Leftrightarrow%202(x+y+z)^2\geq%209xyz) on a:  alors il suffit de prouver que:  ce qui est clairement vrai.................... sauf erreur ...........
Dernière édition par majdouline le Jeu 04 Fév 2010, 09:53, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  | |
| |
|
  | |
| | Discusion du premier JOPSM; |  |
|
