| | Discusion du premier JOPSM; |  |
|
+14samix just-abdess master reda-t Dijkschneier kirua regulator abdellah=einstein Sylphaen Ayoub M-H darkpseudo majdouline houssam110 MohE 18 participants |
|
| Auteur | Message |
|---|
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Mer 03 Fév 2010, 22:26 Mer 03 Fév 2010, 22:26 | |
| - MohE a écrit:
Jopsm 8,Problem 3:
c'est vraie que le problems est très jolie, mais il ne merite pas d'être un problem 3, avec tout respect. Salut Oui , tu as raison , il fallait que je le met au premier , mais moi sans faire attention j'ai fais probleme 1 difficile probleme 2 moyen probleme 3 facile | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 09:33 Jeu 04 Fév 2010, 09:33 | |
| salut tt le monde
salut mohe
pur JOPSM 3
4n+1 peu etre un carré parfait
or c 4n+2 et 4n+3 ki ne peuvent po etre ds carrés parfaits ckyé démontrable..
et voici ma solution
https://2img.net/r/ihimizer/img22/6324/problem2n.png
A+ | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 22:59 Jeu 04 Fév 2010, 22:59 | |
| mes solutions proposées aux 8ème JOPSM.....Exo1: on a x et y ont donc le même signe car x 3y est positif et puisque la somme 3x+y est positive alors x,y sont positifs ...ainsi en appliquant Am-Gm on a :   impossible on a donc: S={ma localisation} ----------------------------------------------------------------------------------------- Exo 2: notons :  en considérant le triangle ADB en en appliquant la loi des sinus on a :  =sin(60-\alpha%20))   or en considérant le triangle ADC on a :   alors :    re^^ cette équation admet comme solution:  d'après Pythagore on a donc :  ------------------------------------------------------------------------ problème3: notre inégalité est équivalente à: \geq%20a+b+c+6) notons a+1=x b+1=y et c+1=z ainsi l'inégalité devient: \geq%203(x+y+z)) or par Cauchy Schwartz on a:  et on a : ^2}{3}) alors il suffit de démontrer que : ^2}{3}+\frac{36}{x+y+z}\geq%203(x+y+z)) ^3-9(x+y+z)^2+108\geq%200) ^2(x+y+z+3)\geq%200) ce qui est clairement vrai... done!! joli sujet samix^^
Dernière édition par majdouline le Ven 05 Fév 2010, 12:11, édité 4 fois | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 23:11 Jeu 04 Fév 2010, 23:11 | |
| merci d'avoir aimé le sujet majdouline
mais en ce qui concerne ta solution pour l'inégalité je pense que t'as fais une faute de frappe dans la 5ème ligne c'est plûtot 3(x+y+z) et non pas x+y+z | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 23:15 Jeu 04 Fév 2010, 23:15 | |
| oui merci samix c'est corrigé..... | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 23:22 Jeu 04 Fév 2010, 23:22 | |
| Solution de l'exo 3 : On a :  L'inégo équivaut donc à :  Or que : a²+1 >= 2a Donc :  Il suffit de prouve donc que :  Posons : a+1=x b+1=y c+1=z L'inégo équivaut à :  Par IAG on a : x + 4/x >= 2V(x.4/x)=4 Donc :  CQFD  | |
|
  | |
La volonté
Maître
 Nombre de messages : 115 Nombre de messages : 115
Age : 31
Date d'inscription : 15/05/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 23:26 Jeu 04 Fév 2010, 23:26 | |
| | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Jeu 04 Fév 2010, 23:33 Jeu 04 Fév 2010, 23:33 | |
| Salùt !  A+!  | |
|
  | |
Ayoub M-H
Maître
 Nombre de messages : 111 Nombre de messages : 111
Age : 31
Date d'inscription : 08/04/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 05 Fév 2010, 01:25 Ven 05 Fév 2010, 01:25 | |
| Pour le 1ére Exo la présentation Graphique véréfie aussi le resultat trouvé :  A+!  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Ven 05 Fév 2010, 09:52 Ven 05 Fév 2010, 09:52 | |
| Le graph est plutôt ainsi :  Y ne prend jamais 0 comme valeurs .. mais bons je pense que la solution de Majdouline était la meilleure =) | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 06 Fév 2010, 15:05 Sam 06 Fév 2010, 15:05 | |
| 10ème JOPSM :Exercice 2 :On considère la suite _{n\in%20\mathbb{N}}) définie par  On peut alors facilement prouver que c'est une suite de Fibonacci généralisée (  ) Par récurrence, on peut prouver que notre suite appartient à  , puis qu'elle est strictement croissante dans  Nommons E l'ensemble défini par %20\}) Et considérons la proposition %20:%20(\forall%20m%20\in%20\mathbb{N^*}%20-%20\{1\},%20\:%20m%3Cu_n)%20\%20m\in%20E) ) est vraie car le seul entier inférieur à 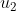 (3) et qui appartient à  est 2, et 2 appartient à  (  ) Montrons que &space;\Rightarrow&space;P(n+1)) : On a %20&\Rightarrow%20P(n) \text{ et } P(n-1)%20\:%20\text%20{%20et%20}%20\:%20(\forall%20m\in%20\mathbb{N^*}%20-%20\{1\},%20m%3Cu_{n-1})%20\text%20{%20m%20ne%20contient%20pas%20}%20u_n%20\text{%20dans%20son%20\%27ecriture}%20\\%20&\Rightarrow%20(\forall%20m\in%20\mathbb{N^*}%20-%20\{1\},%20m%3Cu_{n-1}+u_{n})%20\%20m\in%20E%20\\%20&\Rightarrow%20(\forall%20m\in%20\mathbb{N^*}%20-%20\{1\},%20m%3Cu_{n+1})%20\%20m\in%20E%20\\%20&\Rightarrow%20P(n+1)%20\end{align*}) Finalement, ) est vraie pour tout 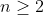 Et puisque  , alors %20\%20m\in%20E) Aussi, on peut vérifier que 1 appartient à E. Donc  CQFD.
Dernière édition par Dijkschneier le Sam 07 Aoû 2010, 21:52, édité 2 fois | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 06 Fév 2010, 15:32 Sam 06 Fév 2010, 15:32 | |
| Euh pour un peu d'eclaircissement :
Que représente exactement la propriété P(n) ? | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 06 Fév 2010, 15:46 Sam 06 Fév 2010, 15:46 | |
| Juste un petit eclairessissement , le nombre avec lequel on travail n'est il pas le nombre d'or ?? si oui alors tout les nombre appartiennent a la suite de fibonnaci et la question est déja vérifié !!
Merci de me répondre ^^ | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 06 Fév 2010, 16:16 Sam 06 Fév 2010, 16:16 | |
| - darkpseudo a écrit:
- Juste un petit eclairessissement , le nombre avec lequel on travail n'est il pas le nombre d'or ??
Tout à fait.  est le nombre d'or. - darkpseudo a écrit:
- si oui alors tout les nombre appartiennent a la suite de fibonnaci et la question est déja vérifié !!
Quelle question ? Il s'agit ici de prouver que tous les entiers naturels non nuls peuvent s'écrire d'une manière unique (à l'ordre de la commutativité de l'addition près), comme une somme de puissances distinctes de  et de 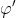 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 06 Fév 2010, 16:23 Sam 06 Fév 2010, 16:23 | |
| Oui c'est ce que je voulais savoir merci ^^' | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Sam 06 Fév 2010, 16:51 Sam 06 Fév 2010, 16:51 | |
| - Othmaann a écrit:
- Euh pour un peu d'eclaircissement :
Que représente exactement la propriété P(n) ? Il serait violent si l'on tentait de traduire verbalement la signification de P(n), et ça ne serait pas non plus tentant à connaître. Je vais donc me borner à l'explication suivante : L'objectif de l'exercice était de prouver que %20\%20m\in%20E) était vraie. Mais cette proposition n'est pas facile à appréhender. On a donc introduit la proposition P(n), qui est plus "faible", mais plus facile à démontrer. Ensuite, de la véracité de P(n), on en a déduit celle de %20\%20m\in%20E) . La proposition P(n) n'était finalement qu'une passerelle.
Dernière édition par Dijkschneier le Mer 14 Juil 2010, 18:35, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 | |
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 08 Fév 2010, 15:56 Lun 08 Fév 2010, 15:56 | |
| JOPSM 11:
exo 3 :
d'apres l'IAG on aura : a^5+b^5+ab>= 3(ab)²>=3ab
alors ab/a^5+b^5+ab =< 1/3 (*)
donc bc/b^5+c^5+bc=< 1/3 (**)
et ac/a^5+c^5+ac =< 1/3 (***)
en sommant (*)et (**) et (***) on trouveras que :
ab/a^5+b^5+ab + bc/b^5+c^5+bc + ac/a^5+c^5+ac =<1/3+1/3+1/3=1 | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 08 Fév 2010, 16:19 Lun 08 Fév 2010, 16:19 | |
| deuxieme methode:
a^5+b^5 = (a+b)((a-b)(a^3-b^3)+a²b²)>= (a+b)(ab)²
donc ab/a^5+b^5+ab =< ab/(a+b)a²b²+ab = c/a+b+c
avec la meme facon on vas distinguer les autres inegalite pour avoir que : ab/a^5+b^5+ab + bc/b^5+c^5+bc + ac/a^5+c^5+ac =< c/a+b+c +a/a+c+b + b/a+c+b =a+b+c/a+b+c = 1
d'ou la conclusion ... | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 08 Fév 2010, 17:07 Lun 08 Fév 2010, 17:07 | |
| - master a écrit:
- JOPSM 11:
d'apres l'IAG on aura : a^5+b^5+ab>= 3(ab)²>=3ab
Pourquoi ? | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 08 Fév 2010, 17:31 Lun 08 Fév 2010, 17:31 | |
| d'apres IAG a^5+b^+ab >= 3(a^5.b^5.ab)^1/3=3((ab)^6)^1/3 = 3(ab)^6/3=3(ab)²
puisque on a (ab)²>=ab alors en pultipliant avec 3 :
3(ab)²>= 3ab | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 08 Fév 2010, 17:44 Lun 08 Fév 2010, 17:44 | |
| - master a écrit:
- d'apres IAG a^5+b^+ab >= 3(a^5.b^5.ab)^1/3=3((ab)^6)^1/3 = 3(ab)^6/3=3(ab)²
puisque on a (ab)²>=ab alors en pultipliant avec 3 :
3(ab)²>= 3ab 3(ab)²>= 3ab est juste si et seulement ab >= 1 | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  Lun 08 Fév 2010, 18:18 Lun 08 Fév 2010, 18:18 | |
| mais si on donne que ab=0 0=<0 ce qui est vrais ????? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Discusion du premier JOPSM; Sujet: Re: Discusion du premier JOPSM;  | |
| |
|
  | |
| | Discusion du premier JOPSM; |  |
|
