| | UN SUJET: Limites compliqués |  |
|
+4Oeil_de_Lynx kobica Pedro thunder bazzou 8 participants |
|
| Auteur | Message |
|---|
bazzou
Féru
 Nombre de messages : 35 Nombre de messages : 35
Age : 31
Date d'inscription : 14/10/2009
 |  Sujet: UN SUJET: Limites compliqués Sujet: UN SUJET: Limites compliqués  Mar 16 Mar 2010, 12:17 Mar 16 Mar 2010, 12:17 | |
| Salam alaykoum ici je vais poster des limites surtout le type général de n premier limite:  pour moi j'ai les réponses, juste c'est pour vous! alors je veut pas le genre de posts (tu va utilisé ...) si tu veux partagé ta réponse Mrhba si nn chrché un autre sujet! | |
|
  | |
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 | |
  | |
Pedro thunder
Habitué

 Nombre de messages : 18 Nombre de messages : 18
Age : 31
Date d'inscription : 01/12/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Jeu 18 Mar 2010, 20:48 Jeu 18 Mar 2010, 20:48 | |
|
Dernière édition par Pedro thunder le Ven 19 Mar 2010, 13:16, édité 1 fois | |
|
  | |
kobica
Maître

 Nombre de messages : 74 Nombre de messages : 74
Age : 31
Date d'inscription : 29/04/2008
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Jeu 18 Mar 2010, 21:17 Jeu 18 Mar 2010, 21:17 | |
| salut bazzou
pour ta question c'est juste savoir lim qd x-->0 de (1-cosx)/x²
on a
(1) 1-cos(x)*cos²(x)*..;cos^n(x)=1-cos^(n(n+1)/2)(x)
=(1-cos(x))(sigma(k=0-->n(n+1)/2-1)cos^k(x))
et on a lim(1-cos(x))/x²)=1/2
alors lim(1)/x²=1/2*n(n+1)/2 =n(n+1)/4
done | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Ven 19 Mar 2010, 08:37 Ven 19 Mar 2010, 08:37 | |
| BJR Pedro thunder !! J'ai une petite observation à faire concernant ta réponse ci-dessus ...... Tu as tout à fait le Droit de remplacer x par 2x .... MAIS tu ne peux pas écrire : Lim f(x) = Limf(2x) lorsque x -----> 0 SAUF si tu justifies par un autre procédé que la première Limite existe bien ...... Ce type d'erreur a été commis il n'y a pas longtemps au sujet d'une autre limite ICI même : https://mathsmaroc.jeun.fr/premiere-f5/limite-complique-t15640.htm#132256LHASSANE | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 13:03 Sam 20 Mar 2010, 13:03 | |
| Salut, Cos^2(x)Cos^3(x)...Cos^n(x)}{x^2}%20=%20\lim_{x\to%200}\frac{1-Cos^{(1+2+3+4...+n)}(x)}{x^2}%20=%20\lim_{x\to%200}\frac{1-Cos^{\frac{n(n+1)}{2}}(x)}{x^2}%20=%20\lim_{x\to%200}\frac{(1-Cos(x))(Cos^{\frac{n(n+1)}{2}-1}(x)%20+%20Cos^{\frac{n(n+1)}{2}-2}(x)%20+%20Cos^{\frac{n(n+1)}{2}-3}(x)%20...+%20Cos^(x)+1)}{x^2}%20=%20\frac{1}{2}\cdot%20\frac{n(n+1)}{2}%20=%20\frac{n(n+1)}{4}) On peut aussi le démontrer par récurrence ou bien avec l'Hôpital ou encore avec une autre méthode un peu tirée par les cheveux en ajoutant et en soustrayant Cos(x) dans le numérateur et en factorisant puis en utilisant la même méthode à plusieurs reprises. Voilà. Au plaisir. | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 15:57 Sam 20 Mar 2010, 15:57 | |
| BJR à Toutes et Tous !!
En fait kobika , puis mizmaz ont répondu CORRECTEMENT à la question !! Cependant , je me pose la question suivante :
et si on changait la fonction dont on cherche la LIMITE lorsque x tend vers ZERO ainsi :
f(x)=N(x)/D(x) avec
N(x)=1 - COS(x).COS(2x).COS(3x).......... COS(nx)
et D(x)=x^2
Cette LIMITE est dans Al-Moufid BACSM ( Terminales ) .....
Bonne Chance et Excusez mon intrusion .....
LHASSANE | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 21:33 Sam 20 Mar 2010, 21:33 | |
| - Oeil_de_Lynx a écrit:
- BJR à Toutes et Tous !!
En fait kobika , puis mizmaz ont répondu CORRECTEMENT à la question !! Cependant , je me pose la question suivante :
et si on changait la fonction dont on cherche la LIMITE lorsque x tend vers ZERO ainsi :
f(x)=N(x)/D(x) avec
N(x)=1 - COS(x).COS(2x).COS(3x).......... COS(nx)
et D(x)=x^2
Cette LIMITE est dans Al-Moufid BACSM ( Terminales ) .....
Bonne Chance et Excusez mon intrusion .....
LHASSANE Bah oui, et tu utilises la règle de l'Hôpital par la suite.  | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 21:49 Sam 20 Mar 2010, 21:49 | |
| Autre limite du même type, mais plus corsée : cos(2x)...cos(nx)}{x^2}) | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 | |
  | |
kobica
Maître

 Nombre de messages : 74 Nombre de messages : 74
Age : 31
Date d'inscription : 29/04/2008
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 22:23 Sam 20 Mar 2010, 22:23 | |
| salut Oeil_de_Lynx
on a (1) 1-COS(x)COS(2x)..COS(nx)
=(1-COS(x))+COS(x)(1-COS(2x))+COS(x)COS(2x)(1-COS(3x))
+...(COS(x)..COS((n-1)x))(1-COS(nx))
donc lim (1)/x²=1/2 +1/2*4+...+1/2*n²=1/2*n(n+1)(2n+1)/6
=n(n+1)(2n+1)/12
done | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 23:04 Sam 20 Mar 2010, 23:04 | |
| BSR kobica !!
Oui tout à fait Juste !! BRAVO !
Détaillez un peu plus les étapes ....
LHASSANE | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 23:19 Sam 20 Mar 2010, 23:19 | |
| - oussama1305 a écrit:
- Autre limite du même type, mais plus corsée :
cos(2x)...cos(nx)}{x^2}) On peut aussi soupçonner le résultat après avoir développé un peu la limite puis le confirmer par récurrence. (Pour développer : Cos(2x)Cos(3x)...Cos(nx)}{x^2}%20=%20\lim_{x\to%200}\frac{1-Cos(x)Cos(2x)Cos(3x)...Cos(nx)%20+%20Cos(x)%20-%20Cos(x)}{x^2}%20=%20\lim_{x\to%200}\frac{1%20-%20Cos(x)+%20Cos(x)(1-Cos(2x)Cos(3x)...Cos(nx))}{x^2}%20=%20\lim_{x\to%200}\frac{1%20-%20Cos(x)+%20Cos(x)(1-%20Cos(2x)%20+%20Cos(2x)(1-Cos(3x)...Cos(nx)))}{x^2}%20=%20\frac{1^2}{2}%20+%20\frac{2^2}{2}%20+%20\frac{3^2}{2}%20+%20...%20+%20\frac{n^2}{2}%20=%20\frac{1^2%20+%202^2%20+%203^2%20+%20...%20+%20n^2}{2}%20=%20\frac{\frac{n(n+1)(2n+1)}{6}}{2}%20=%20\frac{n(n+1)(2n+1)}{12}) ) | |
|
  | |
Oeil_de_Lynx
Expert sup

 Nombre de messages : 3113 Nombre de messages : 3113
Age : 76
Localisation :
Date d'inscription : 13/08/2007
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Sam 20 Mar 2010, 23:41 Sam 20 Mar 2010, 23:41 | |
| Re-BSR à Vous !!!
Je vois que oussama1305 a reposé la même LIMITE que celle que j'ai proposée auparavant .........
Je vous suggère de procéder ainsi :
1) Montrer par récurrence sur n >=1 que la LIMITE en question existe ; on l'appellera An puisqu'elle dépend de n seul ....
2) En même temps et en écrivant :
1-cos(x).cos(2x) ...... cos((n+1).x)
=1-cos(n+1)x) + cos((n+1)x).{1-cosx.cos(2x) ..... cos(nx)}
établir que l'on a A(n+1)=(1/2).(n+1)^2 + An
3) En déduire alors l'expression :
An=(1/2).{1^2 + 2^2 + 3^2 + ..... + n^2}=.......
LHASSANE | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 09:33 Dim 21 Mar 2010, 09:33 | |
| - Oeil_de_Lynx a écrit:
- Re-BSR à Vous !!!
Je vois que oussama1305 a reposé la même LIMITE que celle que j'ai proposée auparavant .........
Je vous suggère de procéder ainsi :
1) Montrer par récurrence sur n >=1 que la LIMITE en question existe ; on l'appellera An puisqu'elle dépend de n seul ....
2) En même temps et en écrivant :
1-cos(x).cos(2x) ...... cos((n+1).x)
=1-cos(n+1)x) + cos((n+1)x).{1-cosx.cos(2x) ..... cos(nx)}
établir que l'on a A(n+1)=(1/2).(n+1)^2 + An
3) En déduire alors l'expression :
An=(1/2).{1^2 + 2^2 + 3^2 + ..... + n^2}=.......
LHASSANE Oui, voilà, c'est tout-à-fait ce à quoi j'ai pensé.  | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 10:19 Dim 21 Mar 2010, 10:19 | |
| - Oeil_de_Lynx a écrit:
- Re-BSR à Vous !!!
Je vois que oussama1305 a reposé la même LIMITE que celle que j'ai proposée auparavant .........
Je vous suggère de procéder ainsi :
1) Montrer par récurrence sur n >=1 que la LIMITE en question existe ; on l'appellera An puisqu'elle dépend de n seul ....
2) En même temps et en écrivant :
1-cos(x).cos(2x) ...... cos((n+1).x)
=1-cos(n+1)x) + cos((n+1)x).{1-cosx.cos(2x) ..... cos(nx)}
établir que l'on a A(n+1)=(1/2).(n+1)^2 + An
3) En déduire alors l'expression :
An=(1/2).{1^2 + 2^2 + 3^2 + ..... + n^2}=.......
LHASSANE Excusez le petit malentendu, j'étais un peu fatigué hier  Pour me repulper, une autre très facile  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 10:33 Dim 21 Mar 2010, 10:33 | |
| - oussama1305 a écrit:
- Oeil_de_Lynx a écrit:
- Re-BSR à Vous !!!
Je vois que oussama1305 a reposé la même LIMITE que celle que j'ai proposée auparavant .........
Je vous suggère de procéder ainsi :
1) Montrer par récurrence sur n >=1 que la LIMITE en question existe ; on l'appellera An puisqu'elle dépend de n seul ....
2) En même temps et en écrivant :
1-cos(x).cos(2x) ...... cos((n+1).x)
=1-cos(n+1)x) + cos((n+1)x).{1-cosx.cos(2x) ..... cos(nx)}
établir que l'on a A(n+1)=(1/2).(n+1)^2 + An
3) En déduire alors l'expression :
An=(1/2).{1^2 + 2^2 + 3^2 + ..... + n^2}=.......
LHASSANE Excusez le petit malentendu, j'étais un peu fatigué hier 
Pour me repulper, une autre très facile (\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x})}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}%20=%20\lim_{x\to%20+oo}\frac{x+\sqrt{x+\sqrt{x}}-x}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}=\lim_{x\to%20+oo}\frac{\sqrt{x}\sqrt{1+\frac{1}{\sqrt{x}}}}{\sqrt{x}(\sqrt{1+\sqrt{\frac{1}{x^2}+\frac{1}{x\sqrt{x}}}}+1)}=\frac{1}{2}) Sauf erreur. xD Au plaisir ! Edit : Corrigé.
Dernière édition par mizmaz le Dim 21 Mar 2010, 10:55, édité 2 fois | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 10:34 Dim 21 Mar 2010, 10:34 | |
| Regarde le passage de la troisième à la quatrième étape, t'a oublié un +1. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 10:36 Dim 21 Mar 2010, 10:36 | |
| Ah ouiii ! >________< Excuse, le matin. :-° 1/2 alors. ^^ (\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x})}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}%20=%20\lim_{x\to%20+oo}\frac{x+\sqrt{x+\sqrt{x}}-x}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}=\lim_{x\to%20+oo}\frac{\sqrt{x}\sqrt{1+\frac{1}{\sqrt{x}}}}{\sqrt{x}(\sqrt{1+\sqrt{\frac{1}{x^2}+\frac{1}{x\sqrt{x}}}}+1)}=\frac{1}{2}) | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 10:39 Dim 21 Mar 2010, 10:39 | |
| Rien à dire. Poste-en une autre, toi qui est matinal  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 10:47 Dim 21 Mar 2010, 10:47 | |
| Voilà : tan(\frac{\Pi%20}{2x}a)) | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 11:41 Dim 21 Mar 2010, 11:41 | |
| bonjour on a une limite pareille dans notre DM mais c po la meme!! en fait j'ai utlisié 2 méthodes: la 1ere consiste sur la regle de l'hospital et qui donne vraiment comme limite 2a/pi or jé cherché une autre méthode jé trouvé ceci \tan&space;(\frac{\pi&space;a}{2x})=\frac{(x-a)sin(\frac{\pi&space;a}{2x})}{cos(\frac{\pi&space;a}{2x})}) on donne f(x)=cos(pi.x/2a) }{x-a}=f'(a)=\frac{\pi&space;}{2a}) conclure ke la limte est bien 2a/pi
Dernière édition par houssam110 le Dim 21 Mar 2010, 14:37, édité 2 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 12:51 Dim 21 Mar 2010, 12:51 | |
| Ou bien : Pose h=x-a x --> a <=> h --> 0 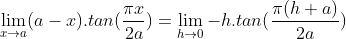 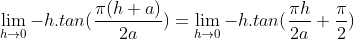 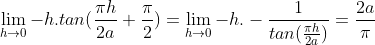 Conclusion : 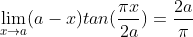 | |
|
  | |
houssam110
Expert sup

 Nombre de messages : 860 Nombre de messages : 860
Age : 31
Localisation : {Casa} U {Sefrou}
Date d'inscription : 19/04/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 14:46 Dim 21 Mar 2010, 14:46 | |
| - Sylphaen a écrit:
- Ou bien :
Pose h=x-a
x --> a <=> h --> 0
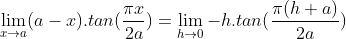
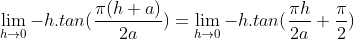
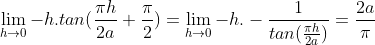
Conclusion :
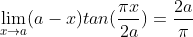 c'est po ckyé demandé sylphaen ya tan(a.pi/2x) et je pense po ke sa peu etre traité de telle maniere vu ke tu ora po comme sa le h ki tend vers 0 ... A+ | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  Dim 21 Mar 2010, 16:43 Dim 21 Mar 2010, 16:43 | |
| Tiens, je me demande si la généralisation suivante est correcte : \in%20IR%20/%20\lim_{x\to%200}\frac{1-Cos(a_{1}x)Cos(a_{2}x)Cos(a_{3}x)...Cos(a_{n}x)}{x^2}=%20\frac{\sum_{i=1}^{n}a_{i}^2}{2}) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: UN SUJET: Limites compliqués Sujet: Re: UN SUJET: Limites compliqués  | |
| |
|
  | |
| | UN SUJET: Limites compliqués |  |
|
