| | Marathon des équations fonctionnelles |  |
|
+360000 Misterayyoub kaj mima rimele expert_run az360 symizter abdelbaki.attioui Mehdi.O Sporovitch darkpseudo yasserito mizmaz King ali-mes L'enfant xyzakaria tarask nononabil nmo Othmaann Le criminelle kholoud-tetouanie MohE samia08 elhor_abdelali Othman24 majdouline imanos Bison_Fûté joystar1 oussama1305 Sylphaen pco M.Marjani Dijkschneier 40 participants |
|
| Auteur | Message |
|---|
L'enfant
Habitué
 Nombre de messages : 15 Nombre de messages : 15
Age : 31
Date d'inscription : 11/08/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 20 Déc 2010, 20:00 Lun 20 Déc 2010, 20:00 | |
| Il suffi de prendre y = 0 on a f(x) = f(x) +f(0)x donc f(0)x = 0 .. donc f(0) = 0 ou x = 0 .. mais puisque X et un variable dans R on a f(0) = 0 enfin .. je suppose et c'est moins compliqué ^^" | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 20 Déc 2010, 20:45 Lun 20 Déc 2010, 20:45 | |
| Cela prouve que f(0)=0 mais pas que f(x)=0 <=> x=0  | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 14 Jan 2011, 16:50 Ven 14 Jan 2011, 16:50 | |
| En attendant une solution complète de la part de xyzakaria au problème 40 je propose le 41 Problème 41Trouver toutes les fonctions f de Q+ vers Q+ vérifiant: +f(y)+2xyf(xy)=\frac{f(xy)}{f(x+y)}) - Spoiler:
P.S:l'une des plus difficiles équations fonctionnelles que j'ai jamais vues.
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 14 Jan 2011, 20:35 Ven 14 Jan 2011, 20:35 | |
| Q+ est privé de 0 ? Si ce n'est pas le cas :
Solution au problème 41 :
Pour x=y=0, il vient f(0)=1/2.
Pour y=0, il vient f(x) + 1/2 = 1/(2f(x))
<=> 2f(x)² + f(x) - 1 = 0
<=> f(x)=-1 ou f(x)=1/2
Ce qui permet de conclure que f(x)=1/2 pour tout x de Q+ puisque -1 n'est pas dans Im(f).
Mais inversement, cette fonction ne vérifie pas l'énoncé.
Synthèse :
L'EF n'admet aucune solution. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 14 Jan 2011, 20:43 Ven 14 Jan 2011, 20:43 | |
| Solution au problème 41 : Je suppose que Q+ ne contient pas 0 . On pose g(x)=1/ f(x) alors on a : 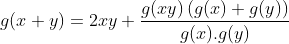 (*) Pour x=y=1 on a g(2)=4 et pour x=y=2 on trouve g(4)=16 . On pose g(1)=k et y=1 , alors on a : 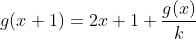 et : 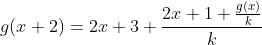 On fixe x=2 pour avoir : 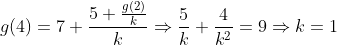 Donc : 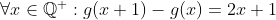 On effectue une récurrence simple pour avoir : \left (\forall x\in \mathbb{Q}^{+} \right ):g(x+n)-g(x)=2xn+n^2) (**) On pose x=p/q et y=q ( p,q des entiers >0 ) De la relation (*) on a : 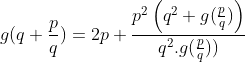 Et de la relation (**) on a : 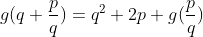 (*)+(**) => g(p/q)=p²/q² ( car g(p/q) > 0) ... Et le résultat en découle .. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 14 Jan 2011, 22:13 Ven 14 Jan 2011, 22:13 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 24 Jan 2011, 19:57 Lun 24 Jan 2011, 19:57 | |
| Problème 42 : (**** : quatre étoiles) : Trouver toutes les fonctions f : IR+ -> IR+ continues telles que : 1) f(f(x)) = x 2) %20=%20\frac{f(x)}{f(x)+1}) | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mar 25 Jan 2011, 12:32 Mar 25 Jan 2011, 12:32 | |
| - Dijkschneier a écrit:
- Problème 42 : (**** : quatre étoiles) :
Trouver toutes les fonctions f : IR+ -> IR+ continues telles que :
1) f(f(x)) = x
2) %20=%20\frac{f(x)}{f(x)+1}) Bonjour à tous. Evidemment, de pense que R+ est "à l'anglosaxonne", c'est dire sans 0. Sinon il n'y a pas de solution. de 1) on déduit que f est bijective et donc, comme bijection continue, monotone de 2) on déduit que f(x+1)<1 et donc que f(x)<1 pour tout x>1 et donc f est décroissante Donc, comme bijection continue décroissante, lim_{x->0}f(x)=+infini et, en appliquant celà à 2) on obtient f(1)=1 Soit alors A l'ensemble des réels positifs x tels que f(x)=1/x. A est non vide puisque 1 est dans A de 1) on déduit que si x est dans A, 1/x est dans A de 2) on déduit que si x est dans A, x+1 est dans A Il est alors aisé de montrer par récurrence que toute fraction continue de longueur finie est dans A Donc Q^+ est dans A Donc R^+ est dans A (continuité) Donc f(x)=1/x pour tour x>0 qui est bien une solution | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mar 25 Jan 2011, 12:51 Mar 25 Jan 2011, 12:51 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 26 Jan 2011, 19:28 Mer 26 Jan 2011, 19:28 | |
| Problème 43:Trouver toutes les fonctions définis sur IR+ telles que: 1)- \in%20\mathbb{R}^2_{+})f(xf(y))f(y)=f(x+y)) . 2)- ) f(z)=0 3)- 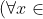 [0;2[ f(x)\neq%200)
Dernière édition par ali-mes le Mer 26 Jan 2011, 19:35, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 26 Jan 2011, 19:31 Mer 26 Jan 2011, 19:31 | |
| f(z) = 0 ?
Tu entends par là : il existe z tel que f(z)=0 ? | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 27 Jan 2011, 16:53 Jeu 27 Jan 2011, 16:53 | |
| - ali-mes a écrit:
- Problème 43:
Trouver toutes les fonctions définis sur IR+ telles que:
1)- \in%20\mathbb{R}^2_{+})f(xf(y))f(y)=f(x+y)) . .
2)-) f(z)=0 f(z)=0
3)- 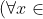 [0;2[ [0;2[ f(x)\neq%200) J'ai déjà présenté ma solution là-bas: https://mathsmaroc.jeun.fr/t17043-defi. Et j'attends encore une confirmation. | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 29 Jan 2011, 11:19 Sam 29 Jan 2011, 11:19 | |
| - ali-mes a écrit:
- Problème 43:
Trouver toutes les fonctions définis sur IR+ telles que:
1)- \in%20\mathbb{R}^2_{+})f(xf(y))f(y)=f(x+y)) . .
2)-) f(z)=0 f(z)=0
3)- 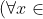 [0;2[ [0;2[ f(x)\neq%200) Bonjour, Désolé, nmo, je n'ai pas regardé votre démonstration, et je n'arrive pas à la même conclusion que vous. Notons bien sur que f(x)>=0 pour tout x (sinon 1 n'est pas toujours définie) Soit A={x tels que f(x)=0} et a=Inf(A)>=2 En choisissant y dans A dans la première équation, on a f(x+y)=0 pour tout x>=0 et donc f(x)=0 pour tout x>=y Donc f(x)=0 pour tout x>a et f(x) différent de 0 pour tout x<a Soit alors y<a Si f(y)>a/(a-y), soit alors x tel que a-y>x>a/f(y) : xf(y)>a et donc f(xf(y))=0 et donc f(x+y)=0 mais on a x+y<a, et donc contradiction Si f(y)<a/(a-y), soit alors x tel que a-y<x<a/f(y) : xf(y)<a et donc f(xf(y)) et f(y) sont non nuls et donc f(x+y) est non nul mais on a x+y>a, et donc contradiction Donc f(y)=a/(a-y) pour tout y<a Soit alors y<a et x=a-y. L'équation 1 donne f(a)a/x=f(a) et donc f(a)=0 D'où la réponse, dont il est facile de vérifier que c'est effectivement une solution : Soit a>=2 quelconque : f(x)=a/(a-x) pour tout x<a f(x)=0 pour tout x>=a | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Dim 30 Jan 2011, 16:49 Dim 30 Jan 2011, 16:49 | |
| - pco a écrit:
- Désolé, nmo, je n'ai pas regardé votre démonstration, et je n'arrive pas à la même conclusion que vous.
Certes, en effet ma démonstration est érronée et je comprends ma faute, je vais supprimer ma solution immédiatement. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 02 Fév 2011, 17:11 Mer 02 Fév 2011, 17:11 | |
| Pour mettre au point le problème, je n'ai pas résolu celui-là que tu viens de résoudre pco, mais j'ai résolu celui-ci: https://mathsmaroc.jeun.fr/t17087-eq-fonc. La différence réside dans la deuxième condition. Au plaisir! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 02 Fév 2011, 17:37 Mer 02 Fév 2011, 17:37 | |
| Je propose un nouvel problème, à ta place pco: Problème 44:Trouvez toutes les fonctions f et g, tel que \in\mathbb{R}):f\circ g(x)=2x^2+1\text{ et }g\circ f(x)=(2x+1)^2) . Bonne chance.P.S: Je ne dispose d'aucune solution à ce problème. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Dim 20 Fév 2011, 18:36 Dim 20 Fév 2011, 18:36 | |
| Problème 45 : (*** : trois étoiles)
Trouver toutes les fonctions de IR vers IR qui vérifient l'EF : f(xf(x+y)) = f(yf(x))+x².
Dernière édition par Dijkschneier le Mer 06 Avr 2011, 14:12, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 06 Avr 2011, 13:33 Mer 06 Avr 2011, 13:33 | |
| J'ai édité le problème courant. | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 06 Avr 2011, 15:13 Mer 06 Avr 2011, 15:13 | |
| Salut Nizar  J'espère que tu es bien arrivé  , tu me manques déjà mec  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 06 Avr 2011, 15:26 Mer 06 Avr 2011, 15:26 | |
| | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 06 Avr 2011, 15:28 Mer 06 Avr 2011, 15:28 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 | |
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 06 Avr 2011, 21:26 Mer 06 Avr 2011, 21:26 | |
| Salut King  Et  pour la solution de M.Marjani... Appelez Oussama Elmir... | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 06 Avr 2011, 22:04 Mer 06 Avr 2011, 22:04 | |
| - Dijkschneier a écrit:
- Salut King

Et  pour la solution de M.Marjani... pour la solution de M.Marjani...
Appelez Oussama Elmir... MDRRR : Marjani, tu as utilisé combien de lemmes dans ta solution, ces lemmes sont les tiennes? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  | |
| |
|
  | |
| | Marathon des équations fonctionnelles |  |
|
