| | Marathon des équations fonctionnelles |  |
|
+360000 Misterayyoub kaj mima rimele expert_run az360 symizter abdelbaki.attioui Mehdi.O Sporovitch darkpseudo yasserito mizmaz King ali-mes L'enfant xyzakaria tarask nononabil nmo Othmaann Le criminelle kholoud-tetouanie MohE samia08 elhor_abdelali Othman24 majdouline imanos Bison_Fûté joystar1 oussama1305 Sylphaen pco M.Marjani Dijkschneier 40 participants |
|
| Auteur | Message |
|---|
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 23 Sep 2010, 09:40 Jeu 23 Sep 2010, 09:40 | |
| - nononabil a écrit:
- Je suis nouveau sur cet espace permettez moi de partager cet exo interessant
Probleme 34 :
Determinez toutes les applications definies de N dans N tel que : f(f(n))<f(n+1) Bon, puisque personne ne donne de solution  : - Spoiler:
On va démontrer par récurrence l'assertion A(n) :
f(k)=k pour tout k<n et f(k)>f(n)>= n pour tout k>n
Démarrage de la récurrence : démontrons A(0)
f(k)=k pour tout k<0 ne pose pas de problèmes
Soit maintenant m=min(f(x), x>=0) et soit a>=0 tel que f(a)=m
si a>0, alors m=f(a)>f(f(a-1)) ce qui est impossible, par définition de m. Donc a=0 et m=f(0) et
f(k)>f(0)>=0 pour tout k>0
et donc A(0) est vrai
Etape de récurrence: Supposons A(n) vrai pour un certain n>=0
Soit m=min(f(x), x>= n+1) et soit a>=n+1 tel que f(a)=m
a-1>=n>=0 et donc m=f(a)>f(f(a-1)) ce qui implique f(a-1)<=n (définition de m)
Si a-1>n, l'assertion A(n) implique f(a-1)>n, en contradiction avec la ligne précédente. Donc a-1=n et a=n+1 et donc f(k)>f(a) pour tout k>n+1
f(a-1)<=n devient f(n)<=n et comme A(n) nous dit f(n)>=n, on obtient f(n)=n.
A(n) nous dit alors f(n+1)>f(n) et donc f(n+1)>=n+1
Et nous avons :
f(k)=k pour tout k<n (A(n)) et f(n)=n et donc f(k)=k pour tout k<n+1
f(k)>f(n+1)>=n+1 pour tout k>n+1
Et donc A(n+1)
Et donc A(n) vrai pour tout n et donc la seule solution f(n)=n, qui se trouve effectivement être une solution.
Et libre à chacun de poser un autre problème | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 23 Sep 2010, 12:13 Jeu 23 Sep 2010, 12:13 | |
| Solution au problème 34 :Source : https://mathsmaroc.jeun.fr/equations-fonctionnelles-f10/equation-fonctionelle-t16342.htm- Spoiler:
Soit f une fonction éventuelle vérifiant les conditions de l'énoncé. Pour tous entier naturel n, f(n+1)>f(f(n)), cela implique que pour tout entier non nul n, f(n)>=1. - Supposons dans un premier temps que f(0)>=1. Alors maintenant, pour tout entier naturel tout court, f(n)>=1. Nous allons montrer qu'une telle fonction f ne peut exister. Soit n de IN. Puisque f(n)>=1, alors des nombres tels que f(f(n)-1) sont des entiers naturels. Selon l'hypothèse, f(n+1)>=f(f(n))+1. Par récurrence, on montre alors que pour tout entier k plus grand ou égal à 1 :  Pour k=f(n+1), ce qui est possible car f(n+1)>=1, la contradiction est évidente. De fait, f n'existe pas dans ce cas. - Voyons maintenant ce qui se passe lorsque f(0)=0. On remarque pour de petites valeurs que f(1)>=f(f(0))+1=1, f(2)>=f(f(1))+1>=f(f(f(1)-1)) + 2>=2, etc., c'est-à-dire, f(n)>=n. Montrons, quant à nous, par récurrence forte sur n, que  . Initialisation : pour n=0, f(0)=0. Tout entier naturel est supérieur ou égal à 0 (k>=0). De plus, f est à valeurs dans IN, donc f(k)>=0. Hérédité : supposons qu'aux rangs 1<=i<=n,  . Pour simplifier et bien comprendre, supposons aussi que n>=2. Montrons que  . Alors :  Ouf ! Fin de la récurrence. Nous avons montré que  . Pour k=n en particulier, il vient f(n)>=n pour tout entier naturel n. L'hypothèse f(n+1)>f(f(n)) implique alors que f(n+1)>f(n), c'est-à-dire que f est strictement croissante. Par conséquent, l'hypothèse f(n+1)>f(f(n)) implique que n+1>f(n). Ainsi, n+1>f(n)>=n, donc f(n)=n. Inversement, l'identité sur IN vérifie les conditions de l'énoncé.
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 25 Sep 2010, 15:37 Sam 25 Sep 2010, 15:37 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 01 Oct 2010, 12:50 Ven 01 Oct 2010, 12:50 | |
| Problème 35:Trouvez toutes les fonction définies de IR vers IR qui satisfont la relation suivantre: \in\mathbb{R}^2)(\forall n\in\mathbb{N}^*):f(x^n)f(y^n)=f(x^ny^n)+f(x^n)+f(y^n)-2) . Bonne chance. | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 02 Oct 2010, 14:25 Sam 02 Oct 2010, 14:25 | |
| - nmo a écrit:
- Problème 35:
Trouvez toutes les fonction définies de IR vers IR qui satisfont la relation suivantre:
\in\mathbb{R}^2)(\forall n\in\mathbb{N}^*):f(x^n)f(y^n)=f(x^ny^n)+f(x^n)+f(y^n)-2) . .
Bonne chance. Bonjour, Voici ma solution : - Spoiler:
Tout d'abord, remarquons que n n'est là que pour compliquer inutilement le problème. Si l'équation est vraie pour n=1, elle est vraie pour tout n. Ne conservons donc que n=1
Posons ensuite f(x)=g(x)+1 et on trouve P(x,y) : g(xy)=g(x)g(y) qui est vraiment très classique :
Si il existe u non nul tel que g(u)=0, alors P(x/u,u) implique g(x)=0 pour tout x
Si g(0) est non nul, alors P(x,0) implique g(x)=1 pour tout x
Il reste à étudier le cas ou g(0)=0 et g(x) non nul pour tout x non nul
P(x,x) montre que g(x)>0 pour tout x non nul
P(1,1) donne g(1)=1
P(-1,-1) donne g(-1)=1 ou g(-1) = -1
La connaissance d'une solution t(x) pour x>0 nous donne donc deux solutions pour x<0 : t(-x) ou -t(-x) et donc :
t(|x|) et signe(x)t(|x|)
Posons, pour x>0, g(x)=e^h(ln(x)) avec h de R dans R et l'équation devient h(x+y)=h(x)+h(y) et donc h(x) est n'importe quelle solution de l'équation de Cauchy.
Ce qui nous donne finalement comme solutions :
f(x)=1 pour tout x
f(x)=2 pour tout x
f(0)=1 et f(x)=1+e^h(ln(|x|)) pour tout x non nul avec h(x) solution quelconque de l'équation de Cauchy
f(0)=1 et f(x)=1+signe(x)e^h(ln(|x|)) pour tout x non nul avec h(x) solution quelconque de l'équation de Cauchy
Qui sont bien toutes quatre des solutions.
Et libre à tous de donner un autre problème | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 23 Oct 2010, 14:27 Sam 23 Oct 2010, 14:27 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 23 Oct 2010, 18:58 Sam 23 Oct 2010, 18:58 | |
| - Dijkschneier a écrit:
- Quoi d'autre ?
Problème 36:Déterminez toutes les fonctions définies de  vers  et qui satisfont les deux relations suivantes: f(0)=1 et =\frac{2f(n)}{3+\sqrt{f(n)}}) pour tout entier n. Bonne chance. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 23 Oct 2010, 19:06 Sam 23 Oct 2010, 19:06 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 23 Oct 2010, 21:40 Sam 23 Oct 2010, 21:40 | |
| - nmo a écrit:
Problème 36:
Déterminez toutes les fonctions définies de  vers vers  et qui satisfont les deux relations suivantes: f(0)=1 et et qui satisfont les deux relations suivantes: f(0)=1 et =\frac{2f(n)}{3+\sqrt{f(n)}}) pour tout entier n. pour tout entier n.
Bonne chance. Merci pour l'exercice, mais honnêtement... L'exercice n'est pas intéressant car cette fonction est déterminée complètement et directement par les conditions fournies par l'énoncé : f est initialisée et, à partir de la valeur de la fonction au rang n, on calcule la valeur de la fonction au rang n+1, et ainsi, f est complètement définie. Il ne reste donc plus qu'à "deviner" la forme de la fonction, si l'on veut, et montrer qu'en effet cette fonction vérifie les conditions, puisqu'elle est unique. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 23 Oct 2010, 23:03 Sam 23 Oct 2010, 23:03 | |
| J'ai passé toute une heure à y réfléchir , j'ai songé aux suites d'abord , plus précisément le polynôme caractéristique , c'est une bonne idée, mais qui n'a malheureusement pas marché ici puisqu'il semble être impossible de trouver la relation récurrente U_(n+2)=aU_(n+1)+bU_n ! Merci pour l'exercice nmo  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 27 Oct 2010, 19:13 Mer 27 Oct 2010, 19:13 | |
| Problème 37:Déterminez toutes les fonctions définies de [ 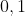 ] vers [ 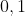 ] et qui satisfont la relation suivante: -f(y)|\ge|x-y|) pour tout les réels x et y qui appartiennent à [ 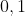 ]. Bonne chance. | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 28 Oct 2010, 07:08 Jeu 28 Oct 2010, 07:08 | |
| - nmo a écrit:
- Problème 37:
Déterminez toutes les fonctions définies de [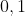 ] vers [ ] vers [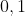 ] et qui satisfont la relation suivante: ] et qui satisfont la relation suivante:
-f(y)|\ge|x-y|) pour tout les réels x et y qui appartiennent à [ pour tout les réels x et y qui appartiennent à [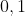 ]. ].
Bonne chance. Bonjour nmo, Pouvez-vous nous donner votre solution au problème 36, maintenant que vous proposez le 37 ? Merci beaucoup. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 28 Oct 2010, 16:45 Jeu 28 Oct 2010, 16:45 | |
| | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 28 Oct 2010, 18:35 Jeu 28 Oct 2010, 18:35 | |
| - nmo a écrit:
- Problème 37:
Déterminez toutes les fonctions définies de [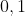 ] vers [ ] vers [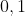 ] et qui satisfont la relation suivante: ] et qui satisfont la relation suivante:
-f(y)|\ge|x-y|) pour tout les réels x et y qui appartiennent à [ pour tout les réels x et y qui appartiennent à [ ]. ]. Ma solution : - Spoiler:
Soit P(x,y) l'assertion |f(x)-f(y)|>=|x-y|
Si f(x) est solution, alors 1-f(x) est solution aussi. Considérons donc sans perte de généralité que f(1)>=f(0)
P(1,0) ==> f(1)-f(0)>=1 et donc f(1)=1 et f(0)=0
P(x,0) ==> f(x)>=x
P(1,x) ==> 1-f(x)>=1-x ==> f(x) <= x
Donc f(x)=x
D'où les deux solutions :
f(x)=x
f(x)=1-x
Et que chacun se sente libre d'en proposer une nouvelle à ma place | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 29 Oct 2010, 19:02 Ven 29 Oct 2010, 19:02 | |
| Bravo pco. Toujours aux aguets du moindre trafic d'équations fonctionnelles sur ce forum, décidément. | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 29 Oct 2010, 19:43 Ven 29 Oct 2010, 19:43 | |
| - Dijkschneier a écrit:
- Bravo pco. Toujours aux aguets du moindre trafic d'équations fonctionnelles sur ce forum, décidément.
Oui, j'adooooore les ef  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 11 Nov 2010, 18:36 Jeu 11 Nov 2010, 18:36 | |
| Problème 38:
Déterminez toutes les fonctions définies de IR vers IR et qui satisfont la relation suivante: f(x-f(y))=f(f(y))+xf(y)+f(x)-1 pour chaque couple des réels (x,y).
Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 11 Nov 2010, 19:47 Jeu 11 Nov 2010, 19:47 | |
| Solution au problème 38 :- Spoiler:
1- En posant x=f(y), on montre que )%20=%20\frac{f(0)+1}{2}%20-%20\frac{f(y)^2}{2}) 2- En faisant x->f(x) et en utilisant 1-, on montre que -f(y))=%20f(0)%20-%20\frac{(f(x)%20-%20f(y))^2}{2}) 3- On montre que f(0) est nécessairement non nul. 4- En posant y=0 et ^2%20+%201%20-%20f(0)}{2}}{f(0)}) , on montre que ^2%20+%201%20-%20f(0)}{2}}{f(0)}%20-%20f(0))%20-%20f(\frac{y+\frac{f(0)^2%20+%201%20-%20f(0)}{2}}{f(0)})%20=%20y) 5- En posant dans 2- ^2%20+%201%20-%20f(0)}{2}}{f(0)}%20-%20f(0)) et ^2%20+%201%20-%20f(0)}{2}}{f(0)}) , on montre que f(a)=f(0)-a²/2. Inversement, toute fonction de la forme f(x)=a-x²/2 où a est un réel non nul est une solution à l'EF ( à vérifier)
Sauf erreur. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Dim 14 Nov 2010, 10:31 Dim 14 Nov 2010, 10:31 | |
| Problème 39 :
Trouver toutes les fonctions définies sur IN et à valeurs dans IN telles que : f(n) + f(f(n)) + f(f(f(n))) = 3n | |
|
  | |
xyzakaria
Expert grade2
 Nombre de messages : 374 Nombre de messages : 374
Age : 31
Date d'inscription : 12/12/2008
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Nov 2010, 16:57 Ven 19 Nov 2010, 16:57 | |
| bonjour,.... Solution au problème 39 :- Spoiler:
soit f une fonction eventuelle
il est facile de remarquer que f est injective en effet si f(m)=f(n) alors on a : fof(n)=fof(m) et fofof(n)=fofof(m) d'ou le résultat...
n=0------>f(0)+fof(0)+fofof(0)=0==>f(0)=0
soit m£IN on suppose que pour tt n=<m on a : f(n)=n...(donc on a aussi fof(n)=n et fofof(n)=n)
prouvons par principe de reccurence que f(m+1)=m+1...comme f est injective alors on aurra forcemment f(m+1)>=m+1 et encore fof(m+1)>=m+1 et fofof(m+1)>=m+1...Or; leurs somme est égale a 3m+3 d'après l'équation initial...d'ou le resultat....
réciproquement la fonction n--->n vérifie les conditions...
Sauf erreur....
Dernière édition par xyzakaria le Sam 20 Nov 2010, 09:13, édité 2 fois | |
|
  | |
xyzakaria
Expert grade2
 Nombre de messages : 374 Nombre de messages : 374
Age : 31
Date d'inscription : 12/12/2008
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Nov 2010, 19:37 Ven 19 Nov 2010, 19:37 | |
| j'attends une confirmation pour que je propose un exo  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Nov 2010, 20:01 Ven 19 Nov 2010, 20:01 | |
| | |
|
  | |
xyzakaria
Expert grade2
 Nombre de messages : 374 Nombre de messages : 374
Age : 31
Date d'inscription : 12/12/2008
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Nov 2010, 20:20 Ven 19 Nov 2010, 20:20 | |
| problème 40
f:IR-->IR et vérifie : pour tout (x,y)£IR² / f(x+yf(x))=f(x)+xf(y)
je suis dsl je viens de lire les régles...mnt ca va :p
Dernière édition par xyzakaria le Sam 20 Nov 2010, 09:15, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Nov 2010, 21:43 Ven 19 Nov 2010, 21:43 | |
| Numérote tes problèmes, sinon on n'y répond pas.
Numérote ta précédente solution aussi.
Lire les règles du marathon avant toute intervention. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 15 Déc 2010, 15:54 Mer 15 Déc 2010, 15:54 | |
| Voici un début de preuve au problème 40 :
Soit f une solution à l'EF.
Pour x=0, il vient f(yf(0))=f(0).
- Si f(0) est non nul, alors on peut diviser par f(0), et la transformation y |-> y/f(0) nous permet justement de voir que f(y)=f(0), pour tout réel y. Cela veut dire que f est constante, et parmi les fonctions constantes, la fonction nulle est la seule solution à l'EF.
Inversement, la fonction nulle est une solution à l'EF.
- Supposons désormais que f(0)=0 et f non identiquement nulle.
Soit c un réel tel que f(c)=0 et d un réel tel que f(d) est non nul.
Pour x=c et y=d, il vient 0=cf(d), donc c=0.
On a ainsi établi que : f(x)=0 <=> x=0.
Et voici des résultats en vrac à propos du problème 40 :
- Si l'ensemble des points fixes de f n'est pas IR tout entier, alors son complémentaire est infini.
- f(x)=-1 <=> x=-1
Je serais intéressé par une solution complète au problème 40. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  | |
| |
|
  | |
| | Marathon des équations fonctionnelles |  |
|
