| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 15:56 Jeu 18 Aoû 2011, 15:56 | |
| Problème 91:Soient x;y;z>=0 Prouver que: ^2\geq&space;9(x^2+yz)(y^2+zx)(z^2+xy)) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 16:16 Jeu 18 Aoû 2011, 16:16 | |
| Solution au problème 91:- Spoiler:
Nous avons : \leq&space;9(\frac{x^2+y^2+z^2+xy+xz+yz}{3})^{3}\leq&space;\frac{8}{3}(x^2+y^2+z^2)^3) . Ainsi il suffit de prouver que : ^2\geq&space;\frac{1}{3}(\sum&space;x^{2})^3) . Mais par C.S:, nous avons : ^2\geq&space;\frac{(\sum&space;x^2)^4}{(\sum&space;x)^2}\geq&space;\frac{1}{3}(\sum&space;x^{2})^{3}\Leftrightarrow&space;\sum&space;x^{2}\geq&space;\frac{1}{3}(\sum&space;x)^{2}) Ce qui est clairement vrai. Sauf erreur.. 
Problème 92:Soit a,b,c,d >0 t.q: a+b+c+d =1. Prouver que : 
Dernière édition par Mehdi.O le Jeu 18 Aoû 2011, 16:24, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 16:22 Jeu 18 Aoû 2011, 16:22 | |
| - Mehdi.O a écrit:
- Solution au problème 91:
- Spoiler:
Nous avons : \leq&space;9(\frac{x^2+y^2+z^2+xy+xz+yz}{3})^{3}\leq&space;\frac{8}{3}(x^2+y^2+z^2)^3) .
C'est 9 pas 8 . | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 16:23 Jeu 18 Aoû 2011, 16:23 | |
| - az360 a écrit:
- Mehdi.O a écrit:
- Solution au problème 91:
- Spoiler:
Nous avons : \leq&space;9(\frac{x^2+y^2+z^2+xy+xz+yz}{3})^{3}\leq&space;\frac{8}{3}(x^2+y^2+z^2)^3) .
C'est 9 pas 8 . Oui juste uen faute de frappe  . Merci pour ta vigilence. | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 17:54 Jeu 18 Aoû 2011, 17:54 | |
|
Dernière édition par kaj mima le Jeu 18 Aoû 2011, 19:47, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 18:10 Jeu 18 Aoû 2011, 18:10 | |
|
Dernière édition par expert_run le Jeu 18 Aoû 2011, 22:30, édité 1 fois | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 18:16 Jeu 18 Aoû 2011, 18:16 | |
| Re...Désolée pour le retard. Alors en voici un nouveau: Problème 93:a,b et c sont les longueurs des côtés d'un triangle, montrer que:  tel que S est la surface du triangle. | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 18:51 Jeu 18 Aoû 2011, 18:51 | |
| problème 93
on sait que selon héron S=rac(p(p-a)(p-b)(p-c))
=rac((a+b+c)(b+c-a)(a+c-b)(a+b-c)/16)
et d'après le problème 90 déjà résolu : on a obtenu:
(a+b+c)(b+c-a)(a+c-b)(a+b-c)=<(a²+b²+c²)²/3
donc :: S=<rac(a²+b²+c²)²/(16*3))
donc 4sqrt3=<a²+b²+c²
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 18:55 Jeu 18 Aoû 2011, 18:55 | |
| - kaj mima a écrit:
- Solution au problème 92:
- Spoiler:
On a a,b,c,d >0 et a+b+c+d=1 alors: a,b,c,d 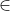 ]0,1[ La fonction =\frac{1+\sqrt{x}}{1-x}) est convexe sur l'intervalle [0,1[ Alors, selon Jensen: ) Par suite: =&space;4*2&space;=8) C.Q.F.D
NON, f n'est pas convexe sur ]0;1[: http://www.wolframalpha.com/input/?i=%28\frac{1%2B\sqrt{x}}{1-x}%29%27%27%3E0&asynchronous=false&equal=Submit | |
|
  | |
xyzakaria
Expert grade2
 Nombre de messages : 374 Nombre de messages : 374
Age : 31
Date d'inscription : 12/12/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 18:59 Jeu 18 Aoû 2011, 18:59 | |
| si elle est convexe sur l intervalle [0,1[.. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 19:00 Jeu 18 Aoû 2011, 19:00 | |
| - xyzakaria a écrit:
- si elle est convexe sur l intervalle [0,1[..
hmm, elle est pas convexe sur ]0;1/9[ | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 19:05 Jeu 18 Aoû 2011, 19:05 | |
| libre à vous de poster un nouveau problème. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 19:11 Jeu 18 Aoû 2011, 19:11 | |
| - manazerty a écrit:
- libre à vous de poster un nouveau problème.
Le problème 92 est encore en jeu. | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 19:12 Jeu 18 Aoû 2011, 19:12 | |
|
Dernière édition par kaj mima le Jeu 18 Aoû 2011, 19:47, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 18 Aoû 2011, 19:45 Jeu 18 Aoû 2011, 19:45 | |
| Qu'est-ce-qui se passe ici :O ... @kaj mima: Ta solution est erronée, la fonction n'est pas convexe, et Jensen est inapplicable dans cette inégalité, je n'aurais quand même pas posté une inégalité aussi triviale qui sera juste une application directe. Je te prie de supprimer ta solution, et le problème que tu as posté. Merci pour ta compréhension  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 00:18 Ven 19 Aoû 2011, 00:18 | |
| Ma réponse pour problème 92:Soient a,b,c,d>0 tel que a+b+c+d=1. On a: (1+\sqrt{a})}\geq%208)  Et on a d'après l'inégalité de CS: %20\right%20)%20\left%20(\sum%20\frac{1}{1-\sqrt{a}}%20\right%20)\geq%2016) . }) . Donc pour montrer l'inégalité proposée, il suffit de montrer que: }\geq%208\Leftrightarrow%20\frac{2}{\sum%20(1-\sqrt{a})}\geq%201\Leftrightarrow%20\sum%20(1-\sqrt{a})\leq%202) .  . Maintenant, vu la concavité de la fonction: 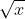 sur IR+, on a:  . D'où le résultat voulut. J'attends une confirmation pour poster un nouveau problème. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 00:21 Ven 19 Aoû 2011, 00:21 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 00:26 Ven 19 Aoû 2011, 00:26 | |
| | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 00:28 Ven 19 Aoû 2011, 00:28 | |
| Bonsoir tout le monde .  tels que a,b,c,d > 0 et a+b+c+d=1 tout d'abord montrons la lemme suivante :  On a  On fait la meme chose pour b,c,d , en sommant .. CQFD  Que quelqu'un se sente libre pour poster une nouvelle inégalité !
Dernière édition par Misterayyoub le Ven 19 Aoû 2011, 00:30, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 00:29 Ven 19 Aoû 2011, 00:29 | |
| | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 01:48 Ven 19 Aoû 2011, 01:48 | |
| je crois que la solution de misterayyoub est claire et juste, donc je poste un nouveau problème:
problème 94:
soient a,b,c des nombres réels et positifs, avec: abc=1
MQ:
1/(a3(b+c)) +1/(b3(c+a))+ 1/(c3(a+b)) >= 3/2 | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 02:08 Ven 19 Aoû 2011, 02:08 | |
| Bonsoir encore une fois . Nous devons demontrer l'inegalité suivante :  tel que abc=1 et a,b,c appartiennent a R+ faisons les substitions suivantes : a=1/x , b=1/y , c=1/z , ce qui donne xyz=1 , l'inegalité devienne :  Par CS , on a :  CQFD  | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 02:26 Ven 19 Aoû 2011, 02:26 | |
| C'est juste. Poste une autre  | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 02:33 Ven 19 Aoû 2011, 02:33 | |
| Je trouve pas pour l'instant , Vous pouvez posté une nouvelle inégalité . Au plaisir ..  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 19 Aoû 2011, 02:44 Ven 19 Aoû 2011, 02:44 | |
| Problème 95:Soient a;b;c € IR+ tel que abc=1 prouver que:  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
