Le marathon des inégalités:

Très connue en fait sous le nom de série de Riemann (ici cas de alpha=2) .

Steve 94 tu peux poster un nouveau problème; puisque moi j'en ai pas.

Voilà et merci expert_run

https://i.servimg.com/u/f42/16/62/75/03/codeco21.gif

Bonsoir,

En sommant , on obtient l'inégalité désirée .
Plutôt facile pour inégalité d'un Marathon ... non ?

tarask a écrit:

Bonsoir,

En sommant , on obtient l'inégalité désirée .
Plutôt facile pour inégalité d'un Marathon ... non ?

Oui surement on va utiliser ca. Alors je vais poster une solution complète.

steve 94 a écrit:

Voilà et merci expert_run
Problème 85:
https://i.servimg.com/u/f42/16/62/75/03/codeco21.gif

Solution 85
On a
Donc

Problème 86:

Soit une séquence d'entiers positifs distincts.
Prouver que pour tout entier positif n :

...........

steve 94 a écrit:

https://i.servimg.com/u/f42/16/62/75/03/codeco23.gif

Je crois .

Oh non c'est faux(je pense). Je te dis que c'est un exercice de l'imo et ça demande du travail.

Ouais merci ,j'essairai une autre méthode !

expert_run a écrit:

Problème 86:

Soit une séquence d'entiers positifs distincts.
Prouver que pour tout entier positif n :

Il suffit de remarquer que est une permutation de {1,2,...,n} puis d'utiliser l'inégalité du réordonnement.

expert_run a écrit:

Problème 86:

Soit une séquence d'entiers positifs distincts.
Prouver que pour tout entier positif n :

Solution pour le problème 86:

Spoiler:

Problème 87:

Soit a,b,c>0 et n € IN*
Prouver que :

Solution du problème 87:

Par symétrie des rôles, on suppose que: a>=b>=c ===> a^(n-1)>=b^(n-1)>=c^(n-1)
et 1/b+c >= 1/a+c >= 1/a+b ===> a/b+c >= b/a+c >= c/a+b

Selon Chebyshev:

Et selon Nesbitt:

Par conséquent:

C.Q.F.D

@Kaj mima : à vous de proposer .

Problème 88:

a,b,c des réels strrictement positifs.
Montrer que:

Ma réponse pour problème 88:

Soient a,b et c des réels strictement positives, on a:



.

D'après la lemme de Titu, on a:



Donc pour montrer l'inégalité proposée, il suffit de montrer que:







.

Ce qui est vrai, d'où le résultat voulut.

Problème 89:

Soient a, b et c des réels strictement positifs tel que ab+ac+bc=1.

Montrer que: .

geom a écrit:

tu peux poster une démonstration pour la lemme de Titu svp.

C'est juste une application de Cauchy-schwartz
on a :

D'où la conclusion.

Solution au problème 89:
L'inégo est équivalente à :

Mais nous avons :

Et :
Ainsi

Probleme 90 :
Soient a, b et c des réels strictement positifs .
Montrer que : .

Mehdi.O a écrit:

Solution au problème 89:
L'inégo est équivalente à :

Mais nous avons :

Et :
Ainsi

pourquoi??(d'après quel théorème au juste?!)

manazerty a écrit:

Mehdi.O a écrit:

Solution au problème 89:
L'inégo est équivalente à :

Mais nous avons :

Et :
Ainsi

pourquoi??(d'après quel théorème au juste?!)

C'est trivial, sans avoir recours à aucun théorème vu que c'est équivalent à : a²(b-c)²+b²(a-c)²+c²(a-b)²>=0

manazerty a écrit:

Mehdi.O a écrit:

Solution au problème 89:
L'inégo est équivalente à :

Mais nous avons :

Et :
Ainsi

pourquoi??(d'après quel théorème au juste?!)

tu peut poster ab = A et ac = B et bc = C pour retour a :
A² + B² + C² >= AB + BC+CA (ce qui clair)

ok merci.

az360 a écrit:

Probleme 90 :
Soient a, b et c des réels strictement positifs .
Montrer que : .

Solution pour le problème 90:
Par symétrie on suppose que :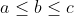

Donc b+c-a> =0 ; a+c-b>=0 et a+b-c est soit positif soit négatif.
Si a+b-c=<0 l'inégalité est trivial.
Si a+b-c>=0 :


Et selon C.S:

Donc