Le marathon des inégalités:

merci Mr radouane_BNE

je ne l'ai tellement pas fait attention. merci Mr younesmath2012 je vais essayer de trouver une solution maintenant

Par contre, celle-ci est résolue parfaitement par Lagrange, soit f(lambda,x,y)=3x^2+2y^3+lambda(x+y^2-x^2-y^3). on a alors:

f_x=6x+lambda(1-2x)=0
f_y=6y+lambda(2y-3y^2)=0
f_lambda=x+y^2-x^2-y^3=0

ce sytème admet pour solutions réelles (0,0,0),(1,0,6),(1,1,6),il reste juste de vérifier en calculant la matrice hessienne que (1,1,6) réalise le maximum global.

Je propose un nouveau problème:
Problème 138:
Soient , et trois nombres positifs non tous nuls.
Montrez que .
Bonne chance.

il faut d'abord completer la solution de l'exercice 137 !!!

la matrice hessienne est tout simple à calculer, après le calcul du determinant est tout simple (matrice d'ordre 3), appliquer le determinant aux trois points est tout simple....qu'est ce qui reste à compléter!

ok voici une simple solution (am-gm) :



remarque : on a seulement x reel et y >=0 .

nmo a écrit:

Je propose un nouveau problème:
Problème 138:
Soient , et trois nombres positifs non tous nuls.
Montrez que .
Bonne chance.

ta constante ne me plait pas cher nmo   ,quand est ce que le cas d'égalité  

alidos a écrit:

nmo a écrit:

Je propose un nouveau problème:
Problème 138:
Soient , et trois nombres positifs non tous nuls.
Montrez que .
Bonne chance.

ta constante ne me plait pas cher nmo    ,quand est ce que le cas d'égalité  

Le cas d'égalité est lorsque a=0, et b=c... Et les autres permutations.

Bon je pense que cette solution est fausse....l'homogénéisation a+b+c=1 permet d'écrire l'inégalité suivante:


la fonction est concave sur [0,1], par Jensen on obtient :


il suffit ainsi de démontrer que :


on applique encore une fois Jensen sur la fonction concave sur [0,1], ce qui donne :


or on a bien :


soit ma preuve est fausse, soit la constante à gauche n'est pas stricte.

radouane_BNE a écrit:

soit ma preuve est fausse, soit la constante à gauche n'est pas stricte.

Je pense que le fait d'homogéniser nuit au cas d'égalité qui est atteint lorsue l'une des variables est nulle et les deux autres égales.
L'inégalité figure dans un compte rendu d'un certain stage de l'équipe française, et dont les écrivains ont préféré en donner une solution très longue (deux pages et demie) en utilisant la technique des multiplicateurs de Lagrange...

La technique des multiplicateurs de Lagrange donne la plupart du temps un résultat.
Mais elle est aussi la plupart du temps moche, c'est pour ça que pour l'inégalité de l'autre jour j'ai préféré ne pas terminer la démarche vu qu'elle est assez compliquée et contient une montagne de calculs.

J'ai fait mon dernier post sans vérification de la solution proposée. Lorsque c'est fait, le passage suivant:

radouane_BNE a écrit:

on applique encore une fois Jensen sur la fonction concave sur [0,1], ce qui donne :

est faux, car la fonction citée est convexe...
D'ailleurs, l'inégalité arithmético-géométrique donne: , soit encore .
Une solution de ce problème se trouve dans la page 57 de ce livre: www.animath.fr/IMG/pdf/poly_final_sansphotos.pdf.
Au plaisir!

Je propose un nouveau problème dont je ne dispose pas de solution:
Problème 139:
Soient , et des nombres réels de l'intervalle ][ vérifiant .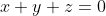
Montrez que: .
Bonne chance.