Le marathon des inégalités:

il faut d'abord resoudre le probleme 131.merci!!!

younesmath2012 a écrit:

Solution problème 131:
Par Chebyshev:
3(a^3+b^3+x^3+y^3)>=3 (a²+b²+x²+y²)=2(a²+b²+x²+y²)+(a²+b²+x²+y²)>= 2(a²+b²+x²+y²)+((a+b+x+y)²/4)=2(a²+b²+x²+y²)+4

Libre à chacun de poster.

pourquoi on a 3(a^3+b^3+x^3+y^3)>=3 (a²+b²+x²+y²)???????????
il faut la montrer

(a+b+c+d)(a^3+b^3+c^3+c^3) akbar mn (a²+b²+c²+d²)²
mais on a : a²+b²+c²+d² akbar mn 4 d'apres C.S donc
(a^3+b^3+c^3+c^3) akbar mn (a²+b²+c²+d²)*(a²+b²+c²+d²)/4 akbar mn a²+b²+c²+d²

ou bien :
a^3 + a akbar mn 2a² (am-gm)
donc
\sum a^3 akbarmn \sum a² + \sum a² - 4 akbar mn \sum a²

expert run il utilise Chebyshev ...

juste je sais tout ca mais j'ai voulus dire que Mr''expert run'' n'a pas detaillé car on ne voit plus qu'il a utilisé
Chebyshev. et!!!!! merci!!!!

ma solution au 131 : par AM-GM on a :
on pose t=a²+b²+x²+y² >= 4 .

il suffit de prouver (on pose z=\sqrt{t})

avec z>=2 ,
f'(z)=9z²-8z>0 donc f(z) >= f(2)=0 .

Problème 132 :
soit a,b,c,d>0 tel que abcd=1 , Montrer que :

younesmath2012 a écrit:

pourquoi on a 3(a^3+b^3+x^3+y^3)>=3 (a²+b²+x²+y²)???????????
il faut la montrer

Par Chebyshev:
a^3+b^3+x^3+y^3>=(1/4) (a+b+x+y)(a^2+b^2+x^2+y^2)=a²+b²+x²+y²

Oty a écrit:

Problème 132 :
soit a,b,c,d>0 tel que abcd=1 , Montrer que :

Solution du problème 132:

On pose a=1/xy ; b=1/yz; c=1/zu ; d=1/ux avec p=xy+yz+zu+ux et xyzu=1
L'inégalité est alors équivalente à :
p+ 9/p >= 25/4
Par AM-GM
P>=4 ===> (vp -3/vp)²>=1/4 ==> p+9/p>=25/4
CQFD


Problème 133:

Si

Trouver la valeur maximale de n+k.
Bonne chance.

expert_run a écrit:

Oty a écrit:

Problème 132 :
soit a,b,c,d>0 tel que abcd=1 , Montrer que :

Solution du problème 132:

On pose a=1/xy ; b=1/yz; c=1/zu ; d=1/ux avec p=xy+yz+zu+ux et xyzu=1
L'inégalité est alors équivalente à :
p+ 9/p >= 25/4
Par AM-GM
P>=4 ===> (vp -3/vp)²>=1/4 ==> p+9/p>=25/4
CQFD


Problème 133:

Si

Trouver la valeur maximale de n+k.
Bonne chance.

salut smehliya cette subtitution que vous avez poser n'est pas valable!!!!!
tu as imposé des conditions suplementaires qui n'existent pas dans l'ennoncé tels que:a+b+c+d=1/a+1/b+1/c+1/d et que a+c=1/xy+xy>=2 qui n'est pasforcemment khaseha tkoune kbar men 2......etc

donc l'exercice n'est pas resolu!!!!

oui , c'est faux expert run , révise ta substitution ...

younesmath2012 a écrit:

expert_run a écrit:

Oty a écrit:

Problème 132 :
soit a,b,c,d>0 tel que abcd=1 , Montrer que :

Solution du problème 132:

On pose a=1/xy ; b=1/yz; c=1/zu ; d=1/ux avec p=xy+yz+zu+ux et xyzu=1
L'inégalité est alors équivalente à :
p+ 9/p >= 25/4
Par AM-GM
P>=4 ===> (vp -3/vp)²>=1/4 ==> p+9/p>=25/4
CQFD


Problème 133:

Si

Trouver la valeur maximale de n+k.
Bonne chance.

salut smehliya cette subtitution que vous avez poser n'est pas valable!!!!!
tu as imposé des conditions suplementaires qui n'existent pas dans l'ennoncé tels que:a+b+c+d=1/a+1/b+1/c+1/d et que a+c=1/xy+xy>=2 qui n'est pasforcemment khaseha tkoune kbar men 2......etc

Merci pour la remarque .

histoire de continuer le jeu , voici ma solution pour le probleme 132 : ICI

Probleme 133: (own)
soit a,b,c des réel strictement positif et distincts vérifiant :
abc=1 et a-ac-ab+1 différent de 0 (de manière cyclic) .
Prouver que :

bc(a-ab-ac+1)=1-b-c+bc=(1-b)(1-c)
On peut supposer que a<b<c , Les hypothèses ==> a<1<c et b#1

ab/(1-a)(1-b)+bc/(1-b)(1-c)+ac/(1-a)(1-c)
=b[a/(1-a) + c/(1-c)]/(1-b)+ac/(1-a)(1-c)
=[a-2ac+c]/(1-a)(1-c)(ac-1)+ac/(1-a)(1-c)
=[a-3ac+c+a²c²]/ (1-a)(1-c)(ac-1)
=[(ac-1)²+(c-1)(1-a)]/ (1-a)(1-c)(ac-1)

alors |ab/(1-a)(1-b)+bc/(1-b)(1-c)+ac/(1-a)(1-c)|>=3/4

si 4(ac-1)²+4(c-1)(1-a)>= 3(1-a)(c-1)|ac-1|

cette inégalité à l'air facile mais ....

Oty a écrit:

histoire de continuer le jeu , voici ma solution pour le probleme 132 : ICI

Probleme 133: (own)
soit a,b,c des réel strictement positif et distincts vérifiant :
abc=1 et a-ac-ab+1 différent de 0 (de manière cyclic) .
Prouver que :

Solution du problème 133:
Remarquons que:
a-ac-ab+1=a(1-b)(1-c)
Alors l'inégalité est équivalente à :

Par AM-GM:
ab+ac+bc>= 3 avec égalité ssi ab=ac=bc ==> b=c=a (contradictoire à l'énoncé)
Donc ab+ac+bc -3>0
-Par symétrie de rôles et puisque abc=1 on se contente d'étudier les 2 cas suivants :
Premier cas:
a>1 et b>1 et c<1
L'inégalité est est alors équivalente à :
4(ab+ac+bc)-12>=3(1-a)(1-b)(1-c)=3(ab+ac+bc)-3(a+b+c) <==> ab+ac+bc+3(a+b+c)>=12 ce qui est vrai par AM-GM.
Deuxième cas:
a>1 ; b<1 et c<1
Dans ce cas l'inégalité est équivalente à :
4(ab+ac+bc)-12>= 3(a-1)(1-b)(1-c)=3(a+b+c)-3(ab+ac+bc) <==> 7(ab+ac+bc)>= 12+3(a+b+c)
Alors il suffit de prouver que dans ce cas 7(ab+ac+bc)>= 12+3(a+b+c)

A suivre!!!

deuxieme cas + premier cas :
f(a,b,c) = 7(ab+ac+bc)-12-3(a+b+c)
on a : A = f(a,b,c) - f(a,Vbc,Vbc) >= 0
proof :
A = (Vb-Vc)²(7a-3) >= 0 (parce que a >1)
on pose : sqrt(bc) = t
il suffit de montrer que :
f(1/t² , t , t) >= 0 equiv. 7(t² + 2/t) - 12 - 3(1/t² + 2t) equiv a : (7*t^2+8*t-3)*(t-1)^2/t^2 >=0
ce qui est vraiii !!

Probleme 134
soit a,b,c >=0 vérifiant ab+bc +ca=3
Prouver que :

expert_run a écrit:

Problème 133:[/b]
Si

Trouver la valeur maximale de n+k.
Bonne chance.

Je propose une solution:
On prends .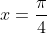
Il est connu que .
En reportant dans l'inégalité donnée, on aura .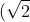
Cette inégalité s'écrit encore .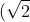
Ainsi la valeur maximale de n+k est 8.
Sauf erreurs.

oui tu as bien commencer i'exo mais il te reste de prouver que l'inegalite est atteinte pour cette valeur

chose qui vienne de la convexite de la fonction x--x^8

aymas a écrit:

chose qui vienne de la convexite de la fonction x--x^8

Je pense que non, car on doit prouver que .
Si tu penses que tu as raison, j'attends que tu détailles.

Oty a écrit:

Probleme 134
soit a,b,c >=0 vérifiant ab+bc +ca=3
Prouver que :

.

[/quote]

posons t=a+b+c et M=(a+b)(b+c)(c+a) et abc=r on a M+r=(a+b)(b+c)(c+a) +abc=(a+b+c)(ab+bc+ca)=3t
puisque [img]http://latex.codecogs.com/gif.latex?6=a(b+c)+b(c+a)+c(a+b)\geq%203\sqrt[3]{abc(a+b)(b+c)(c+a)}[/img] alors
on veut MQ: or
a suivre........!!!

er remplaçant :a=3 ;b=1 ;c=0 dans la relation on trouve 3>=4 donc cette relation est fausse
donc je vais redemarer ma solution !!!