| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 16:53 Dim 10 Avr 2011, 16:53 | |
| Solution au problème 71 :
En divisant le tout par a², et en posant x=b/a et y=c/a, l'inégalité devient équivalente à : (1+x)(1+y) >= 2sqrt(xy(1+x+y)), ou encore à (xy+(1+x+y))² >= 4xy(1+x+y), ce qui n'est qu'une application de l'inégalité (a+b)² >= 4ab. | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 16:54 Dim 10 Avr 2011, 16:54 | |
| - powerofzeta a écrit:
- Problème 71:[/b]
soient a,b,c>=0 montrer que:
 - Spoiler:
(a+b)(a+c)=a(a+b+c)+bc puis conclure
Probleme 72 : voici cadeau pour toi powerofzeta et bienvenu au forum (a TAYééb lol) Soient a,b,c,d des réels positifs tels que :  MQ :  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 18:05 Dim 10 Avr 2011, 18:05 | |
| Solution au problème 72 :
Par symétrie entre a et b, on peut supposer que b>=a.
De même par symétrie entre c et d, on peut supposer que d>=c.
Et par symétrie entre {a,b} et {c,d}, on peut supposer finalement que b>=d
L'inégalité est équivalente à : (a-c)(b-d)+(b-c)(a-d) <= 0
- Supposons que d>=a>=c :
On a alors la chaine d'inégalités : b >= d >= a >= c
En posant a=c+gamma, d=c+beta+gamma et a=c+alpha+beta+gamma, avec alpha,beta et gamma des réels positifs, et en utilisant la condition et en développant, il vient alors que : alpha² + 2alpha.beta + c.gamma + c.alpha + (alpha+beta).gamma = 0, ce qui implique que tout est nul, et donc que a=b=c=d.
Et l'inégalité est vraie pour a=b=c=d.
- Supposons que d>=c>=a :
On a alors la chaine d'inégalités : b >= d >= c >= a
Et l'inégalité est clairement vraie car négatif + négatif <= 0.
- Supposons enfin que a>=d>=c !
On a alors la chaine d'inégalités : b >= a >= d >= c
Alors on a nécessairement a=b=c=d car a²-ab+b² >= c² - cb + b² >= c² - cd + d², avec égalité ssi a=b=c=d.
Et l'inégalité est vraie pour a=b=c=d.
| |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 | |
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 18:31 Dim 10 Avr 2011, 18:31 | |
| Si ma solution est juste, alors que chacun se sente libre de proposer un nouveau problème à ma place.
Et salut tarask ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 16 Avr 2011, 18:10 Sam 16 Avr 2011, 18:10 | |
| Problème 73 :
Soient x et y des réels.
Montrer que : 3(x+y+1)² + 1 >= 3xy, et déterminer le cas d'égalité. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 16 Avr 2011, 19:42 Sam 16 Avr 2011, 19:42 | |
| Solution au problème 73:- Spoiler:
L'inégalité équivaut à : ^{2}+1\geq&space;3xy\Leftrightarrow&space;3(x^{2}+y^{2}+2xy+2x+2y+1)+1\geq&space;3xy\Leftrightarrow&space;3x^{2}+3y^{2}+3xy+6x+6y+4\geq0\Leftrightarrow&space;9x^{2}+9y^{2}+9xy+18x+18y+12\geq&space;0\Leftrightarrow&space;(9x^{2}+12x+4)+(9y^{2}+12y+4)+(9xy+6x+6y+4)\geq&space;0\Leftrightarrow&space;(3x+2)^{2}+(3y+2)^{2}+9(x+\frac{2}{3})(y+\frac{2}{3})\geq&space;0\Leftrightarrow&space;(x+\frac{2}{3})^{2}+(y+\frac{2}{3})^{2}+(x+\frac{2}{3})(y+\frac{2}{3})\geq&space;0) Ce qui est clairement vrai, égalité si x=y=-2/3
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 16 Avr 2011, 21:52 Sam 16 Avr 2011, 21:52 | |
| Problème 74 :Soit 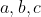 trois nombres réels positifs tel que : 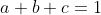 . Montrez que :  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 16 Avr 2011, 23:06 Sam 16 Avr 2011, 23:06 | |
| Se fait en deux lignes... | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 17 Avr 2011, 16:26 Dim 17 Avr 2011, 16:26 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 17 Avr 2011, 18:34 Dim 17 Avr 2011, 18:34 | |
| Solution au problème 75:- Spoiler:
Vu la symétrie on peut supposer que : 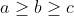 . D'autre part les suites \wedge&space;(\frac{1}{(2c+a)(2c+b)},\frac{1}{(2b+a)(2b+c)},\frac{1}{(2a+b)(2a+c)})) sont dans le même ordre, ainsi par Chebsyev, l'inégalité est équivalente à : (\sum&space;\frac{1}{(2a+b)(2a+c)})\leq&space;1) . D'autre part vu l'homégénité on peut supposer que 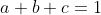 . Remarquons que : (2a+c)=2a+bc\geq&space;2\sqrt{2abc}) par AM/GM, ainsi il suffit de montrer que : \leq&space;2\frac{\sqrt{2abc}}{3}) . Maintenant en posant q=ab+ac+bc et r=abc. l'inégalité devient : ^{2}\leq&space;\frac{8}{9r}) . Et on sait que q>=9r donc il suffit de prouver que :  D'autre part nous (a+b+c)²>=3q => q<=1/3. Ainsi en étudiant cette fonction dans [0;1/3] on trouve qu'elle est négative. Le résultat en découle..
| |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 17 Avr 2011, 18:54 Dim 17 Avr 2011, 18:54 | |
| - Mehdi.O a écrit:
Solution au problème 75:
- Spoiler:
Vu la symétrie on peut supposer que : 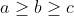 . D'autre part les suites \wedge&space;(\frac{1}{(2c+a)(2c+b)},\frac{1}{(2b+a)(2b+c)},\frac{1}{(2a+b)(2a+c)})) sont dans le même ordre, ainsi par Chebsyev, l'inégalité est équivalente à : (\sum&space;\frac{1}{(2a+b)(2a+c)})\leq&space;1) . D'autre part vu l'homégénité on peut supposer que 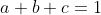 . Remarquons que : (2a+c)=2a+bc\geq&space;2\sqrt{2abc}) par AM/GM, ainsi il suffit de montrer que : \leq&space;2\frac{\sqrt{2abc}}{3}) . Maintenant en posant q=ab+ac+bc et r=abc. l'inégalité devient : ^{2}\leq&space;\frac{8}{9r}) . Et on sait que q>=9r donc il suffit de prouver que :  D'autre part nous (a+b+c)²>=3q => q<=1/3. Ainsi en étudiant cette fonction dans [0;1/3] on trouve qu'elle est négative. Le résultat en découle..
Merci de vérifier la solution . -(2a+b)(2a+c)=4a²+2ac+2ba+bc non pas 2a²+2ac+2ab+bc. Puis vers la fin j'ai pas remarqué le cas d'égalité . ..
Dernière édition par Sporovitch le Dim 17 Avr 2011, 19:07, édité 2 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 17 Avr 2011, 18:56 Dim 17 Avr 2011, 18:56 | |
| - Sporovitch a écrit:
- Mehdi.O a écrit:
Solution au problème 75:
- Spoiler:
Vu la symétrie on peut supposer que : 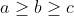 . D'autre part les suites \wedge&space;(\frac{1}{(2c+a)(2c+b)},\frac{1}{(2b+a)(2b+c)},\frac{1}{(2a+b)(2a+c)})) sont dans le même ordre, ainsi par Chebsyev, l'inégalité est équivalente à : (\sum&space;\frac{1}{(2a+b)(2a+c)})\leq&space;1) . D'autre part vu l'homégénité on peut supposer que 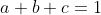 . Remarquons que : (2a+c)=2a+bc\geq&space;2\sqrt{2abc}) par AM/GM, ainsi il suffit de montrer que : \leq&space;2\frac{\sqrt{2abc}}{3}) . Maintenant en posant q=ab+ac+bc et r=abc. l'inégalité devient : ^{2}\leq&space;\frac{8}{9r}) . Et on sait que q>=9r donc il suffit de prouver que :  D'autre part nous (a+b+c)²>=3q => q<=1/3. Ainsi en étudiant cette fonction dans [0;1/3] on trouve qu'elle est négative. Le résultat en découle..
Merci de vérifier la solution . Oups ! Je m'excuse pour cette sottise ... | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 19 Avr 2011, 12:58 Mar 19 Avr 2011, 12:58 | |
| - Sporovitch a écrit:
Problème 75 (****):
a,b,c>0 MQ
 solution du problème 75:- Spoiler:
(2a+c)}\leq%20\frac{1}{3}\Leftrightarrow%203\sum%20a^2(2b+c)(2c+b)(2c+a)(2b+a)\leq%20(2a+b)(2b+a)(2b+c)(2c+b)(2c+a)(2a+c)) ce qui équivaut (après développement)à: \leq%202\sum%20a^2b^2(a^2+b^2)+4\sum%20abc^2(a^2+b^2)+5abc(a^3+b^3+c^3)) )(a-b)^2\geq%200) ce qui est clairement vrai....
je n'ai pas de problèmes à proposer actuellement! | |
|
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 21 Avr 2011, 20:48 Jeu 21 Avr 2011, 20:48 | |
| Problème 76:Soit x, y, z>0 tel que x+y+z=3 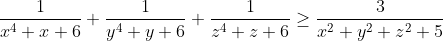 | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 29 Avr 2011, 00:50 Ven 29 Avr 2011, 00:50 | |
| Solution 76:- Spoiler:
En utilisant l'AM-HM sur le coté gauche de l'inégalité, Il suffit de montrer :
3(x²+y²+z²+5) >= (x^4+x+6+y^4+y+6+z^4+z+6) <=> 3(x²+y²+z²) >= x^4 + y^4 + z^4 + 6
Sachant que:
(x+y+z)^4 = (x²+y²+z²+2xy+2yz+2xz)² = (x²+y²+z²)²+4(xy+yz+xz)²+4(x²+y²+z²)(xy+yz+xz)
<=> x^4+y^4+z^4 = 3^4 - 2((xy)²+(yz)²+(xz)²) - (2(xy+yz+xz))² - 2(x²+y²+z²)(2(xy+yz+xz))
<=> x^4+y^4+z^4 = 3^4 - 2((xy)²+(yz)²+(xz)²)-(3²-(x²+y²+z²))²-2(x²+y²+z²)(3²-(x²+y²+z²))
Et la dernière inégalité devient équivalente à :
3(x²+y²+z²) + 2*3²(x²+y²+z²) + (x²+y²+z²)² + (3²)² + 2((xy)²+(yz)²+(xz)²)
>= 6 + 3^4 +2(x²+y²+z²) +2*3²*(x²+y²+z²)
<==> x²+y²+z² + (x²+y²+z²)² + 2((xy)²+(yz)²+(xz)²) >= 6
Qui est juste car 3(x²+y²+z²) >= (x+y+z)² <==> x²+y²+z² >= 3²/3 = 3, ce qui donne CQFD.
| |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 29 Avr 2011, 19:10 Ven 29 Avr 2011, 19:10 | |
| hay ssi elmarjani , wa sir 7fed lik chi histoire xD | |
|
  | |
jacks
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 34
Date d'inscription : 25/04/2011
 | |
  | |
louis
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 30
Date d'inscription : 31/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 25 Mai 2011, 19:12 Mer 25 Mai 2011, 19:12 | |
| Pour sauver le sujet et en attente d'une réponse au problème de jacks voici une autre: Problème 78:Montrer que: 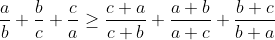 pour tous a, b, et c trois réels. | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 27 Mai 2011, 16:28 Ven 27 Mai 2011, 16:28 | |
| Solution ( 78 ) :
L'inégalité est équivaut à : Somme Cyc ( c(a-b)/(b+c)b ) >0 ( S.C désigne Somme cyclique )
==> S.C de [(a/b)-1)]/(1+(b/c)] >0 ==> S.C de [1+a/b]/[1+(b/c)] > S.C(2/1+(b/c))
Posons 1+a/b =x , y=1+b/c , z=1+c/a Il suffit de montrer que x/y+y/z+z/x > 2/x+2/y+2/z
On a 3 S.C (x/y+y/z+z/x) = S.C ( x/y+x/y+z/x) > 3 S.C( [xz/y²]^1/3) =3 S.C 2/y
[Puisque xyz >8 [ (1+a/b)(1+b/c)(1+a/c) >8 ] ] | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 27 Mai 2011, 16:33 Ven 27 Mai 2011, 16:33 | |
| Je propose cette inégalité :
Problème 79 :
Montrer que :
Sigma Cyc de : a+b/racine(a²+ab+b²) > 4[racine(ab+bc+ac)]/a+b+c +2/racine(3)
Quelqu'un peut l'écrire en LATEX slvp ! | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 27 Mai 2011, 21:32 Ven 27 Mai 2011, 21:32 | |
| - louis a écrit:
- Pour sauver le sujet et en attente d'une réponse au problème de jacks voici une autre:
Problème 78:
Montrer que: 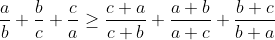 pour tous a, b, et c trois réels. pour tous a, b, et c trois réels. Faux:prendre a=2;b=3 et c=-4 | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 27 Mai 2011, 22:03 Ven 27 Mai 2011, 22:03 | |
| Il faut ajouter que a,b et c sont strictement posétifs ! | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 | |
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
