| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
Moulay INTAHA Mit3ach
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 58
Date d'inscription : 03/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 03 Juin 2011, 21:08 Ven 03 Juin 2011, 21:08 | |
| Yalah a siii INTAHA rjja3 lmakan dyalek | |
|
  | |
Moulay INTAHA Mit3ach
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 58
Date d'inscription : 03/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 03 Juin 2011, 21:09 Ven 03 Juin 2011, 21:09 | |
| machadaaach machaaaaaaadaach ta solution awldii . khhhhhhhkkhhhhhhhhhhhkkhhhhh khrjti gher flmraaaaaaaa7 | |
|
  | |
Laviecourante
Débutant
 Nombre de messages : 1 Nombre de messages : 1
Age : 64
Date d'inscription : 03/06/2011
 | |
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 04 Juin 2011, 11:29 Sam 04 Juin 2011, 11:29 | |
| éhhhh les anciens camardes de la classe MP******** comment ca va ? | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 | |
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 13 Juin 2011, 10:09 Lun 13 Juin 2011, 10:09 | |
| salut a tous - jacks a écrit:
- Problem 77:
^{\frac{2}{3}}}$\\\\) See here: http://www.artofproblemsolving.com/Forum/viewtopic.php?p=1214289#p1214289 and here: http://www.artofproblemsolving.com/Forum/viewtopic.php?p=1911570#p1911570 | |
|
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 15 Juin 2011, 22:11 Mer 15 Juin 2011, 22:11 | |
| - . a écrit:
- Laviecourante a écrit:
- . a écrit:
- Abdek_M a écrit:
- jacks a écrit:
- Problem 77:
^{\frac{2}{3}}}$\\\)
En effet cette inégalité est plus forte avec les mêmes conditions

il existe une solution sans calcul , mais avec bcp de theoremes !!
il existe wa7de bnadem sans t9chare mais avec beacoup de tkhraje l3inine !!
bien sur , ça existe ! pourquoi tu te cache ? Si vous parlez de moi ! alors me voilà je vous regarde droit dans les yeux je ne me cache pas( ah b3da matkonosh bogossin bhali  ) ! si vous avez qq chose à dire baah khrjo 3inikom wgoloha !! et nta ya dak no9ta ila bghétini vipé 3lya o ji 3andé l' Cpge Ibn Âbdoun f Khouribga ! mré7ba bwéldi ! | |
|
  | |
Mehdi.A
Maître
 Nombre de messages : 100 Nombre de messages : 100
Age : 60
Date d'inscription : 07/05/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 15 Juin 2011, 22:49 Mer 15 Juin 2011, 22:49 | |
| Non Mr Elhanci fidanci ... ci cette photo c'est celle des année 80 quand j'étais dans la classe MP************  yamat disco w bob marley  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 00:11 Ven 08 Juil 2011, 00:11 | |
| Puisque personne n'a posté de problème.Je propose cette inégalité. Problème 78:Soit a,b et c des réels strictement positifs: Prouver que:  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 00:40 Ven 08 Juil 2011, 00:40 | |
| L'inégalité est équivalente à :
1/(a+b)+1/(b+c)+1/(a+c)<=1/2[(ab+bc+ac)/(abc)]
Soit : [abc/(a+b)+abc/(b+c)+abc/(a+c)][1/(ab+bc+ac)]<=1/2
Soit : c(ab/(a+b))+a(bc/(b+c))+b(ac/(a+c))[1/(ab+bc+ac)]<=1/2
Posons : S=c(ab/(a+b))+a(bc/(b+c))+b(ac/(a+c))
Lemme
(a+b)²>=4ab <=> ab/(a+b)<=(a+b)/4
Ainsi S<= c(a+b)/4 + b(a+c)/4 + a(b+c)/4 = (2ab+2bc+2ac)/4 = (ab+bc+ac)/2
Donc : S[1/(ab+bc+ac)]<=[(ab+bc+ac)/2][1/(ab+bc+ac)]=1/2
J'ai pas d'inégalités à proposer!
| |
|
  | |
mtb
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 28/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 00:49 Ven 08 Juil 2011, 00:49 | |
| on a 1/2racinede1/ab =< 1/4a+1/4b
et on a 2racineab=<a+b donc 1/2*racine de ab>1/a+b donc 1/a+b=<1/4a+1/4b(1)
et de meme on montre que 1/b+c=<1/4b+1/4c(2) et 1/a+c=<1/4a+1/4c(3)
donc de (1)et(1)et(3) on trouve que 1/a+b+1/b+c+1/c+a=<1/2(1/a+1/b+1/c)
| |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 00:52 Ven 08 Juil 2011, 00:52 | |
| Solution problème 78:
La fonction f(x)=1/x est convexe.
D'après l'inégalité de Jensen
f((a+b)/2)<=(f(a)+f(b))/2
Donc (1/(a+b))+(1/(b+c))+(1/(c+a))<=1/2(1/a+1/b+1/c) | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 00:56 Ven 08 Juil 2011, 00:56 | |
| mtb tu peux proposer un problème. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 01:19 Ven 08 Juil 2011, 01:19 | |
| En attendant que tu proposes un problème . Je poste cet exercice. Problème 79:Soient  des réels positifs tel que:  Prouver que: 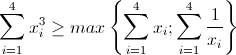 | |
|
  | |
mtb
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 28/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 12:45 Ven 08 Juil 2011, 12:45 | |
| probleme 80:
on a x+y+z=1 montrez que 0=<xy+yz+zx-2xyz=<7/27 et on a x;y;z>=0 | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 15:05 Ven 08 Juil 2011, 15:05 | |
| Solution du problème 80:- Spoiler:
On a (1-2x)(1-2y)(1-2z)=1-2(x+y+z)+4(xy+yz+zx)-8xyz=4(xy+yz+zx)-8xyz-1
Donc
xy+yz+zx-2xyz=(1/4)(1-2x)(1-2y)(1-2z)+(1/4)
Supposons que x=<y=<z
Alors
1-2x>=0 et 1-2y>=0 .Mais 1-2z peut être positif ou négatif
1cas:
1-2z>=0
On a d'après Am-Gm
xy+yz+zx-2xyz=(1/4)(1-2x)(1-2y)(1-2z)+(1/4)=<(1/4)((3-2x-2y-2z)/3)^3+(1/4)=7/27
2cas:
1-2z=<0
C'est trivial.(car (1-2x)(1-2y)(1-2z)=<1/27)
Donc il nous reste à prouver que 0=<xy+yz+zx-2xyz=(1/4)(1-2x)(1-2y)(1-2z)+(1/4)
on 2x=<2 donc 1-2x>=-1 de même pour y et z
donc
(1-2x)(1-2y)(1-2z)>=-1
D’où la conclusion.
| |
|
  | |
mr.mertasayeker
Féru
 Nombre de messages : 65 Nombre de messages : 65
Age : 29
Localisation : somewhere in morocco
Date d'inscription : 13/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 16:30 Ven 08 Juil 2011, 16:30 | |
| Solution du problème 79:
mettez:
x1=a/b x2=b/c x3=c/d x4=d/a
et puis on utilise cette lemme: si a,b>0 donc a+b>=2rac(ab)
N.B:on étudie 2 cas
sigma(x^3)>=sigma(x) et sigma(x^3)>=sigma(1/x)
| |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 16:59 Ven 08 Juil 2011, 16:59 | |
| - mr.mertasayeker a écrit:
- Solution du problème 79:
mettez:
x1=a/b x2=b/c x3=c/d x4=d/a
et puis on utilise cette lemme: si a,b>0 donc a+b>=2rac(ab)
N.B:on étudie 2 cas
sigma(x^3)>=sigma(x) et sigma(x^3)>=sigma(1/x)
mr.mertasayeker; il est mieux que vous expliquiez votre réponse. | |
|
  | |
mr.mertasayeker
Féru
 Nombre de messages : 65 Nombre de messages : 65
Age : 29
Localisation : somewhere in morocco
Date d'inscription : 13/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 17:59 Ven 08 Juil 2011, 17:59 | |
| tout d'abord je veux presenter mes sincéres excuses car le raisonnement que j'ai proposé me c'est avéré faux.Voici ce que je pense etre la solution
Pour résoudre ce problème, il faut étudier 2 cas
sigma(x^3)>=sigma(x) et sigma(x^3)>=sigma(1/x).
Le premier cas
D'apres l'inegalite de holder, on a:
16(sigma(x^3))>=(sigma(x))^3
alors sigma(x^3)>=¨(sigma(x)/4)^2*(sigma(x))>=sigma(x) (un simple IAG)
Le deuxième cas
je prefere travailler avec a b c d au lieu de x1 x2 x3 x4 (SC sigma cyclique)
on remarque que SC(1/a)=SC(abc)/abcd=SC(abc)
alors on doit demontrer que:
SC(a^3)>=SC(abc)
Ce qui est trivial par un simple réordonnement
CQFD (Sauf erreur)
Dernière édition par mr.mertasayeker le Ven 08 Juil 2011, 18:50, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 18:06 Ven 08 Juil 2011, 18:06 | |
| - expert_run a écrit:
Problème 79:
Soient  des réels positifs tel que: des réels positifs tel que:

Prouver que:
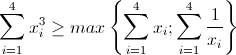 Solution du problème 79:Il faut prouver que: 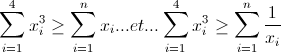 Posons:  Donc  D'après Am-Gm:  donc  Il nous reste à démontrer la deuxième inégalité. On a:  car d'après Am-Gm 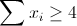 . D’où la conclusion. | |
|
  | |
mr.mertasayeker
Féru
 Nombre de messages : 65 Nombre de messages : 65
Age : 29
Localisation : somewhere in morocco
Date d'inscription : 13/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 18:14 Ven 08 Juil 2011, 18:14 | |
| belle demonstration
je veux seulement savoir si j'ai raison
| |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 18:15 Ven 08 Juil 2011, 18:15 | |
| Ok je vais voir dans 10 min. | |
|
  | |
mr.mertasayeker
Féru
 Nombre de messages : 65 Nombre de messages : 65
Age : 29
Localisation : somewhere in morocco
Date d'inscription : 13/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 18:16 Ven 08 Juil 2011, 18:16 | |
| | |
|
  | |
mtb
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 28/06/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 18:32 Ven 08 Juil 2011, 18:32 | |
| tres bien expert_run. tu peux poster un autre exercice | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 08 Juil 2011, 18:38 Ven 08 Juil 2011, 18:38 | |
| - mr.mertasayeker a écrit:
D'apres l'inegalite de holder, on a:
4(sigma(x^3))>=(sigma(x))^3
Avec holder on obtient que 16(sigma(x^3))>=(sigma(x))^3 N'est ce pas?? | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
