| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
M.Marjani
Expert sup
 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 20:01 | |
| - Dijkschneier a écrit:
- darkpseudo a écrit:
- sinon monsieur Dijk il vient de te prouver que a+b+c =< V3 et il a rectifier son post , donc ta remarque est vraiment mal placé
 Hum. Il est clair que vous n'avez pas du tout le sens de la rigueur.
En vérité, on a : (a+b+c)² >= 3(ab+ac+bc). Cela implique que : a+b+c >= sqrt(3).
Pourquoi faire croire que l'on a : a+b+c <= sqrt(3) ? Désolé, mais tes interventions sont trés offensives je ne sais pas pourquoi? .. J'ai dis qu'ils sont indépendantes.. J'ai expliqué pourquoi.. - Dijkschneier a écrit:
- M.Marjani a écrit:
- V((a²+b²+c²)/3)>=(a+b+c)/3 => a+b+c =< 3/V3*V(a²+b²+c²).
a²+b²+c²>=1 alors a+b+c=<V3 ^^. C'est des maths ça ? Non, c'est clairement ce que j'appelle du charabia. On dit "Charabia" à toutefois qu'on n'a pas compris quelque chose.. J'ai prouvé que: a+b+c =< 3/V3*V(a²+b²+c²) , dans ce cas on a besion du min(a²+b²+c²) pour dire que a+b+c =< V3 ce qui est le cas avec a²+b²+c² >= 1 D'une autre façon, on veut que 3/V3*V(a²+b²+c²) soit plus moins pour quelle serait plus forte.. Cette derniére prend sa force que si que a²+b²+c²=1 Bon oublie.. On reprend le jeu.. @Darkpseudo: Il fallait mieux de reprendre le jeu puisque la solution que j'ai présenté est juste. Probléme 50:(a,b,c,d) des réels positives. MQ: ^3\geq 16(abcd)^2*(a+b+c+d)^4) Aid Said à tous.. | |
|
| | |
marouan777
Maître
Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 20:39 | |
| - M.Marjani a écrit:
- Solution 49:
- Spoiler:
  a^2+b^2+c^2\geq ab+bc+ac\Rightarrow a^2+b^2+c^2\geq 1) (1)\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \sqrt{27}) *\sum_{i=1}^{n}(\frac{1}{a_i})\geq n^2\Rightarrow (\frac{1}{a}+\frac{1}{b}+\frac{1}{c})(a+b+c)\geq 9) Alors a+b+c>=V3 (1) Root mean inéquality:V((a²+b²+c²)/n)>=(a+b+c)/3 => a+b+c =< 3/V3*V(a²+b²+c²)Alors 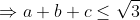 (2) Alors il suffit de demontrer: 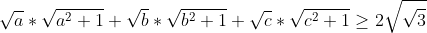 Mais: = 3\Rightarrow a^2+b^2+c^2= 1) (2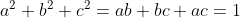)Donc:  (2)Cette égalité etteint pour 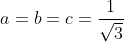 Ce qui est juste car: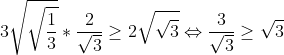 
salut Marjani!! ce qui est en rouge est juste seulement dans le cas ou a²+b²+c² est min. donc ta demonstration n'est pas complete car il te faut descuter le cas ou a²+b²+c² >1. amicalement ........... | |
|
| | |
Othman24
Féru
Nombre de messages : 43
Age : 32
Date d'inscription : 23/07/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 21:27 | |
| - Citation :
- ce qui est en rouge est juste seulement dans le cas ou a²+b²+c² est min. donc ta demonstration n'est pas complete car il te faut descuter le cas ou a²+b²+c² >1.
amicalement ........... MARJANI A RAISON ! T AS TROMPE EN CROIRE DISCUTER DE a²+b²+c² >1 . CAR SI a²+b²+c² PEUT ATTEINDRE 1 , ON DISCUTE DE CE CAS ET ON LAISSE TOMBER LES AUTRES. SI a+b+c <= 3/V3*V(1) ON AURA a+b+c <= 3/V3*V(n) TEL QUE n>1 . ALORS ON PREND MAX(a+b+c)=V3. POUR L EXO DE MARJANI: - M.Marjani a écrit:
- Probléme 50:
(a,b,c,d) des réels positives. MQ:
Aid Said à tous.. - Spoiler:
ON APPLIQUE MACLAURIN POUR x=abc,y=bcd,z=acd,t=adb: ^3\geq \frac{\sum abc*bcd*acd}{4}=\frac{a^2b^2c^2d^2\sum a}{4}) MAINTENANT SUFFIT DE DEMONTRER (b+c)(c+d)(d+a)\geq (a+b+c+d)(abc+bcd+acd+adb)) REMARQUER (b+c)(c+d)(d+a)=(ac+bc+ad+bc)(ac+bc+ab+ca)) ^2+\sum a^2(bc+bd+cd)\geq 4abcd+\sum a^2(bc+bd+cd)) (abc+bcd+cda+dab)) CE QUI ACHEVE LA SOLUTION.
J ATTEND UNE CONFIRM. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 23:22 | |
| @Othman24: Joli ! S'est confirmé... | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 23:38 | |
| - Dijkschneier a écrit:
- Mon œil. Tu fais des maths ou du charabia ?
- Dijkschneier a écrit:
- darkpseudo a écrit:
- sinon monsieur Dijk il vient de te prouver que a+b+c =< V3 et il a rectifier son post , donc ta remarque est vraiment mal placé
Hum. Il est clair que vous n'avez pas du tout le sens de la rigueur.
En vérité, on a : (a+b+c)² >= 3(ab+ac+bc). Cela implique que : a+b+c >= sqrt(3).
Pourquoi faire croire que l'on a : a+b+c <= sqrt(3) ?
Ensuite, on me fait croire que mon interrogation est puérile, et on argue de ça :
- M.Marjani a écrit:
- V((a²+b²+c²)/3)>=(a+b+c)/3 => a+b+c =< 3/V3*V(a²+b²+c²).
a²+b²+c²>=1 alors a+b+c=<V3 ^^. C'est des maths ça ? Non, c'est clairement ce que j'appelle du charabia. Qu'est-ce que c'est que ça? Si ça continue comme ça, il faudrait vraiment que l'un des modérateurs vérouille ce sujet ! Quand même un peu de respect, même si quelqu'un fasse la plus grosse faute qui peux exister dans l'une des démonstrations, il faut soigner son langage et expliquer à l'autre la source de l'erreur commise. Quand même...Des vrais matheux ne feront jamais une chose pareille ! Je vous souhaite tous Aid Moubarak Said avec tous mes voeux de bonheur et de prospérité ! | |
|
| | |
Othman24
Féru
Nombre de messages : 43
Age : 32
Date d'inscription : 23/07/2010
| | Sujet: Re: Le marathon des inégalités: Ven 10 Sep 2010, 01:10 | |
| @ KING: C EST VRAI. J AI RIEN A AJOUTE. PROBLEME 51:Demontrer la phrase suivante: > 0\sum_{cyc}\frac{a}{b^2}*(a+2b)\geq 6) AID MOUBARAK SAID ! | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Ven 10 Sep 2010, 01:34 | |
| - Othman24 a écrit:
- @ KING: C EST VRAI. J AI RIEN A AJOUTE.
PROBLEME 51:
Demontrer la phrase suivante:
AID MOUBARAK SAID ! La tournure que prend ce marathon ne me plaît pas, mais soit, essayons de garder nos limites et de se respecter mutuellement. - Spoiler:
 + \frac{b}{a^2}(b+2a) = \frac{a^2}{b^2} + \frac{b^2}{a^2} + 2(\frac{a}{b}+\frac{b}{a})) Par AM-GM :  \geq 2 + 2\times 2 = 6 \Box)
Je passe la main, je n'ai aucun problème à proposer. عيد مبارك سعيد و كل عام و أنتم بألف خير | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Ven 10 Sep 2010, 01:43 | |
| Problème 52 :Soit  un triangle non aplati. Prouver que :  | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Sam 11 Sep 2010, 00:22 | |
| Solution du problème 52 :- Spoiler:
On note  le demi-périmètre du triangle ;  le rayon du cercle circonscrit au triangle et  le rayon du cercle inscrit au triangle. On a :  Donc :      Et puisque :  L'inégalité à démontrer équivaut alors à :    Ce qui est vrai (Voir sur Théorèmes & Formules) Cet exercice est tiré de Crux Mathematicorum.
Il est bien connu que :  Et :  Ainsi l'inégalité à démontrer est forte :  | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Sam 11 Sep 2010, 01:56 | |
| Problème 53 :Soit  ,  et  les côtés d'un triangle . On note le demi-périmètre du triangle ; le rayon du cercle circonscrit au triangle et le rayon du cercle inscrit au triangle. Prouver que :  | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 00:48 | |
| Solution du problème 53 :- Spoiler:
Nous cherchons à prouver que : D'après l'inégalité de Blundon :  Il suffit alors de prouver que :   où   A partir de cela , nous pouvons déduire la chaîne d'inégalités suivante : 
Pourquoi vous ne participez plus au marathon? Est-ce que c'est dû à la difficulté des exercices ou à la rentrée scolaire ? | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 02:25 | |
| Un peu au deux , mais surtout à la deuxième ^^ , allez j'attend votre prochaine inégalité , cette fois je répondrai | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 02:46 | |
| Inchallah tu répondras à cette inégalité qui est très facile : Problème 54 :Soit , et les côtés d'un triangle . On note le demi-périmètre du triangle ; le rayon du cercle circonscrit au triangle et le rayon du cercle inscrit au triangle. Prouver que :  | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| |
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 17:23 | |
| C'est juste ; une toute petite réctification à la 6ème ligne : - Spoiler:
| |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 17:29 | |
| Oui, bonne remarque King. Deuxiéme methode: - Spoiler:
On a trouvé que: 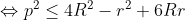 On sait que: 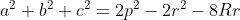 Alors il suffit de démontrer que: a^2+b^2+c^2 =< 4(2R^2+r^2) qui est juste et un résultat des recherches de King :p Une autre CQFD ^^
| |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| |
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 18:00 | |
| | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 18:10 | |
| Pour monsieur Marjani , est-t-il permit d'utiliser le théorème de Gerretsen en olympiade ?? Solution du problème 54 : - Spoiler:
En utilisant la formule de Héron plus les formule bien connu du rayon du cercle inscrit et circonscrit et après simplification aussi on arrive à l'inégalité suivante : ^{2}}{\prod%20\left%20(%20a+b-c%20\right%20)}-\prod%20\left%20(%20a+b-c%20\right%20)) Maintenant on change les variable en mettant x=a+b-c ; y=a+c-b ; z=b+c-a la contrainte devient alors a;b;c>0 et l'inégalité devient : ^{3}\leq%20\frac{\prod%20(x+y)^{2}}{%20 2xyz%20\right%20)}-%208xyz) ce qui équivaut à : ^{2}+2xyz(\sum%20x^{3})\leq%20\sum%20(xy)^{2}(x^{2}+y^{2})+2\sum%20(xy)^{3}) Ceci étant clairement juste par réordonnement ( 2 réordonnement distincts )
Dernière édition par darkpseudo le Dim 12 Sep 2010, 19:25, édité 2 fois | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 18:17 | |
| - darkpseudo a écrit:
- Pour monsieur Marjani , est-t-il permit d'utiliser l'inégalité de Gerretsen en olympiade ?? ( désolé j'ai oublier son nom XD )
Solution du problème 54 :
- Spoiler:
En utilisant la formule de Héron plus les formule bien connu du rayon du cercle inscrit et circonscrit et après simplification aussi on arrive à l'inégalité suivante : Maintenant on change les variable en mettant x=a+b-c ; y=a+c-b ; z=b+c-a la contrainte devient alors a;b;c>0 et l'inégalité devient : ce qui équivaut à : Ceci étant clairement juste par réordonnement ( 2 réordonnement distincts )
Il faut démontrer cette inégalité d'abord pour pouvoir l'utiliser en Olympiades (Facile à prouver) | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Dim 12 Sep 2010, 18:26 | |
| @ Darkpseudo: lol xD Mais j'ai proposé deux methodes ^^ et j'ai la 3 éme methode de collége si tu veux :p (Je voullais juste s'habituer avec de nouveau tehorémes que je viens de connaitre) @King: J'ai pas vu l'EX dans le forum auparavant, mais bon voiçi un autre:  | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Lun 13 Sep 2010, 12:26 | |
| Pour moi, c'est façile.
PS: Je donne ma solution de 5 lignes ce soir : ) | |
|
| | |
majdouline
Expert sup
 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Lun 13 Sep 2010, 12:51 | |
| en 5 lignes...what about 2 lignes? ^^ - Spoiler:
| |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Lun 13 Sep 2010, 13:38 | |
| | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Lun 13 Sep 2010, 14:18 | |
| - majdouline a écrit:
- en 5 lignes...what about 2 lignes? ^^
- Spoiler:
On compte la rédaction xDD Un jolie travaille Majdouline :p Voiçi ma solution ^^ - Spoiler:
Sans nuire à la generalité, on peut supposer que a+b+c=1. L'inégalité est équivalente à: 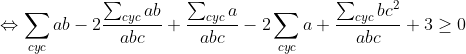 On collecte ce qui a "abc" comme dominateur: -2\sum_{cyc}ab\geq%200) \geq%202ab\Leftrightarrow%20(a-1)^2\geq%200\textup{\textit{%20Qui%20est%20juste.}}) Alors il suffit de démontrer que: 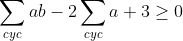 Qui est juste car: )
Ahein, qui est plus façile  A toi l'honeur de poster le prochain EX.
Dernière édition par M.Marjani le Lun 13 Sep 2010, 23:20, édité 1 fois | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Le marathon des inégalités: | |
| |
|
| | |
| | Le marathon des inégalités: | |
|
