| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
Sylphaen
Expert sup
 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Sam 28 Aoû 2010, 23:21 | |
| Solution du problème 29 : - Spoiler:
Supposons que x>y>z et posons : x=y+a=z+a+b avec a,b>0 alors l'inégo est équivalente à : 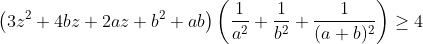 on a : 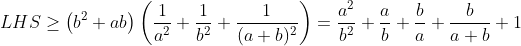 Posons a/b=t alors on a :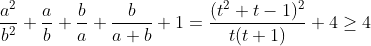 
Problème 30 : a,b,c des réels strictement positifs t.q abc=1 MQ :  | |
|
| | |
Abdek_M
Maître
Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
| | Sujet: Re: Le marathon des inégalités: Sam 28 Aoû 2010, 23:41 | |
| Salut voici une autre solution pour le problème 29 Supposons que c=min{a,b,c} Notons que  donc l'inégalité equivaut à  Mais d'aprés l'inégalité de Am-Gm on a  
Dernière édition par Abdek_M le Dim 29 Aoû 2010, 10:18, édité 1 fois | |
|
| | |
Abdek_M
Maître
Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
| | Sujet: Re: Le marathon des inégalités: Sam 28 Aoû 2010, 23:46 | |
| Pour l'exo de sylphaen il equivaut à
\sum a²/(b+c)² >3/4 apré la substitition connu ce qui est trivial | |
|
| | |
Abdek_M
Maître
Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
| |
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Dim 29 Aoû 2010, 00:04 | |
| - Abdek_M a écrit:
- Pour l'exo de sylphaen il equivaut à
\sum a²/(b+c)² >3/4 apré la substitition connu ce qui est trivial En effet, d'après l'inégalité de Cauchy-Schwartz et l'inégalité de Nesbit :  D'où la conclusion. | |
|
| | |
majdouline
Expert sup
 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Dim 29 Aoû 2010, 21:57 | |
| - Abdek_M a écrit:
Je propose cette inégalité
Montrez que pour tout réels positif a,b,c on a
|
solution du problème 31:- Spoiler:
lemme:
soit a et b des réels positifs ,, on a 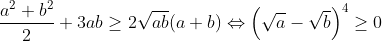 fin du lemme------------------------------------------------------------------------------------ l'inégalité est équivalente à: 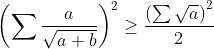 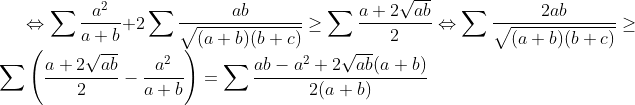 ainsi d'après lemme 1 on a : 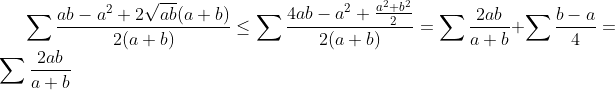 ainsi il suffit de montrer que : 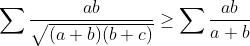 ce qui est clairement vrai par le réordonnement.....
| |
|
| | |
majdouline
Expert sup
Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| |
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Dim 29 Aoû 2010, 23:33 | |
| Solution du problème 32 :- Spoiler:
Lemme : Soit a,b,c des réels positifs alors on a : 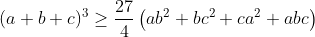 Preuve : Par cyclicité supposons que b est le réel compris en a et c alors D'après IAG on a : 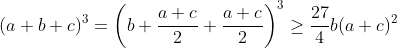 Il suffit de prouver que : 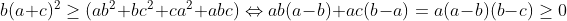 Ce qui est vrai .. Revenons à notre inégalité .. Par Hölder on a : 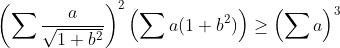 Donc il suffit de prouver que : 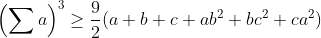 D'après la lemme précédente on a : 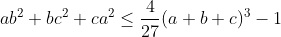 Posons a+b+c=x donc il suffit encore de prouver que : 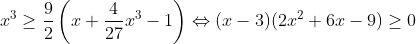 Ce qui est vrai ..
| |
|
| | |
Abdek_M
Maître
Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
| | Sujet: Re: Le marathon des inégalités: Dim 29 Aoû 2010, 23:44 | |
| Posons  et  et  donc l'inégalité est equivalente à  Par Holder on a   donc il suffit de Montrez que  ce qui est vrai puisque  | |
|
| | |
Abdek_M
Maître
Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
| | Sujet: Re: Le marathon des inégalités: Dim 29 Aoû 2010, 23:48 | |
| Sylphaen joli solution et tu as résolu l'exo avant moi a toi de poster un nouveau exo | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Dim 29 Aoû 2010, 23:52 | |
| Problème 33 : Soit a,b,c,d des réels positifs tel que :  MQ :  | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Lun 30 Aoû 2010, 00:08 | |
| Je voullais poster ma solution du Probléme 32:- Spoiler:
    De méme pour les autres, donc on aura:  Il suffit donc de démontrer que:  Qui est juste d'aprés une petite IAG, "wYchit lkhir" :p CQFD
| |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Mar 31 Aoû 2010, 00:15 | |
| - Sylphaen a écrit:
- Problème 33 :
Soit a,b,c,d des réels positifs tel que :
MQ :
Hint : - Spoiler:
Peut-on trouver X en fonction de a et b tels que l'inégalité :  Soit satisfaite pour tous a,b,>0 ?
| |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Mar 31 Aoû 2010, 20:18 | |
| Voici la solution du problème 33 : - Spoiler:
Prouvons d'abord la lemme suivante : Pour a,b>0 on a :  L'inégalité est équivalente à prouver que :  ce qui est vrai .. dès lors on a :  CQFD ..
Problème 34 : x et y et sont des réels positifs t.q : xy+yz+zx=x+y+z .montrer que :  | |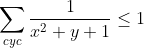
|
| | |
majdouline
Expert sup
Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Mer 01 Sep 2010, 13:00 | |
| - Sylphaen a écrit:
Problème 34 :
x et y et sont des réels positifs t.q : xy+yz+zx=x+y+z .montrer que :
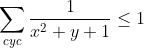 solution du problème 34:- Spoiler:
posons : 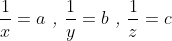 la condition devient donc : a+b+c=ab+bc+ca , et on a donc : 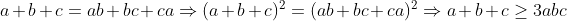 et l'inégalité à prouver : 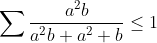 Or par l'inégalité de Cauchy Schwartz on a : 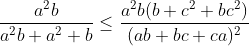 ainsi il suffit de montrer que : 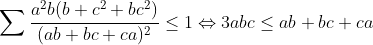 ce qui est déjà prouvé....
problème 35:soit a b et c des réels positifs tel que a+b+c=3 montrer que:  | |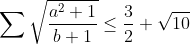
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Mer 01 Sep 2010, 15:53 | |
| Solution du problème 35 : - Spoiler:
Posons : 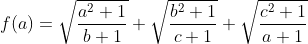 On a : =\sqrt{\frac{1}{(b+1)(a^2+1)^3}}+\frac{3}{4}\sqrt{\frac{c^2+1}{(a+1)^5}}> 0) D'où f est une fonction convexe en a .. de même avec les autres variables .. alors f est maximal quand : 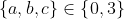 En testant les cas on remarque que f est maximal quand deux variables sont nuls .. d'où le résultat .. Sauf erreur ..
Problème 36 : Soit 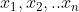 , n réels positifs tels que : \left ( \sum_{i=1}^{n}\frac{1}{x_i} \right )\leq \left ( n+\frac{1}{2} \right )^2) Montrer que :  | |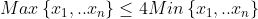
|
| | |
majdouline
Expert sup
Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Mer 01 Sep 2010, 19:39 | |
| solution du problème 36:- Spoiler:
par symétrie des rôles supposons que : 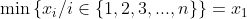 et que : 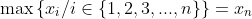 d'après l'inégalité de Cauchy Schwartz on a : 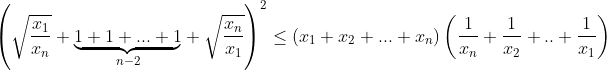 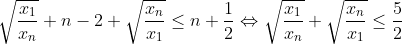 notons : 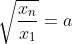 on a donc :  CQFD....
Dernière édition par majdouline le Jeu 02 Sep 2010, 17:06, édité 2 fois (Raison : erreur de frappe....) | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 02 Sep 2010, 00:39 | |
| SAlut Bravo majdouline @sylphaen : - Spoiler:
j'ai pas tres bien compris ta solution pour le probleme 35 
Dernière édition par kholoud-tetouanie le Jeu 02 Sep 2010, 22:24, édité 1 fois | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 02 Sep 2010, 14:11 | |
| @Khouloud : Le Maximum d'une fonction convexe f est atteint aux extrémités de l'intervalle d'étude. ici on a :
a,b,c £[0,3] donc le maximum est atteint quand a,b,c £ {0,3} . | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 02 Sep 2010, 21:21 | |
| Permettez moi de vous proposer un nouveau problem car je vois que c'est bloqué  il est facile .. PROblem 37: x,y,z>=0 tels que x²+y²+z²=x+y+z on pose A=xy+xz+yz et B=x²y²+x²z²+y²z² comparer A et B | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 02 Sep 2010, 22:42 | |
|
Dernière édition par M.Marjani le Ven 03 Sep 2010, 01:00, édité 1 fois | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 02 Sep 2010, 23:34 | |
| - M.Marjani a écrit:
Si vous permettez:
Solution 37:
- Spoiler:
x+y+z = x²+y²+z² <=> (x+y+z)² = (x²+y²+z²)² <=> x^4+y^4+z^4-(x²+y²+z²) = 2(A-B)
Or: x+y+z = x²+y²+z² , on pose x=x² , y=y² et z=z² alors x²+y²+z²=x^4+y^4+z^4
Ce qui montre que 2(A-B)=0 <=> A=B
il est vraiment facile mais pas à ce point la .. en fait il fallait déduire que ta solution était fausse d'apres le titre du topic parceque c'est marathon des inégalités et non pas un marathon des égalités ... A+ | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 02 Sep 2010, 23:53 | |
|
Dernière édition par M.Marjani le Ven 03 Sep 2010, 00:12, édité 1 fois | |
|
| | |
M.AlMokhtar
Débutant
Nombre de messages : 3
Age : 30
Localisation : Souk-el-Arba-du-Gharb, Morocco
Date d'inscription : 18/07/2010
| | Sujet: Re: Le marathon des inégalités: Ven 03 Sep 2010, 00:11 | |
| bonsoir
ton passage avec cauchy shwarz est malheureusement inversé
regarde ce petit contre exemple :
x=0
y=0.5
z=(1+V2 )/2
| |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Ven 03 Sep 2010, 00:41 | |
| - kholoud-tetouanie a écrit:
- M.Marjani a écrit:
Si vous permettez:
Solution 37:
- Spoiler:
x+y+z = x²+y²+z² <=> (x+y+z)² = (x²+y²+z²)² <=> x^4+y^4+z^4-(x²+y²+z²) = 2(A-B)
Or: x+y+z = x²+y²+z² , on pose x=x² , y=y² et z=z² alors x²+y²+z²=x^4+y^4+z^4
Ce qui montre que 2(A-B)=0 <=> A=B
il est vraiment facile mais pas à ce point la .. en fait il fallait déduire que ta solution était fausse d'apres le titre du topic parceque c'est marathon des inégalités et non pas un marathon des égalités ...
A+ Toutes les passages sont justes. Un petit contre exemple de ta part ne nuirer pas ^^ Méme l'exercise parait trivial... Excuse moi Imanos. | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Le marathon des inégalités: | |
| |
|
| | |
| | Le marathon des inégalités: | |
|
