| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 03 Sep 2010, 00:52 Ven 03 Sep 2010, 00:52 | |
| | |
|
  | |
M.AlMokhtar
Débutant

 Nombre de messages : 3 Nombre de messages : 3
Age : 30
Localisation : Souk-el-Arba-du-Gharb, Morocco
Date d'inscription : 18/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 03 Sep 2010, 01:02 Ven 03 Sep 2010, 01:02 | |
| bon soiir
T.joli MAJDOULINE
2eme methode:
x^4+y^4+z^4>=x²+y²+z²
PAR HOLDER : (x^4+y^4+z^4)(x+y+z)²>=(x²+y²+z²)^3=(x²+y²+z²)(x+y+z)²
CQFD
Bonne chance | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 04 Sep 2010, 02:55 Sam 04 Sep 2010, 02:55 | |
| - majdouline a écrit:
- solution du problème 37:
- Spoiler:
on a : 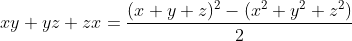 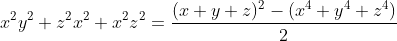  Or , par Am-Gm on a :  et :   .....
Bien joué Majdouline ! Je pense que c'est à toi de proposer le prochain exercise. - M.AlMokhtar a écrit:
- bon soiir
Bonsoir Houssam110, - Spoiler:
Ce n'est pas bon d'utiliser les photos des gens.
Houssam Akhmouch il ne fallait pas mentir sur les gens, car les photos que tu as utilisé, sont d'une personne que je connais...
Merçi de supprimer ces photos, et ne pas parler de la geule d'un autre, car çelà va attirer que des problémes. ^^
Pour finir voiçi la personne: https://www.facebook.com/#!/profile.php?id=100001122161029
( 7chouma 3lik wlahila )
Trés grave pour un futur mathématicien... A+ Houssam Akhmouch
Je veux juste dire que ce membre n'est pas moi, c'est de Houssam Akhmouch. | |
|
  | |
kholoud-tetouanie
Habitué
 Nombre de messages : 23 Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 04 Sep 2010, 23:13 Sam 04 Sep 2010, 23:13 | |
| bonsoiir mais qu'est ce qiu se passe dans ce marathon je pige plus rien  c'est quoi ce baratin je confirme aussi la solution de Majdouline !! j'espere que quelqun propose un nouveau probleme pour la continuation du jeu ... !! | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 04 Sep 2010, 23:50 Sam 04 Sep 2010, 23:50 | |
| Je propose une nouvelle règle pour le marathon : - Donner aux problèmes une approximation de difficulté par étoiles, allant d'une étoile (*) pour un problème jugé très facile, jusqu'à 5 étoiles (*****) pour un exercice jugé très difficile. Et si Majdouline ne trouve aucun inconvénient ... Problème 38 (*)Soient x,y,u,v > 0. Prouver que :  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Sep 2010, 00:50 Dim 05 Sep 2010, 00:50 | |
| solution du problème 38:- Spoiler:
problème 39:* prouver que pour tout a,b,c et d des réels positifs on a : 
Dernière édition par majdouline le Dim 05 Sep 2010, 01:43, édité 1 fois (Raison : frappe...) | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Sep 2010, 01:23 Dim 05 Sep 2010, 01:23 | |
| Solution au problème 39- Spoiler:
Il y'a une petite erreur dans l'énoncé, c'est  et non pas  . Contre-exemple : a=b=2 et b=c=1. Sinon en sachant que : -(a-b)^2 = (a+b)^2) Et en sommant, et avec AM-GM : -\sum{(a-b)^2} = \sum{(a+b)^2} \geq 4\sqrt{\prod{(a+b)}} \geq 4\sqrt{\prod{2\sqrt{ab}}} = 4\sqrt{16abcd} = 16\sqrt{abcd}) Donc -16\sqrt{abcd} \geq \sum{(a-b)^2}) La conclusion est évidente 
Je n'ai pas d'inégalités à proposer, libre à celui qui verra ce message en premier d'en poster une. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Sep 2010, 01:47 Dim 05 Sep 2010, 01:47 | |
| je propose donc celui ci ... problème 40: (*) prouver que si a b c et d des réels positifs alors:  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Sep 2010, 03:50 Dim 05 Sep 2010, 03:50 | |
| Solution 40:- Spoiler:
Probléme 41: ( **)   | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Sep 2010, 23:16 Dim 05 Sep 2010, 23:16 | |
| solution du problème 41:- Spoiler:
on procède de la même manière que Oussama... Multiplions par (abc+1) et ajoutons 3 , l'inégalité qu'on doit prouver devient donc :  - oussama1305 a écrit:
- On a :

Or par Am-Gm on a :   et en sommant ces deux inegos,on obtient facilement le résultat voulu...
| |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 06 Sep 2010, 01:32 Lun 06 Sep 2010, 01:32 | |
| Nouvelle :
À compté de maintenant, c'est majdouline qui s'occupera de la modération du marathon à ma place; donc d'instaurer de nouvelles règles ou de veiller au bon déroulement du marathon si c'est nécessaire. Bonne chance à elle. Et à sa demande, je poste un nouvel exercice : Problème 42Soient x,y,z des réels strictement positifs tels que : 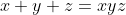 Prouver que :  | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 06 Sep 2010, 01:49 Lun 06 Sep 2010, 01:49 | |
| Solution du problème 42- Spoiler:
Un simple changement de variable :
x=tanA ; y=tanB ; z=tanC avec A+B+C=pi et ces angles sont aigus.
L'inégalité équivaut alors à sum cyc cosA<3/2 ce qui est clairement vrai
| |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 06 Sep 2010, 02:13 Lun 06 Sep 2010, 02:13 | |
| Problème 43 :Soit  ,  et  les côtés d'un triangle aigu  . On note  le rayon du cercle circonscrit au triangle et  le rayon du cercle inscrit au triangle. Prouver que :  | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 | |
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 06 Sep 2010, 21:31 Lun 06 Sep 2010, 21:31 | |
| solution du problème 43:- Spoiler:
soit a b et c les longueurs des cotés d'un triangle ,On note  le rayon du cercle circonscrit au triangle et  le rayon du cercle inscrit au triangle. on a lemme 1: lemme 2: lemme 2:  lemme 3: lemme 3: 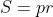 lemme 4: lemme 4: lemme 5 lemme 5 :  ------------------------------------------------------------------------------ d'après l'inégalité de Hölder on a :  en utilisant lemmes 1 , 2 et 3:  ainsi il suffit de prouver que :  Or par lemme 4 , et lemme 5 on a : 
| |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 05:53 Mar 07 Sep 2010, 05:53 | |
| - Spoiler:
Nice solution Majdouline  J'aimerais proposer une démonstration assez simple au premier lemme que tu as utilisé sans avoir recours à Al Kashi : On a :  Et  Donc :   D'où :  Ainsi :  Sinon je posterai ma solution plutard pour cet exercice, donc tu peux poster ton exercice en attendant.
| |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 | |
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 16:26 Mar 07 Sep 2010, 16:26 | |
| Bonjour Solution au probleme 44 - Spoiler:
L'inégalité équivaut à:  on pose : ab+bc+ac=q et abc=r on aura :  et  on doit montrer que :  Cas 1 : q>=1 ==>  et  DONC h(r) atteint son maximum quand r atteint son minimum et le min de r c'est 0 et dans ce cas q=1 Cas 2: 1/2=<q=<1 ==> g'(q)=12q²-24r-2=2(6q²-12r-1)>=2(4q²-1)>=1 (q²>=6r) donc :  or L'(r)=h'(r) le résultat en découle... cas 3 :q=<1/2 q²>=6r ==> 24r=<1 on remplace cela dans l'inégalité de départ que trouve que c'est clairement vrai ... CE qui finit le probleme le cas d'égalité est atteind quand a=b=1 ,c=0 ou toutes les autres permutations cycliques !!
Dernière édition par Sporovitch le Mar 07 Sep 2010, 16:46, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 20:50 Mar 07 Sep 2010, 20:50 | |
| | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 20:54 Mar 07 Sep 2010, 20:54 | |
| | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 20:58 Mar 07 Sep 2010, 20:58 | |
| Merci je savais déjà mais ça n'as rien avoir avec am-gm  c'est trivial | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 21:04 Mar 07 Sep 2010, 21:04 | |
| bonsoir  - Spoiler:
ET C'est quoi donc AM-GM  ?
| |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 21:13 Mar 07 Sep 2010, 21:13 | |
| Tu ne comptes pas poster d'inégalité ? Restons dans le vif du sujet - Le marathon - | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 21:34 Mar 07 Sep 2010, 21:34 | |
| @darkpseudo: - Spoiler:
C'est toi qui as dit que ce n'est pas AM-Gm alors je me demandé si c'était autre chose...
Probleme 45 : soient les a_i des nombres réels positifs tel que  MQ:  | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 07 Sep 2010, 23:13 Mar 07 Sep 2010, 23:13 | |
| Solution du problème 45 : - Spoiler:
Lemme : Soit x un réel positif alors on a :  Preuve :  Qui est juste par AM-GM .. En appliquant la lemme on obtient directement l'inégalité puisque : 
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
