| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
darkpseudo
Expert sup
 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 18:49 | |
| Heuu dsl de faire le méchant ( je vous déçois à chaque fois ) , - Spoiler:
mais ce que tu as fait est faux , depuis le moment ou tu à essayer de démontrer que 1+176abcd >= sum ( a+b+c)^3
parceque c'est faut , prend a= 1 et b=c=d=0 , ou alors prend a=b=1/2 bref prend des cas ou les variables tendent vers les deux limites de l'interval !!
- Spoiler:
Ensuite je dis que c'est une belle inégalité que tu nous donne là , j'avais vu une pareil et ça n'a pas été facile  ; juste une petite question , moi je pense A mettre un f(a,b,c,d) = sum abc -176/27 abcd ; puis de mettre la symétrie factoriser par le plus petit et discuter les cas , mais c'est trop long ... Je pense qu'il existe bien un lemme pouvant nous aider, mais j'arrive toujours pas à le trouver , sur ce je vais manger ^^
| |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 18:52 | |
| - darkpseudo a écrit:
- Heuu dsl de faire le méchant ( je vous déçois à chaque fois ) ,
- Spoiler:
mais ce que tu as fait est faux , depuis le moment ou tu à essayer de démontrer que 1+176abcd >= sum ( a+b+c)^3
parceque c'est faut , prend a= 1 et b=c=d=0 , ou alors prend a=b=1/2 bref prend des cas ou les variables tendent vers les deux limites de l'interval !!
Non darkpseudo:p J'ai dis que: \neq 0) (cas trivial, il suffit de le démontrer dans une ligne ^^)  Je suis sure qu'elle est prouvable méme par IAG.. Je compléte ma soluc dans le délai de 30 min ) Pas forcément juste : (1/4,1/4,1/2,0) Mais la supposition permet d'éviter ce cas. Bonne ftour à tous ^^
Dernière édition par M.Marjani le Mer 08 Sep 2010, 20:12, édité 3 fois | |
|
| | |
majdouline
Expert sup
 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 19:13 | |
| - M.Marjani a écrit:
- Solution 48:
que: 
Qui est façile à prouver avec un théoréme...  prend comme contre exemple a=b=c=1/3 et d=0 veuillez vérifier bien vos solution avant de les poster marjani!! ça se répète bcp ! | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 19:57 | |
| PS: Cette solution est fausse, je renonce... (Shit.... IAG Grrr...)
Dernière édition par M.Marjani le Mer 08 Sep 2010, 22:05, édité 3 fois | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 21:33 | |
| Encor faux : - Spoiler:
a=1/2 b=1/4 c=d=1/8 dans ce cas a^2+b^2+c^2+d^2 >=1/4 et ce n'est pas le seul cas je t'assur , ensuite ce qui est en haut est aussi faux , même avec la condition !
Ne te précipite pas mon ami ^^'
Solution de l'exercice 48 : - Spoiler:
Posons =%20\frac{1}{27}-\sum%20abc%20+%20\frac{176abcd}{27}) Soit a>=b>c>=d donc d =< 1/4 \geq%200) aussi on aura : f(a;b;c;d) >= f(d;d;d;d) >=0l'égalité ayant lieu quand a=b=c=d=1/4 ceci car min(f(a;b;c;d)=f(d;d;d;d) vu que min ( a;b;c;d) = d on en conclu que f(a;b;c;d) >=0 Sauf erreur ^^
Dernière édition par darkpseudo le Jeu 09 Sep 2010, 16:17, édité 3 fois | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 23:22 | |
| - darkpseudo a écrit:
- Spoiler:
a=1/2 b=1/4 c=d=1/8 dans ce cas a^2+b^2+c^2+d^2 >=1/4 et ce n'est pas le seul cas je t'assur , ensuite ce qui est en haut est aussi faux , même avec la condition !
Ne te précipite pas mon ami ^^'
J'ai rien compris de cette exo xDD Regarde: abc+acd+abd+bcd =< 1/27 + (176abcd)/27 <=> ab(c+d)+cd(a+b)=< RHS a+b+c+d=1 Donc ab(1-(a+b))+cd(1-(c+d)) =< RHS <=> ab-ab(a+b)+cd-cd(c+d) =< RHS (a,b,c,d) £ IR+ donc ab(a+b)>=ab et cd(c+d)>=cd !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Ce qui est juste, et l'inégalité est trés trivial ! | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Mer 08 Sep 2010, 23:32 | |
| - M.Marjani a écrit:
- darkpseudo a écrit:
- Spoiler:
a=1/2 b=1/4 c=d=1/8 dans ce cas a^2+b^2+c^2+d^2 >=1/4 et ce n'est pas le seul cas je t'assur , ensuite ce qui est en haut est aussi faux , même avec la condition !
Ne te précipite pas mon ami ^^'
J'ai rien compris de cette exo xDD
Regarde:
abc+acd+abd+bcd =< 1/27 + (176abcd)/27
<=> ab(c+d)+cd(a+b)=< RHS
a+b+c+d=1 Donc ab(1-(a+b))+cd(1-(c+d)) =< RHS
<=> ab-ab(a+b)+cd-cd(c+d) =< RHS
(a,b,c,d) £ IR+ donc ab(a+b)>=ab et cd(c+d)>=cd !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Ce qui est juste, et l'inégalité est trés trivial ! ce qui est en rouge contient une faute pour que ab(a+b) >=ab et cd(c+d) >= cd Il faut que a+b >=1 et c+d >= 1 ce qui est contradictoire avec la condition a+b+c+d = 1 | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 00:02 | |
| | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 00:04 | |
| - darkpseudo a écrit:
- ce qui est en rouge contient une faute pour que ab(a+b) >=ab et cd(c+d) >= cd
Il faut que a+b >=1 et c+d >= 1 ce qui est contradictoire avec la condition a+b+c+d = 1 Si. Je viens d'émetter juste une remarque, comme ça tu peux résoudre l'exo Tu supposes 4 fois au max: ghir 2 fois, car si a+b>=1 ou c+d>=1 tu auras 4 soluc à l'inégalité (0,0,0,1);(1,0,0,0);(0,1,0,0);(0,0,1,0) :p Deux cas: (P): a<1-b ou (P'): c<1-d : * a<1-b : a+b+c+d=1 <=> 2d(a+b+c)+(a+b+c)²+d²=1 <=> 2d(1-d)+(1-d)²+d²=12dc+c²+d²<1 <=> (c+d)² < 1 => c+d<1 * ou c<1-d : Donc (P) => (P') !! @King: C'est bien parler :p | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 00:18 | |
| Non , tu commet une faute , a+b>=1 et b+c>=1 ==> a+b+c+d>=2 chose qui est fausse, donc ce n'est même pas la peine de continuer la démo de cette manière , ensuite vu que personne n'est là pour confirmer ma démo je me permet de poster : problème 49 : soit a,b,c>0 et ab+ac+bc = 1 Prouver que  | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 00:25 | |
| - darkpseudo a écrit:
- Non , tu commet une faute , a+b>=1 et b+c>=1 ==> a+b+c+d>=2 chose qui est fausse, donc ce n'est même pas la peine de continuer la démo de cette manière , ensuite vu que personne n'est là pour confirmer ma démo je me permet de poster
Non! J'ai dis a+b>=1 ou c+d>=1 ... Enfin c'est juste une remarque. | |
|
| | |
King
Maître
Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 00:31 | |
| Il serait bien meilleur de rédiger une nouvelle démonstration et qui soit complète pourqu'on puisse valider si c'est juste ou réfuter si ça contient une ou des fautes. | |
|
| | |
majdouline
Expert sup
Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 01:01 | |
| - darkpseudo a écrit:
Solution de l'exercice 48 :
- Spoiler:
Posons  Soit a>=b>c>=d donc d =< 1/4  aussi on aura : f(a;b;c;d) >= f(d;d;d;d) l'égalité ayant lieu quand a=b=c=d=1/4 or dans ce cas f(d;d;d;d) = 0 est maximum et f(a;b;c;d)=0 est minimum on en conclu que f(a;b;c;d) >=0 Sauf erreur ^^
- Spoiler:
premièrement je crois que tu veux dire : =%20\frac{1}{27}-4%20d^{3}+%20\frac{176d^{4}}{27}\geq%200 ) sinon prouve ce qui est en rouge ,on veut une solution complète .......
| |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 01:38 | |
| Ok même si je ne voit pas ou est le problème : - Spoiler:
parceque 4d^3(44d/27 -1) =< 1/27 remplace d par 1/4 tu aura l'égalité !! Sinon pour ce qui est en rouge c'est juste parceque , f(d;d;d;d) = minf(a;b;c;d) vu que d = min(a;b;c;d) Sinon je ne voie pas comment je pourrais expliquer plus 
| |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 02:07 | |
| - darkpseudo a écrit:
- Ok même si je ne voit pas ou est le problème :
- Spoiler:
parceque 4d^3(44d/27 -1) =< 1/27 remplace d par 1/4 tu aura l'égalité !! Sinon pour ce qui est en rouge c'est juste parceque , f(d;d;d;d) = minf(a;b;c;d) vu que d = min(a;b;c;d) Sinon je ne voie pas comment je pourrais expliquer plus
=\frac{1}{27}(4d-1)(44d^3-16d^2-4d-1)) La fonction  est négative sur [0,1/4], de même pour d|->4d-1. Donc ta fonction est positive. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 15:42 | |
| Solution 49:- Spoiler:
  a^2+b^2+c^2\geq ab+bc+ac\Rightarrow a^2+b^2+c^2\geq 1) (1)\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \sqrt{27}) *\sum_{i=1}^{n}(\frac{1}{a_i})\geq n^2\Rightarrow (\frac{1}{a}+\frac{1}{b}+\frac{1}{c})(a+b+c)\geq 9) Alors a+b+c>=V3 (1) Root mean inéquality:V((a²+b²+c²)/n)>=(a+b+c)/3 => a+b+c =< 3/V3*V(a²+b²+c²) Alors 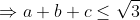 (2) Alors il suffit de demontrer: 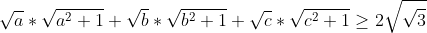 Mais: = 3\Rightarrow a^2+b^2+c^2= 1) (2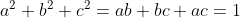)Donc:  (2)Cette égalité etteint pour 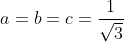 Ce qui est juste car: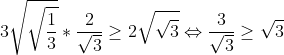 
Dernière édition par M.Marjani le Jeu 09 Sep 2010, 18:20, édité 4 fois | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 16:12 | |
| - oussama1305 a écrit:
- darkpseudo a écrit:
- Ok même si je ne voit pas ou est le problème :
- Spoiler:
parceque 4d^3(44d/27 -1) =< 1/27 remplace d par 1/4 tu aura l'égalité !! Sinon pour ce qui est en rouge c'est juste parceque , f(d;d;d;d) = minf(a;b;c;d) vu que d = min(a;b;c;d) Sinon je ne voie pas comment je pourrais expliquer plus
La fonction est négative sur [0,1/4], de même pour d|->4d-1.
Donc ta fonction est positive.
Heu merci de la précision , je m'étais tromper en factorisant , mais ceci ne fait que rendre l'inégo encor plus facile vu qu'on aura f(a;b;c;d)>=f(d;d;d;d)>=0 ^^ C'est éditer | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 16:56 | |
| De la demande de Darkpseudo: Probléme 50:(a,b,c,d) des réels positives. MQ: ^3\geq 16(abcd)^2*(a+b+c+d)^4)
Dernière édition par M.Marjani le Jeu 09 Sep 2010, 17:38, édité 1 fois | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 17:31 | |
| Stop M.Marjani. Revoir tout. On a pas a+b+c <= 3. On a a+b+c >= 3. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 18:02 | |
| - Dijkschneier a écrit:
- Stop M.Marjani. Revoir tout. On a pas a+b+c <= 3. On a a+b+c >= 3.
Monsieur Dijkcshneier, Ils sont indépendantes ^^ Prouver Max(a+b+c)=V3 dans le cas ou ab+bc+ac=1 (a,b,c)>0 est façile... méme avec methode de collége. Exemple: Voir: Root mean inéquality: V((a1+a2+...+an)/n) >= (a1+a2+...+an)/n V((a²+b²+c²)/3)>=(a+b+c)/3 => a+b+c =< 3/V3*V(a²+b²+c²) a²+b²+c²>=1 alors a+b+c=<V3 ^^
Dernière édition par M.Marjani le Jeu 09 Sep 2010, 18:22, édité 1 fois | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 18:16 | |
| Mon œil. Tu fais des maths ou du charabia ? | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 18:24 | |
| - Dijkschneier a écrit:
- Mon œil. Tu fais des maths ou du charabia ?
Si tu veux d'autres explications? J'ai pas malheureusement, il te faudrait revoir les cours du collége pour mieux comprendre... désolé....... oO Je me demande pourquoi ses postes doubles de critiques banales..... Pour rien... Je veux arréter de spammer dans le sujet... Brefs... j'ai éditer ma solution pour le bien du marathon. - M.Marjani a écrit:
- De la demande de Darkpseudo:
le probléme courant:
Probléme 50:
(a,b,c,d) des réels positives. MQ:
Dernière édition par M.Marjani le Jeu 09 Sep 2010, 18:30, édité 1 fois | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 18:29 | |
| Heuu , svp pas d'insultes , j'ai vraiment pas envi que ce sujet tourne au vinaigre ; sinon monsieur Dijk il vient de te prouver que a+b+c =< V3 et il a rectifier son post , donc ta remarque est vraiment mal placé | |
|
| | |
Dijkschneier
Expert sup
Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 18:45 | |
| - darkpseudo a écrit:
- sinon monsieur Dijk il vient de te prouver que a+b+c =< V3 et il a rectifier son post , donc ta remarque est vraiment mal placé
Hum. Il est clair que vous n'avez pas du tout le sens de la rigueur. En vérité, on a : (a+b+c)² >= 3(ab+ac+bc). Cela implique que : a+b+c >= sqrt(3). Pourquoi faire croire que l'on a : a+b+c <= sqrt(3) ? Ensuite, on me fait croire que mon interrogation est puérile, et on argue de ça : - M.Marjani a écrit:
- V((a²+b²+c²)/3)>=(a+b+c)/3 => a+b+c =< 3/V3*V(a²+b²+c²).
a²+b²+c²>=1 alors a+b+c=<V3 ^^. C'est des maths ça ? Non, c'est clairement ce que j'appelle du charabia. | |
|
| | |
darkpseudo
Expert sup
Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
| | Sujet: Re: Le marathon des inégalités: Jeu 09 Sep 2010, 19:18 | |
| Je ne vais pas m'éloigner du sujet , comme certain le fond si bien ; donc je propose qu'on m'apporte une autre démonstration de cette inégalité et qu'on oubli tout ça.
La preuve de monsieur Marjani est considéré comme fausse . | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Le marathon des inégalités: | |
| |
|
| | |
| | Le marathon des inégalités: | |
|
