| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 08 Mar 2011, 00:04 Mar 08 Mar 2011, 00:04 | |
| Bien joué majdouline  en utilisant la substition  et les transformations de Ravi l'inégalité devient equivalente avec les variable a,b,c à  Or d'après l'inégalité de Holder   Ainsi il suffit de Montrer que  en supposons sans perte de généralité que a+b+c=1 et posons ab+bc+ca=q et abc=r il suffit donc de prouver que  ou aussi  ce qui peut se réecrire comme  Or d'aprés Schur  donc  et comme  alors le resultat en découle je presente ici la solution par Cauchy Schawrz dont je parlais en utilisant les identités   alors il suffit de Montrer que  Or d'après l'inégalité de Cauchy Schwarz   donc il suffit de prouver que  ou aussi  ce qui equivaut à  ce qui est vrai | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 08 Mar 2011, 12:37 Mar 08 Mar 2011, 12:37 | |
| Salam Je propose cette inégalité ! a,b,c >0 et abc=1 MQ : 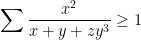 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 08 Mar 2011, 13:24 Mar 08 Mar 2011, 13:24 | |
| - Dijkschneier a écrit:
- darkpseudo a écrit:
- Solution :
- Spoiler:
Supposons sans nuir à la généralité du problème que : a+b+c=1 et que a>=b>=c d'après Chebychev on a ( la fonction sin étant strictement croissante sur [0,Pi/2] on a :  Il suffit donc de montrer que :  Qui est vrai en utilisant la Jensen sur la fonction cos ( convexe ) dans l'interval [0,Pi/2] .
Convexe ?! Grosse bétise je m'en excuse . | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 08 Mar 2011, 15:05 Mar 08 Mar 2011, 15:05 | |
| Désolé il y a une petite faute , au lieu de a,b,c J'ai du mettre x , et z Je m'excuse ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 08 Mar 2011, 18:59 Mar 08 Mar 2011, 18:59 | |
| Je propose : Soient 0 < c <= b <= a. Montrer que : 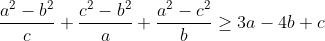
Dernière édition par Dijkschneier le Mer 09 Mar 2011, 15:41, édité 3 fois | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 12:54 Mer 09 Mar 2011, 12:54 | |
| Je pense qu'il y'a une petite erreur , puisqu'on a 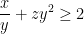 ça donne 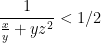 Alors t'as pas le droit de minorer ! ou alors Je n'ai pas compris ce passage ! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 13:05 Mer 09 Mar 2011, 13:05 | |
| Mais il y a un moins qui remet l'ordre initial  | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 13:13 Mer 09 Mar 2011, 13:13 | |
| ah oui ! J'ai pas fait attention a ce moins ! désolé amigo !  | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 15:02 Mer 09 Mar 2011, 15:02 | |
| - Dijkschneier a écrit:
- Je propose :
Soient 0 < c <= b <= a.
Montrer que : 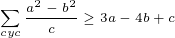 . . Si je me trompe pas : en posant b=c on aura pas 0 dans LHS et dans RHS 3(a-b) ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 15:39 Mer 09 Mar 2011, 15:39 | |
| Pardon  J'ai corrigé l'énoncé. | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 16:41 Mer 09 Mar 2011, 16:41 | |
| - Dijkschneier a écrit:
- Je propose :
Soient 0 < c <= b <= a.
Montrer que : 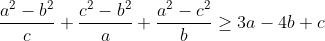 Notons que l'inégalité équivaut à :  Remarquons que 3(a-b)+3(a-c)+3(c-b)>=5a-6b+c donc il suffira de montrer que :  ou encore  Ce qui est vrai car elle equivaut à :  CQFD! sauf erreur ! PROBLEME: SOIENT a,b,c des côtés d'un triangle tels que a²+b²+c²=3Trouver la valeur minimale de l'expression A=ab+bc+ac-2abc | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 21:25 Mer 09 Mar 2011, 21:25 | |
| - Sporovitch a écrit:
PROBLEME:
SOIENT a,b,c des côtés d'un triangle tels que a²+b²+c²=3
Trouver la valeur minimale de l'expression A=ab+bc+ac-2abc Voici une solution bruteforce : On se propose de montrer que la valeur minimale est 1. Posons a=x+y et cycliquement, puis p=x+y+z, q=xy+xz+yz et r=xyz. La condition veut dire : p²-q = 3/2 L'inégalité à prouver est équivalente à : p²-2pq+q+2r-1 >= 0 (*) (*) <=> -2p^3 + 2p² + 3p - 5/2 + 2r >= 0 <=> r >= p^3 - p² - 3p/2 + 5/4 L'inégalité de Schur donne : r >= (p^3 - 2p)/3 Il suffit de montrer que (p^3 - 2p)/3 >= p^3 - p² - 3p/2 + 5/4, ce qui est équivalent à sqrt(5)/2 <= p <= 3/2. L'inégalité bien connue p² >= 3q nous donne p <= 3/2 (et aussi q<=3/4), et donc on a fini dans le cas p >= sqrt(5)/2 Sinon, si p <= sqrt(5)/2, alors (*) est équivalente à (p-q)² + q - q² + 2r - 1 >= 0, ou encore à (p-p²+3/2)² + q - q² + 2r >= 1 Tenant compte de p <= sqrt(5)/2, il est aisé de vérifier que (p-p²+3/2)² >= 1.3680... et que q - q² >=0 (rappelons que q <= 3/4), et donc on a fini dans ce cas également. Et puisque on a un cas d'égalité pour a=b=c=1, alors 1 est en effet la valeur minimale. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 21:36 Mer 09 Mar 2011, 21:36 | |
| Problème : Soient x_1, x_2, ..., x_n des réels positifs tels que leur produit soit égal à 1. Montrer que : }%20\geq%20\frac{n}{2}) | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 09 Mar 2011, 22:24 Mer 09 Mar 2011, 22:24 | |
| -> Solution : L'inégo est équivalente à : 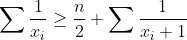 On a : (D'après AM-GM ) 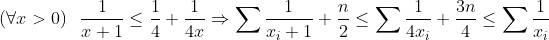 Problème : Soient 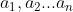 des réels qui vérifient 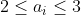 pour i=1,2,..n . Démontrer que : 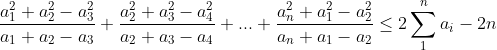 | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 15 Mar 2011, 20:44 Mar 15 Mar 2011, 20:44 | |
| voila un exercice de IOM 2008 ( b l'anglais ga3  ) : (i) If  ,  and  are three real numbers, all different from  , such that  , then prove that  . (With the  sign for cyclic summation, this inequality could be rewritten as  .) (ii) Prove that equality is achieved for infinitely many triples of rational numbers  ,  and  . | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 15 Mar 2011, 21:52 Mar 15 Mar 2011, 21:52 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Ven 01 Avr 2011, 17:09 Ven 01 Avr 2011, 17:09 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 05 Avr 2011, 14:08 Mar 05 Avr 2011, 14:08 | |
| - mizmaz a écrit:
- Bensouda a écrit:
- voila un exercice de IOM 2008 ( b l'anglais ga3
 ) : ) :
(i) If  , ,  and and  are three real numbers, all different from are three real numbers, all different from  , such that , such that  , then prove that , then prove that
 . .
(With the  sign for cyclic summation, this inequality could be rewritten as sign for cyclic summation, this inequality could be rewritten as  .) .)
(ii) Prove that equality is achieved for infinitely many triples of rational numbers  , ,  and and  . . (i) Posons 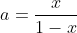 , , 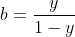 et et 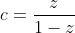 . .
Nous avons : 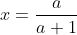 , , 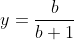 et et 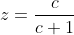 . .
L'inégalité équivaut à 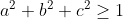 et la condition à et la condition à (b+1)(c+1)}=1) ce qui équivaut à ce qui équivaut à 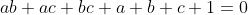
Donc l'inégalité équivaut à :
^2-2(ab+ac+bc)\geq%201\Leftrightarrow%20(1+(ab+ac+bc))^2-2(ab+ac+bc)\geq%201\Leftrightarrow%20(ab+ac+bc)^2\geq%200)
Ce qui est vrai. Donc l'inégalité de départ est vraie. Bien. Pour ne pas laisser ce bon jeu en chômage, je propose une solution pour la deuxième question. (ii) Prove that equality is achieved for infinitely many triples of rational numbers . L'égalité est réalisé si a²+b²+c²=1 en considérant le changement de variables qu'a fait Mizmaz . D'autre part :
abc=(a+1)(b+1)(c+1) <==> ab+bc+ac+a+b+c=-1 <==> 2cyc (ab) + 2cyc (a) = -cyc (a²) - 1 <==> (a+b+c+1)²=0
donc a+b+c=-1 Ou encore ab+bc+ac+a+b+c=-1 <==> (a+b+c)²=(1+ab+bc+ac)² <==> ab+bc+ac=0
Donc la résolution du système des équations en gras en Z permet de conclure l'infinité des rationnels x,y,z . | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 06 Avr 2011, 03:22 Mer 06 Avr 2011, 03:22 | |
| - darkpseudo a écrit:
- Solution :
- Spoiler:
Supposons sans nuir à la généralité du problème que : a+b+c=1 et que a>=b>=c d'après Chebychev on a ( la fonction sin étant strictement croissante sur [0,Pi/2] on a :  Il suffit donc de montrer que :  Qui est vrai en utilisant Jensen sur la fonction cos ( convexe ) dans l'interval [0,Pi/2] .
Problème :
a,b,c >= 0 et sum(a^2)=3 MQ 12+9abc>=sum(ab)
Ta solution est fausse car  Je rapelle que la question est de démontrer que :  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 15:54 Dim 10 Avr 2011, 15:54 | |
| Le prochain problème sera noté 70 et ainsi de suite... Problème 70 :Soient a,b,c et d des réels positifs tels que a+b+c+d=1. Montrer que : (c+d)}%20\leq%20\frac{1}{\sqrt{ab}}+\frac{1}{\sqrt{cd}}) | |
|
  | |
powerofzeta
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 32
Date d'inscription : 05/04/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 16:23 Dim 10 Avr 2011, 16:23 | |
| salùt:  puis conclure. Problème 71:soient a,b,c>=0 montrer que: 
Dernière édition par powerofzeta le Dim 10 Avr 2011, 16:38, édité 1 fois | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 | |
  | |
powerofzeta
Débutant
 Nombre de messages : 2 Nombre de messages : 2
Age : 32
Date d'inscription : 05/04/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 16:48 Dim 10 Avr 2011, 16:48 | |
| s'il vous plait pour que le marathon reste un marathon si quelqu'un veut poster une solution il est préférable de poster un problème aussi,merci d'avance.  | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 10 Avr 2011, 16:52 Dim 10 Avr 2011, 16:52 | |
| - powerofzeta a écrit:
- s'il vous plait pour que le marathon reste un marathon si quelqu'un veut poster une solution il est préférable de poster un problème aussi,merci d'avance.
 OK cheef !! " a TAAAAAAAAAAAYEEB" !! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
