| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
Le criminelle
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 35
Date d'inscription : 20/06/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 03 Mar 2011, 17:43 Jeu 03 Mar 2011, 17:43 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 03 Mar 2011, 18:19 Jeu 03 Mar 2011, 18:19 | |
| | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 03 Mar 2011, 19:42 Jeu 03 Mar 2011, 19:42 | |
| x+1/x>2 n'est vraie que si x appartient a IR*+ tu fais ainsi (Vx-1/Vx)>=0 alors x+1/x>2 C.Q.F.D amicalement  | |
|
  | |
Le criminelle
Habitué
 Nombre de messages : 27 Nombre de messages : 27
Age : 35
Date d'inscription : 20/06/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 11:08 Sam 05 Mar 2011, 11:08 | |
| est ceque si (Vx-1/Vx)>=0 est vrai alors x+1/x >2 est vrai ?
sinon , qui peut m'aider a montrer cette inegalité : x+4>4Vx | |
|
  | |
achraf_djy
Expert grade1

 Nombre de messages : 401 Nombre de messages : 401
Age : 33
Localisation : Rabat
Date d'inscription : 01/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 11:19 Sam 05 Mar 2011, 11:19 | |
| OUII si (Vx-1/Vx)>=0 est vrai alors x+1/x >2 , x+4>4Vx avec x>=0
<==> (Vx-2)²>=0 | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 17:36 Sam 05 Mar 2011, 17:36 | |
| Montrez Que :1/a²(b+c) + 1/b²(a+c) + 1/c²(a+b) > 3/2 ( a,b,c > 0 et abc=1 ) | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 17:48 Sam 05 Mar 2011, 17:48 | |
| a²(b+c) est toute divisee ou seulement a²? | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 18:09 Sam 05 Mar 2011, 18:09 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 19:13 Sam 05 Mar 2011, 19:13 | |
| - Bensouda a écrit:
- Montrez Que :1/a²(b+c) + 1/b²(a+c) + 1/c²(a+b) > 3/2 ( a,b,c > 0 et abc=1 )
Je présente l'indice suivant: La résolution de cette inégalité semble impossible sans recourir à l'inégalié démontré ici: https://mathsmaroc.jeun.fr/t17447-another-inequality. Et je donne la solution complète plus tard, si personne ne le ferait avant moi. | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 19:38 Sam 05 Mar 2011, 19:38 | |
| Il n'y a pas de solutions sans recourir a cette inégalité ? | |
|
  | |
MohE
Expert grade2

 Nombre de messages : 317 Nombre de messages : 317
Age : 31
Localisation : Waterloo, Canada
Date d'inscription : 17/05/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 20:35 Sam 05 Mar 2011, 20:35 | |
| Il exsite bien sur, il existe toujours une autre solution, tu peux par exemple le voire comme suit:
1/[a²(b+c)] + 1/[b²(a+c)] + 1/[c²(a+b)] = bc/[a(b+c)] + ac/[b(a+c)] + ab/[c(a+b)], et donc si tu pose x=ab , y=bc et z=ca, ton problème équivaut à prouver que: x/(y+z) + y/(z+x) + z/(x+y) >= 3/2 ca doit être plus facile d'ici n'est ce pas? | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 20:55 Sam 05 Mar 2011, 20:55 | |
| - Bensouda a écrit:
- Montrez Que :1/a²(b+c) + 1/b²(a+c) + 1/c²(a+b) > 3/2 ( a,b,c > 0 et abc=1 )
Par Cauchy-Schwarz:  D'où :  | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 21:03 Sam 05 Mar 2011, 21:03 | |
| - MohE a écrit:
- Il exsite bien sur, il existe toujours une autre solution, tu peux par exemple le voire comme suit:
1/[a²(b+c)] + 1/[b²(a+c)] + 1/[c²(a+b)] = bc/[a(b+c)] + ac/[b(a+c)] + ab/[c(a+b)], et donc si tu pose x=ab , y=bc et z=ca, ton problème équivaut à prouver que: x/(y+z) + y/(z+x) + z/(x+y) >= 3/2 ca doit être plus facile d'ici n'est ce pas? oui c'est ca effectivement puis tu utilises l'inegalite de Nesbit et le resultat en decoule. merci mohe amicalement  | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 22:05 Sam 05 Mar 2011, 22:05 | |
| Voilà je propose une inégalité que j'ai crée , qui est plus forte que celle de Nesbit , la difficulté est moyenne pour pouvoir avancer le marathon  Soient a,b et c des réels strictement positifs. Montrer que  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 05 Mar 2011, 22:40 Sam 05 Mar 2011, 22:40 | |
| - Abdek_M a écrit:
Soient a,b et c des réels strictement positifs. Montrer que

- Spoiler:
l'inégalité à prouver est équivalente à: (ab+bc+ca)}\geq%202) Or d'après l'inégalité de Cauchy Schwartz on a : ^2}{2(ab+bc+ca)}) il suffit donc de montrer que : ^3+9abc}{(a+b+c)(ab+bc+ca)}\geq%204) ce qui est l'inégalité de Schur.....
Soit ABC un triangle , AB=c AC=b et BC=a, p son demi périmètre ,MQ: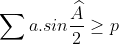 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 18:46 Dim 06 Mar 2011, 18:46 | |
| Solution : - Spoiler:
Supposons sans nuir à la généralité du problème que : a+b+c=1 et que a>=b>=c d'après Chebychev on a ( la fonction sin étant strictement croissante sur [0,Pi/2] on a :  Il suffit donc de montrer que :  Qui est vrai en utilisant Jensen sur la fonction cos ( convexe ) dans l'interval [0,Pi/2] .
Problème : a,b,c >= 0 et sum(a^2)=3 MQ 12+9abc>=sum(ab)
Dernière édition par darkpseudo le Dim 06 Mar 2011, 21:25, édité 1 fois | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 20:33 Dim 06 Mar 2011, 20:33 | |
| x+y+z=1 et x,y,z >0 Déterminez la valeur min de : 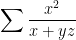 | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 20:56 Dim 06 Mar 2011, 20:56 | |
| Voila la solution de ton problème et la prochaine fois ne pose pas de problème avant d'avoir résolu celui posté avant stp : - Spoiler:
Par C.S on a : 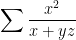  Or on sait bien que :  et donc :  CQFD
| |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 21:15 Dim 06 Mar 2011, 21:15 | |
| - darkpseudo a écrit:
- Voila la solution de ton problème et la prochaine fois ne pose pas de problème avant d'avoir résolu celui posté avant stp :
- Spoiler:
Par C.S on a : 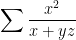  Or on sait bien que :  et donc :  CQFD
est elle atteinte quand x=y=z=1/3?? | |
|
  | |
Bensouda
Féru
 Nombre de messages : 67 Nombre de messages : 67
Age : 30
Date d'inscription : 28/02/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 21:16 Dim 06 Mar 2011, 21:16 | |
| ah désolé ! Je m'excuse ! ce sont mes premiers Jours sur le forum ! | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 21:18 Dim 06 Mar 2011, 21:18 | |
| - yasserito a écrit:
- darkpseudo a écrit:
- Voila la solution de ton problème et la prochaine fois ne pose pas de problème avant d'avoir résolu celui posté avant stp :
- Spoiler:
Par C.S on a : 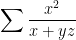  Or on sait bien que :  et donc :  CQFD
est elle atteinte quand x=y=z=1/3?? Bein oui je présume . | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 21:19 Dim 06 Mar 2011, 21:19 | |
| - darkpseudo a écrit:
- Solution :
- Spoiler:
Supposons sans nuir à la généralité du problème que : a+b+c=1 et que a>=b>=c d'après Chebychev on a ( la fonction sin étant strictement croissante sur [0,Pi/2] on a :  Il suffit donc de montrer que :  Qui est vrai en utilisant la Jensen sur la fonction cos ( convexe ) dans l'interval [0,Pi/2] .
Problème :
a,b,c >= 0 et sum(a^2)=3 MQ 12+9abc>=sum(ab)
Je pense que c'est :  Sinon, c'est trivial. Solution :Avec :  On remarque :  Donc:  Rien à proposer. | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 06 Mar 2011, 22:48 Dim 06 Mar 2011, 22:48 | |
| Bravo Mademoiselle Majdouline  Moi je suis allé un peu loin , ta solution est plus jolie et plus simple !! Voilà celle ci est aussi vrai , pour tout a,b,c>0 ,  D'après ma création il existe une simple solution avec Cauchy Schwarz, mais elle n'est pas difficile | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 07 Mar 2011, 13:23 Lun 07 Mar 2011, 13:23 | |
| - darkpseudo a écrit:
- Solution :
- Spoiler:
Supposons sans nuir à la généralité du problème que : a+b+c=1 et que a>=b>=c d'après Chebychev on a ( la fonction sin étant strictement croissante sur [0,Pi/2] on a :  Il suffit donc de montrer que :  Qui est vrai en utilisant la Jensen sur la fonction cos ( convexe ) dans l'interval [0,Pi/2] .
Convexe ?! | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 07 Mar 2011, 23:05 Lun 07 Mar 2011, 23:05 | |
| - Abdek_M a écrit:
Voilà celle ci est aussi vrai , pour tout a,b,c>0 ,

Bonsoir  - Spoiler:
=\sum%20\left%20(\frac{a-b}{2(b+c)}+\frac{a-c}{2(b+c)}%20\right%20)%20=\sum%20\left%20(%20\frac{a-b}{2(b+c)}+\frac{b-a}{2(c+a)}%20\right%20)=\sum%20\frac{(a-b)^2}{2(b+c)(c+a)}) l'inégalité à démontrer est donc équivalente à : ^2}{2(b+c)(c+a)}\geq%202-\frac{6(ab+bc+ca)}{(a+b+c)^2}=\sum%20\frac{(a-b)^2}{(a+b+c)^2}) ^2(a^2+b^2-c^2)}{(b+c)(c+a)}\geq%200\Leftrightarrow%20\sum%20(a-b)^2(a+b)(a^2+b^2-c^2)\geq%200) en supposant que a≥b≥c on a : \Rightarrow%20S_{b},S_{b}+S_{c}\geq%200) et que: +2c^3+bc^2+ac^2=(a+b)(a-b)^2+2c^3+bc^2+ac^2\geq%200) ce qui achève la preuve ....
P.S. le problème suivant est encore en jeu : - majdouline a écrit:
Soit ABC un triangle , AB=c AC=b et BC=a, p son demi périmètre ,MQ:
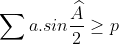
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
