Le marathon des inégalités:

http://canhang2007.wordpress.com/2009/12/03/inequality-86-t-q-anh/
ici il ya beaucoup d'inegalite

bon je propose un problème pour avancer le marathon:

a,b,c>0 tel que: ab+ac+bc+abc>=4. Montrer que: [/quote]
voici la reponsevrai

younesmath2012 a écrit:

voici la reponsevrai

Wow j'ai eu la meme idéé que can mais son finish est bien meilleur , merci pour ce lien Mr Younes il est tres intéressant

Oty a écrit:

¨ Problème 125 soit a,b,c > 0 , Prouver que :

tu peut nous donner une ideé svp car je suis bloqué!!! merci!!!

younesmath2012 a écrit:

tu peut nous donner une ideé svp car je suis bloqué!!! merci!!!

essayez d'éliminer une variable ...

tu peut nous donner la reponse Mr ''oty'' ;ma9dartch njawb 3liha merci d'avance

Daccord Mr . Younes , Demain Inchaa Allah

merci bcp

Oty a écrit:

¨ Problème 125 soit a,b,c > 0 , Prouver que :

Soient p,q et r les quantités habituelles, on a:



...

Et je n'ai pas de problème intéressant à proposer. Que chacun se sente libre d'en proposer un à ma place.

tbarkellah 3lik Mr ''ali-mes'' very good methode 3ajbatni bezzaf

je propose l'exercice suivant: a,b,c>=0 MQ:


elle est joli aussi.

younesmath2012 a écrit:

je propose l'exercice suivant: a,b,c>=0 MQ:


elle est joli aussi.

ma solution : on pose , a=x+1 , b=y+1 , c=z+1 , avec x,y,z >=-1 l'inégalité est equivalente a : x²+y²+z²+xyz >= 0 si x,y,z >= 0 , alors l"inégalité est prouver , maintenant il suffit de la montrer pour x,y,z appartenant a [-1,0] dans ce cas posant x=-u , y=-v , z=-w l'inégalité est equivalente a uvw=< u²+v²+w² avec 0=<u,v,w=<1 ainsi uvw =< uv or puisque u²-uv+v²+w²=(u-v)²\2 + (u²+v²)\2 + w² >= 0 , l'inégalité est démontrer . égalité si u=v=w=0 => a=b=c=1 .

Mr''oty'' votre demonstration est incomplette tu as dit le cas x,y,z>=0 puis le cas
-1=<x,y,z<=0 c'est pas les seules cas il faut continuer......

younesmath2012 a écrit:

Mr''oty'' votre demonstration est incomplette tu as dit le cas x,y,z>=0 puis le cas
-1=<x,y,z<=0 c'est pas les seules cas il faut continuer......

oui il suffit d'ajouter le cas ou xy >=0 et -1=<z =<0 alors :
x²+y²+z²+xyz >= x²-xy+y²+z² >=0

Valeur max trouver la valeur max de : quand : x²+y²+z²=1 .

il faut d'abord la montrer cad MQ: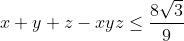
http://www.wolframalpha.com/

oui c'est bien la valeur max , mais il faut le montrer ...

Oty a écrit:

Valeur max trouver la valeur max de : quand : x²+y²+z²=1 .

Solution pour le problème 127:
On pose p=x+y+z ; q=xy+yz+zx : r=xyz
Par Schur:

on a:

On pose :

avec q=<1
Ainsi

D'où
x+y+z-xyz =<f(q)=<f(1)
Donc

Avec égalité quand x=y=z=(v3)/3

Problème 128:
Soient a;b;c>=0 avec a+b+c=2
prouver que :

Solution au problème 128:

Par Schur:

Problème 129:
x,y,z>0. Montrer que:

ali-mes a écrit:

Problème 129:
x,y,z>0. Montrer que:

Solution:

Par C-S:

Alors il suffit de prouver que:

Par application de Schur:

CQFD.


Problème 130:
Soient a;b;c des réels positifs. Montrer que :

c'est facile en utilise cauchy-shwartz

car

[url=pb131]http://latex.codecogs.com/gif.latex?a,b,x,y\geq%200...tq...a+b+x+y=4...MQ:....%203(a^{3}+b^{3}+x^{3}+y^{3})\geq%202(a^{2}+b^{2}+x^{2}+y^{2})+4[/url]

La solution de younessmath2012 est correcte. Je propose un nouveau problème:
Problème 132:
Soient et deux entiers naturels non nuls.
Prouvez que .
Bonne chance.
P.S: Je prie younessmath2012 d'éditer l'un de ses derniers messages car ils sont identiques, pour proposer le problème 131...