| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 14 Juil 2012, 20:59 Sam 14 Juil 2012, 20:59 | |
| - younesmath2012 a écrit:
- Oty a écrit:
- Bon pour continuer le Marathon voici la solution du Problème 108 : on transforme l'inégalité sous la forme :
}{a^2+bc}+t=\frac{b(c+a-b)}{b^2+ca}+p=\frac{c(a+b-c)}{c^2+ab}\geq{0}) , on pose a=< b,c , puisque (b+c-a) >=0 il suffit de prouver que : t+p >=0 equivalent a : (b-c)²(b-a)(c-a)+2a²bc+ab²c+abc² >=0 ce qui est vrai .. , on pose a=< b,c , puisque (b+c-a) >=0 il suffit de prouver que : t+p >=0 equivalent a : (b-c)²(b-a)(c-a)+2a²bc+ab²c+abc² >=0 ce qui est vrai ..
verifi si c'est juste ce qui est ecrit !!!!!!!!!! car j'ai pas compris!!!!!! merci d'avance il me semble que : }{a^{2}+bc}=1+\frac{a(b+c-a)}{a^{2}+bc}) . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 | |
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 28 Juil 2012, 23:09 Sam 28 Juil 2012, 23:09 | |
| - Oty a écrit:
- Problème 109: soit a,b,c >=0 vérifiant : a+b+c+ab+ac+bc=6 . Montrer que : 4(a+b+c)+abc >= 13 .
Solution problème 109:Soit f(a;b;c)=4(a+b+c)+abc et g(a;b;c)=0 tel que g(a;b;c)=6-a-b-c-ab-ac-bc l(a;b;c;y)=f(a+b+c)+yg(a;b;c) Cherchons les 4-tuple (a,b;c;y) satisfaisant les conditions: dl/da=dl/db=dl/dc=dl/dy=0 On obtient ainsi le système suivant: 4+bc-y(1+b+c)=0 4+ac-y(1+a+c)=0 4+ab-y(1+a+b)=0 a+b+c+ab+ac+bc=6 ===> a=b=c ou bien deux éléments de {a;b;c} sont égaux à y Pour a=b=c on trouve que a=b=c=1 donc f(a;b;c)=13 Pour a=b=y on trouve que 4+y²=y(1+2y)<==>y²+y-4=0==> y=(sqrt(17)-1)/2 et ainsi c=(5sqrt(17)-17)/34 Et ainsi f(a;b;c)=(11sqrt(17)-19)/2>13 En conclusion f(a;b;c) admet 13 comme minimum quand a=b=c=1 | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 29 Juil 2012, 03:22 Dim 29 Juil 2012, 03:22 | |
| Problème 120:
Soient a_1;a_2;...;a_n des réels positifs appartenant à l'intervalle [0;2] tel que
a_1+a_2+....+a_n=1
Trouver la valeur maximale de S= (a_1)²+(a_2)²+....+(a_n)² | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 01 Aoû 2012, 21:19 Mer 01 Aoû 2012, 21:19 | |
| Je ne suis pas sûr de ce que je vais écrire. Vu que a_k >= 0 pour tout k£ (0;1;2;...;n) et que sigma(a_k)=1 il s'en suit que 0=<a_k<= 1 pour tout k£ (0;1;2;...;n). Alors  Et c'est clair que l'inégalité a lieu si tout les a_i sauf un seul sont égaux à 0 alors que l'autre est égale à 1. J'attends des confirmations. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 01 Aoû 2012, 23:29 Mer 01 Aoû 2012, 23:29 | |
| - konica a écrit:
- Je ne suis pas sûr de ce que je vais écrire.
Vu que a_k >= 0 pour tout k£ (0;1;2;...;n) et que sigma(a_k)=1 il s'en suit que 0=<a_k<= 1 pour tout k£ (0;1;2;...;n).
Alors 
Et c'est clair que l'inégalité a lieu si tout les a_i sauf un seul sont égaux à 0 alors que l'autre est égale à 1.
J'attends des confirmations. Bon c'est juste même si j'ai fait une faute dans l'énoncé de l'exercice car sigma(a_k)=n et non 1 mais bon c'est pas grave vous pouvez l'essayer dans ce cas. A toi de poster le problème suivant. | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 00:10 Jeu 02 Aoû 2012, 00:10 | |
| Je n'ai pas un problème en ce moment. Si quelqu'un veut poster quelque chose, il le fera. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 01:19 Jeu 02 Aoû 2012, 01:19 | |
| Problème 121 : soit a,b,c > 0 tel que : a+b+c=1 , Prouver que : \geq{25})
Dernière édition par Oty le Jeu 02 Aoû 2012, 01:32, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 01:23 Jeu 02 Aoû 2012, 01:23 | |
| - Oty a écrit:
- Problème 121 : soit a,b,c > 0 tel que : a+b+c=1 , Prouver que :
\geq{25}) L'énoncé est faux !!!!! | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 01:28 Jeu 02 Aoû 2012, 01:28 | |
|
Dernière édition par konica le Jeu 02 Aoû 2012, 01:43, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 01:33 Jeu 02 Aoû 2012, 01:33 | |
| c édité ! faute de frappe  | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 20:53 Jeu 02 Aoû 2012, 20:53 | |
| Solution au problème 121 : On doit montrer que  Considérons la fonction :  Et la contrainte :  On forme une autre fonction L tel que :  On calcule les dérivées partiales de L :    Ces dérivations sont égales à zéro, alors il suffit de résoudre le système :  La première et deuxième équation sont égales, alors :  Ce qui veut dire que soit a=b soit a+b+ab²=0, cette dernière équation est impossible puisque a et b sont strictement positifs. De la même façon on obtient à la fin a=b=c=1/3 En substituant ces valeurs dans la fonctions P on aura 25 comme valeur maximale. Et je n'ai pas de problèmes à proposer. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 21:47 Jeu 02 Aoû 2012, 21:47 | |
| Problème 122 : soit a,b,c>=0 , Montrer que : ^3}) | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 22:09 Jeu 02 Aoû 2012, 22:09 | |
| Solution du problème 122: (Je ne suis encore pas sûr)  L'inégalité est homogène, supposons que a+b+c=1 On a : LHS >= 0 par IAG Il suffit de prouver que : b+c-2a <= 0 équivalente à a+b+c-3a <= 0 équivalente à a>=1/3>0 EDIT:Et si a=0, l'inégalité est équivalente à 4(b^3+c^3)>= (b+c)^3 ce qui est vrai par Holder. (a^3+b^3)(1+1)(1+1)>= (a+b)^3
Dernière édition par konica le Dim 05 Aoû 2012, 00:04, édité 1 fois | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 22:28 Jeu 02 Aoû 2012, 22:28 | |
| non c'est faux on peux avoir a < b+c\2
Dernière édition par Oty le Jeu 02 Aoû 2012, 22:45, édité 2 fois | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 22:35 Jeu 02 Aoû 2012, 22:35 | |
| - konica a écrit:
- Solution du problème 122:
(Je ne suis encore pas sûr) 
L'inégalité est homogène, supposons que a+b+c=1
On a : LHS >= 0 par IAG
Il suffit de prouver que : b+c-2a <= 0 équivalente à a+b+c-3a <= 0 équivalente à a >= 1/3 ce qui est vrai puisque a>=0
J'attends une confirmation. Pourquoi ? "Si a=0 alors l'inégalité est équivalente à 4(b^3+c^3) >= (b+c)^3 ce qui est juste d'après Hölder." Ma solution au problème 122:L'inégalité est équivalente à :  D'après IAG: 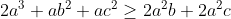 et d'après l'inégalité du réordonnement : 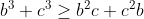 . Sauf erreurs . Problème 123:a,b et c des réels >0 tel que a+b+c=3. Prouver que : 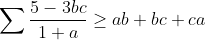 Bonne chance.
Dernière édition par Geo le Jeu 02 Aoû 2012, 23:05, édité 1 fois | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 22:42 Jeu 02 Aoû 2012, 22:42 | |
| - Geo a écrit:
- konica a écrit:
- Solution du problème 122:
(Je ne suis encore pas sûr) 
L'inégalité est homogène, supposons que a+b+c=1
On a : LHS >= 0 par IAG
Il suffit de prouver que : b+c-2a <= 0 équivalente à a+b+c-3a <= 0 équivalente à a >= 1/3 ce qui est vrai puisque a>=0
J'attends une confirmation. Pourquoi ?
Parce que j'ai supposé que a+b+c=1. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Jeu 02 Aoû 2012, 22:45 Jeu 02 Aoû 2012, 22:45 | |
| @konica - Oty a écrit:
- non c'est faux on peux avoir a < b+c\2
, Bravo Geo  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 04 Aoû 2012, 16:39 Sam 04 Aoû 2012, 16:39 | |
| - Oty a écrit:
- Problème 121 : soit a,b,c > 0 tel que : a+b+c=1 , Prouver que :
\geq{25}) on a : ( sigma(1/a))*(a+b+c) sup= 9 et d'apres chebycheve 48(ab+ac+bc) sup= 48*1/3(a+b+c)² =16 alors : LHS sup= 25 | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Sam 04 Aoû 2012, 23:33 Sam 04 Aoû 2012, 23:33 | |
| - killua 001 a écrit:
48(ab+ac+bc) sup= 48*1/3(a+b+c)² =16
C'est faux !! - Geo a écrit:
Problème 123:
a,b et c des réels >0 tel que a+b+c=3. Prouver que :
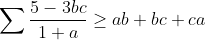
Bonne chance. (p=a+b+c=3, q=ab+ac+bc et r=abc) L'inégalité à démontrer est équivalente à: 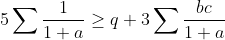 (1+b)\geq%20q(1+a)(1+b)(1+c)+3\sum%20bc(1+b)(1+c)) \geq%20q(p+q+r+1)+3%20(q+pq-3r+q^2-2pr)) \geq%20q(q+r+4)+3%20(q^2+4q-9r)) 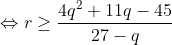 (4q-9)}{27-q}=f(q)) Et on a: 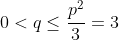 . Si: 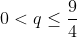 , donc: \leq%200<%20r) . Si: 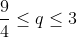 : On a: =\frac{4(q-3)(4q-9)}{3(q-27)}%20\geq%200\Rightarrow%20f(q)\leq%20\frac{4q-9}{3}) . Et par Schur: (p=3) 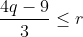 , donc: ) . CQFD... Je n'ai pas de problèmes à proposer, que chacun se sente libre pour proposer un... | |
|
  | |
konica
Maître

 Nombre de messages : 141 Nombre de messages : 141
Age : 29
Localisation : Tétouan
Date d'inscription : 19/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Aoû 2012, 00:49 Dim 05 Aoû 2012, 00:49 | |
| Problème 124 : a,b,c,d sont des nombres réels strictement positifs tels que : abcd=1 M.Q :  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Aoû 2012, 03:38 Dim 05 Aoû 2012, 03:38 | |
| - konica a écrit:
- Problème 124 :
a,b,c,d sont des nombres réels strictement positifs tels que : abcd=1
M.Q :  C'est le problème 12, bon je propose un problème pour avancer le marathon: a,b,c>0 tel que: ab+ac+bc+abc>=4. Montrer que: ^2(b+c)}\leq&space;\frac{3}{8}) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Aoû 2012, 17:17 Dim 05 Aoû 2012, 17:17 | |
| - ali-mes a écrit:
a,b,c>0 tel que: ab+ac+bc+abc>=4. Montrer que: ^2(b+c)}\leq&space;\frac{3}{8}) Ma solution : soit un t appartenant a ]0,1] vérifiant : ab+bc+ca+tabc=4\t ce ''t'' existe car ab+bc+ca+abc >= ab+bc+ca+tabc=4\t >= 4 , d'ou on posant x=ta , y=tb , z=tc on a : xy+yz+xz+xyz=4 , l"inégalité est équivalente a : ^2(y+z)}\leq{\frac{3}{8}}) d'apres la nouvelle condition on peut effectuer le changement de variable suivant : , en utilisant (x+1)² >= 4x on a : (c+a)(a+b)}{8(2a+b+c)(b^2+c^2+ac+ab)}) ainsi il suffit de prouver que : ce qui est vrai . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Aoû 2012, 17:23 Dim 05 Aoû 2012, 17:23 | |
| ¨ Problème 125 soit a,b,c > 0 , Prouver que : +\frac{8}{a+b+c}\geq{\frac{6}{\sqrt{ab+bc+ca}}}) | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 05 Aoû 2012, 17:41 Dim 05 Aoû 2012, 17:41 | |
|
Dernière édition par younesmath2012 le Dim 05 Aoû 2012, 17:50, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
