Exercice de logique

Salam,

n € N.
Sachant que 3n+1 est un carré parfait.
Prouvez que n+1 est la somme de 3 carrés parfaits.

Au plaisir

salam

classique

................

Montrez la méthode svp !!

Voici un autre exercice :
Soit t € IR + et n € IN*
1) prouvez que (1+t^n)(1+t)<2(1+t^(n+1))
2) prouvez que ((1+t)/2)^n<(1+t^n)/2
3) prouvez que (1+t^n)(1+t)^n<2^n(1+t^(2n))

Salut,
Pour le premier on a p² = 3n + 1
Donc il existe un q de Z : p = 3q + 1 <=> p² = 9q² + 6q + 1
donc 3n = 9q² + 6q <=> n=3q² + 2q
<=> n+1 = q²+ 2q + 1 + q² + q²
<=> n+1 = (q+1)² + (q)² + (q)²
CQFD.

Mehdi.O a écrit:

Voici un autre exercice :
Soit t € IR + et n € IN*
1) prouvez que (1+t^n)(1+t)<2(1+t^(n+1))
2) prouvez que ((1+t)/2)^n<(1+t^n)/2
3) prouvez que (1+t^n)(1+t)^n<2^n(1+t^(2n))

Pour la premiére il faut dire plutot que t>1 .. Sinon prends 0=<t=<1 et tu vas trouver qu'elle est fausse : ) Un autre remarque que n£IN n'est pas nécessaire, il suffit de dire que n£IR*+ et n>=1 ... : )
Bon, voiçi ma solution:

1+t^{n+1}+t^n+t<2+2t^{n+1} <=> t^{n+1}-t^n-t+1>0 <=> t^n(t-1)-t+1>0 <=> t^n>1 Ce qui est juste car t>1 est n>0

Pour la deuxiéme: Aussi fausse... Prendre par contre exemple: t£IR+ et n=1 .. n>=2 est obligatoir. Aussi t différent de 1 ....

insrolled a écrit:

Salut,
Pour le premier on a p² = 3n + 1
Donc il existe un q de Z : p = 3q + 1

Pas forcément. On n'a pas : 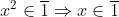. Contre-exemple : x² = 25 = 3*8 + 1, mais x = 3*1 + 2
On a : .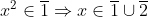
Tu devras ainsi faire une disjonction de cas pour assurer la consistance de ton raisonnement.
Voici comment compléter la preuve de insrolled :
On a p² = 3n+1. Ainsi, p=3q+1 ou p=3q+2.
- Le cas où p=3q+1 a déjà été étudié par insrolled.
- Soit donc p=3q+2.
p = 3q + 2 => p²=9q²+12q+4
=> 3n+1 = 9q²+12q+4
=> 3n = 9q² + 12q + 3
=> n = 3q² + 4q + 1
=> n + 1 = 3q² + 4q + 2 = (q+1)² + (q+1)² + q²

meme si il est facile mais c'est un assez beau exo merci pour ^^

M.Marjani a écrit:

Mehdi.O a écrit:

Voici un autre exercice :
Soit t € IR + et n € IN*
1) prouvez que (1+t^n)(1+t)<2(1+t^(n+1))
2) prouvez que ((1+t)/2)^n<(1+t^n)/2
3) prouvez que (1+t^n)(1+t)^n<2^n(1+t^(2n))

Pour la premiére il faut dire plutot que t>1 .. Sinon prends 0=<t=<1 et tu vas trouver qu'elle est fausse : ) Un autre remarque que n£IN n'est pas nécessaire, il suffit de dire que n£IR*+ et n>=1 ... : )

Elle n'est fausse que si t=1. Elle est encore vraie si 0<=t<1. Car l'inégalité est équivalente à .

Dijkschneier a écrit:

Voici comment compléter la preuve de insrolled :
On a p² = 3n+1. Ainsi, p=3q+1 ou p=3q+2.
- Le cas où p=3q+1 a déjà été étudié par insrolled.
- Soit donc p=3q+2.
p = 3q + 2 => p²=9q²+12q+4
=> 3n+1 = 9q²+12q+4
=> 3n = 9q² + 12q + 3
=> n = 3q² + 4q + 1
=> n + 1 = 3q² + 4q + 2 = (q+1)² + (q+1)² + q²

Bien.

M.Marjani a écrit:

Mehdi.O a écrit:

Voici un autre exercice :
Soit t € IR + et n € IN*
1) prouvez que (1+t^n)(1+t)<2(1+t^(n+1))
2) prouvez que ((1+t)/2)^n<(1+t^n)/2
3) prouvez que (1+t^n)(1+t)^n<2^n(1+t^(2n))

Pour la premiére il faut dire plutot que t>1 .. Sinon prends 0=<t=<1 et tu vas trouver qu'elle est fausse : ) Un autre remarque que n£IN n'est pas nécessaire, il suffit de dire que n£IR*+ et n>=1 ... : )
Bon, voiçi ma solution:

1+t^{n+1}+t^n+t<2+2t^{n+1} <=> t^{n+1}-t^n-t+1>0 <=> t^n(t-1)-t+1>0 <=> t^n>1 Ce qui est juste car t>1 est n>0

Pour la deuxiéme: Aussi fausse... Prendre par contre exemple: t£IR+ et n=1 .. n>=2 est obligatoir. Aussi t différent de 1 ....

Je voulais dire que c'est <= non <.
inférieur ou égal pas strictement inférieur.

Voici ma solution :
1) On a pour t € IR+
(t-1)(t^n-1)>0
donc 2t^(n+1)+2>t^n+t+1+t^(n+1)
donc 2(t^(n+1)+1)>(t^n+1)(t+1).
2)
Démontrons le par récurence:
-> n=1 donc (1+t)/2<=(1+t)/2 Vraie.
-> Supposons que l'expression est vraie pour n.
Donc pour n+1 :
On a:
((1+t)/2)^n<(1+t^n)/2
donc ((1+t)/2)^(n+1)<(1+t)(1+t^n)/4<2(t^(n+1)+1)/4=(t^(n+1)+1)/2
Donc P(n+1) est vraie.
Donc P(n) est vraie pour tout n€ IN.
3)
On a ((1+t)/2)^n<(1+t^n)/2
(1+t)^n(1+t)/2^n<(1+t^n)²/2
et on sait que 1+t^(2n)>(1+t^n)²/2
donc (1+t^n)(1+t)^n/2^n<1+t^(2n)
et donc
(1+t^n)(1+t)^n<2^n(1+t^(2n)) pour tout n € IN.
Et voilà

Et pour le premier excellent Dijkschneier et insrolled !

Mais pour le cas p=3q ??

Salut.
Puisque 3 ne divise pas p²,3 ne divise pas p d'où p=/=3q.