| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
+20n.naoufal sadaso maths-au-feminin Hamouda geom Azerty1995 yasserito helloall Mehdi.A Mehdi.O Meded l'intellectuelle yasmine boubou math konica Nayssi az360 expert_run upsilon ali-mes 24 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Lun 11 Juil 2011, 00:13 Lun 11 Juil 2011, 00:13 | |
| Et c'est un P6, même les chinois et les russes n'arrivent pas à le résoudre -_-"
" | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Lun 11 Juil 2011, 00:35 Lun 11 Juil 2011, 00:35 | |
|  c'est à dire?... (je n'étais pas au courant au début que c'est un P6, d'ailleurs même si c'est le cas ça reste un problème à résoudre comme tous autres...!!) Donc tu veux dire quoi?...(Pas la peine de....) En tout cas, la réponse tu la trouves ici http://www.animath.fr/IMG/pdf/cours-eqfonc.pdf exercice 19 comme expert_run l'a indiqué (Merci à lui). Et la fonction que tu dois trouver dans tous les sens à la fin alors est la suivante: =1-%5Cfrac{1}{2}x^{2}) Amicalement  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Lun 11 Juil 2011, 00:44 Lun 11 Juil 2011, 00:44 | |
| Kaj mima , le faite que tu trouve la même fonction que celle écrite sur le cour ne veut po dire que tu as résolu l'exo , si tu lis bien la solution proposé dans le cours tu pourra savoir prq ta démarche est incorrecte .
Amicalement | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Lun 11 Juil 2011, 00:46 Lun 11 Juil 2011, 00:46 | |
| Je demande le pourquoi tout simplement!...Et montrz moi la faute afin de la rectifier sinon moi je n'y trouve pas l'erreur. Et Merci! | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Lun 11 Juil 2011, 09:03 Lun 11 Juil 2011, 09:03 | |
| Premièrement, je savais pas qu'il s'agit d'un problème d'IMO. Mais quand j'ai vu la solution, je l'ai trouvé abordable. Donc pour mettre fin à vos disputes, je vous propose ces trois exos: - le premier (très intéressant), déjà proposé par Mehdi.O dans la rubrique géométrie mais pas encore résolu. Je crois que Mehdi.O n'a pas le droit à répondre pour cet exo (qu'après qu'un autre forumiste répond), mais tkt, je suis sûr que Problème 49 va te plaire  . . - Le deuxième, encore de la géométrie. - Le troisième, pour nos amis géométrie-phobes: un très joli problème d'algèbre et faisable. Problème 48: Soit ABC un triangle rectangle en A. Notons M le milieu de [AC] et P sa projection orthogonale sur (BC).Soit X un point sur [AP] de telle sorte que (BX) est perpendiculaire sur (AP), et notons Y et Z les points d'intersection de [BX) et [BM) avec le cercle circonscrit de ABC. Montrez que M est le centre du cercle circonscrit du triangle XYZ. Problème 49:Soit ABCDE un pentagone convexe, et soient M, N, P, Q, X, Y les milieux respectifs des segments BC, CD, DE, EA, MP, NQ. Montrer que (XY) est parallèle à (AB). Problème 50:Trouver toutes les polynômes P(x) et Q(x) avec des coefficient réels tel que: Q(x)=P(Q(x))\quad(\forall%20x\in\mathbb{R})) | |
|
  | |
geom
Maître
 Nombre de messages : 189 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Mer 13 Juil 2011, 11:49 Mer 13 Juil 2011, 11:49 | |
| une illustration pour le probléme 48:  | |
|
  | |
sadaso
Maître
 Nombre de messages : 92 Nombre de messages : 92
Age : 29
Date d'inscription : 23/06/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Jeu 14 Juil 2011, 18:29 Jeu 14 Juil 2011, 18:29 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Jeu 14 Juil 2011, 21:56 Jeu 14 Juil 2011, 21:56 | |
| - sadaso a écrit:
- Personne >.<
Indice pour problème 48:- Spoiler:
Sincèrement, je peux pas donner un indice pour cet exo, caar il y a beaucoup de méthodes pour le résoudre.
Indice pour problème 49:- Spoiler:
Utilise les vecteurs + Chasles pour écrire vec{XY} en fonction de vec{AB}
Indice pour problème 50:- Spoiler:
Disjonction de cas: P(x) est constante ou P(x) n'est pas constante puis travailler sur le degré de P(x) et Q(x).
remarquer que deg(P(x).Q(x))=deg(P(x))+deg(Q(x)) et deg(P(Q(x)))=deg(P(x)).deg(Q(x))
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 15 Juil 2011, 11:26 Ven 15 Juil 2011, 11:26 | |
| Plus de 48 heures sont passées, tu dois poster tes réponses ali-mes  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 15 Juil 2011, 14:25 Ven 15 Juil 2011, 14:25 | |
| - Azerty1995 a écrit:
- Plus de 48 heures sont passées, tu dois poster tes réponses ali-mes
 A 5 heures ! inxaalah | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 15 Juil 2011, 21:01 Ven 15 Juil 2011, 21:01 | |
| Désolé pour le retard, je viens de me connecter. je commence par proposer une réponse pour problème 50, les autres après car je dois refaire la démonstration. Ma réponse pour problème 50:- Spoiler:
Soit P(x) et Q(x) deux polynômes vérifiant: P(x)Q(x)=P(Q(x)) (*) pour tous réel x. Comme j'ai déjà mentionné, on va faire une disjonction de cas: * Si P(x) est constante, alors il existe un réel c tel que: P(x)=c. On remplace dans (*) et on trouve: c.Q(x)=c <=> c.Q(x)-c=0 <=> c(Q(x)-1)=0 <=> c=0 ou Q(x)=1* Si P(x) n'est pas constante, donc deg(P(x))>0 et deg(Q(x))>0 On a P(x)Q(x)=P(Q(x))=>deg(P(x)Q(x))=deg(P(Q(x))) => deg(P(x))+deg(Q(x))=deg(P(x)).deg(Q(x)) Pour simplifier, posons deg(P(x))=X et deg(Q(x))=Y. On a donc X+Y=XY (avec X et Y des entiers strictement positifs) On résous d'abord dans  l'équation: X+Y=XY <=> XY-Y=X <=> Y(X-1)=X (X est différent de 1, car si X=1 on aura 0=1 contradiction) <=>  On a:  \in%20\left%20\{%20(0,0)/(2,2)%20\right%20\}) X et Y sont deux entiers strictement positifs donc X=2 et Y=2 <=> deg(P(x))=2 et deg(Q(x))=2 deg(P(x))=2 <=> P(x)=ax²+bx+c (avec a difféent de zéro) deg(P(x))=2 <=> P(x)=dx²+ex+f (avec d difféent de zéro) En remplaçant dans (*) on trouve: (ax²+bx+c)(dx²+ex+f)=a(dx²+ex+f)²+b(dx²+ex+f)+c <=>adx^4+aex^3+afx²+bdx^3+bex²+bfx+cdx²+cex+cf=a(d²x^4+e²x²+f²+2dex^3+2dfx²+2efx)+bdx²+bex+bf+c <=>adx^4+aex^3+afx²+bdx^3+bex²+bfx+cdx²+cex+cf=ad²x^4+ae²x²+af²+2adex^3+2adfx²+2aefx+bdx²+bex+bf+c <=> (ad-ad²)x^4+(ae+bd-2aed)x^3+(af+be+cd-ae²-2adf-bd)x²+(bf+ce-2aef-be)x+(cf-af²-bf-c)=0  Après beaucoup de calculs moches, on trouve (à part les autres cas déjà traités): a un réel quelconque différent de zéro et b=c=e=f=0 et d=1 Synthèse: Les polynômes qui satisfont le problème sont: * P(x)=0 et Q(x) est un polynôme quelconque.
* P(x) est un polynôme constant quelconque et Q(x)=1
* P(x)=ax² et Q(x)=x² (avec a un réel différent de 0)
CQFD
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 15 Juil 2011, 21:51 Ven 15 Juil 2011, 21:51 | |
| Ma réponse pour problème 49: (Niveau 2AC) - Spoiler:
Propriété utilisée: Soit ABC un triangle, et soient I et J les mileux de [AB] et [AC]. On a  . Démonstration: d'après Chasles:  . Passons à notre exo:  D'après chasles et la propriété déjà démontrée on a: \\%20\overrightarrow{BA}=2(\overrightarrow{MX}+\overrightarrow{XY}+\overrightarrow{YN}+\overrightarrow{PX}+\overrightarrow{XY}+\overrightarrow{YQ})\\%20\end{matrix}) X le milieu de [MP]  Y le milieu de [QN]  On conclut que: =4\overrightarrow{XY}\Rightarrow%20(XY)//(AB)) . CQFD.
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 15 Juil 2011, 22:20 Ven 15 Juil 2011, 22:20 | |
| Si Dieu veut, je vais poster ma réponse après pour problème 48, car je suis vraiment intéressé par voir les différentes réponses pour ce joli exo. Ne l'abadonnez pas, car il est vraiment intéressant. Dans ce temps, je propose deux autres exos: Problème 51: (*) Considérons l'ensemble E={5,55,105,155,...,1955,2005} Et A une partie de E ne contenant pas deux nombres dont la somme est égale à 2010. Démontrer que Card(A) 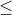 21. problème 52:On considère n points du plan (n>4). Démontrer que l'on peut relier ces points par des flèches de telle sorte que de chaque point à n'importe quel autre point en suivant une ou deux flèches.
Dernière édition par ali-mes le Mar 19 Juil 2011, 18:36, édité 1 fois | |
|
  | |
geom
Maître
 Nombre de messages : 189 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 15 Juil 2011, 22:53 Ven 15 Juil 2011, 22:53 | |
| | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 16 Juil 2011, 12:52 Sam 16 Juil 2011, 12:52 | |
| Voici la reponse du problème 48 que je vous propose,elle est en retard mais la voici - Spoiler:
On va prouver que MX=MY=MZ
Soit I le milieu de [BC]
Soit E un points tel que M est le milieu de [YE]
Soit F un points tel que M est le milieu de [ZF]
Et enfin considérons G le point d'intersection de (FY) et le cercle (C) conscrit du triangle ABC
Puisque Y£(C) Donc BYC est un triangle rectangle en Y
Donc (YC) et (BY) sont perpendiculaires
Ainsi (YC) et (PX) sont paralléles
Puisque M est le milieu des segment AC et YE
donc E£(PX) donc (EX) et (XY) sont perpendiculaires
Ainsi le triangle EXY est rectangle en X
et puisque M est le milieu de [YE] donc MX=MY=ME
D'ou MX=MY
On a Z£(C) Donc angle{BZC}=angle{BZI}+ angle{IZC}=90°
Puisque G et B etC et Z Appartiennent à (C)
Donc angle{GBC}=angle{GZC}
I est le milieu du segment BC donc I est le centre du cercle (C)
Ainsi BI=IZ D'ou angle{IBZ}=angle{IZB}
On conclut que angle{ZBG}= angle{IBZ} +angle{GBC}=angle{IZB}+ angle{GZC}=90°
DONC [ZG] est un diamètre dans le cercle (C)
D'ou YZG est un triangle rectangle en Y
Ainsi
FYZ est un triangle rectangle en Y
et puisque M est le milieu de [ZF]
Donc MZ=MY=MF
Ainsi MZ=MY
Enfin on concult queMZ=MY=MX
| |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 16 Juil 2011, 15:32 Sam 16 Juil 2011, 15:32 | |
| Problème 51: (*) :
je croix que card(A) <= 21 par 22 . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 16 Juil 2011, 17:20 Sam 16 Juil 2011, 17:20 | |
| - upsilon a écrit:
- Voici la reponse du problème 48 que je vous propose,elle est en retard mais la voici
- Spoiler:
On va prouver que MX=MY=MZ
Soit I le milieu de [BC]
Soit E un points tel que M est le milieu de [YE]
Soit F un points tel que M est le milieu de [ZF]
Et enfin considérons G le point d'intersection de (FY) et le cercle (C) conscrit du triangle ABC
Puisque Y£(C) Donc BYC est un triangle rectangle en Y
Donc (YC) et (BY) sont perpendiculaires
Ainsi (YC) et (PX) sont paralléles
Puisque M est le milieu des segment AC et YE
donc E£(PX) donc (EX) et (XY) sont perpendiculaires
Ainsi le triangle EXY est rectangle en X
et puisque M est le milieu de [YE] donc MX=MY=ME
D'ou MX=MY
On a Z£(C) Donc angle{BZC}=angle{BZI}+ angle{IZC}=90°
Puisque G et B etC et Z Appartiennent à (C)
Donc angle{GBC}=angle{GZC}
I est le milieu du segment BC donc I est le centre du cercle (C)
Ainsi BI=IZ D'ou angle{IBZ}=angle{IZB}
On conclut que angle{ZBG}= angle{IBZ} +angle{GBC}=angle{IZB}+ angle{GZC}=90°
DONC [ZG] est un diamètre dans le cercle (C)
D'ou YZG est un triangle rectangle en Y
Ainsi
FYZ est un triangle rectangle en Y
et puisque M est le milieu de [ZF]
Donc MZ=MY=MF
Ainsi MZ=MY
Enfin on concult queMZ=MY=MX
J'ai lis votre preuve, elle est juste, je vous félicite. Tu peux proposer un autre exo si tu veux. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 16 Juil 2011, 17:28 Sam 16 Juil 2011, 17:28 | |
| - az360 a écrit:
- Problème 51: (*) :
je croix que card(A) <= 21 par 22 . Non, c'est 22. Voilà la version originale (tiré d'un ancien olymp de TSM):  | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Dim 17 Juil 2011, 12:02 Dim 17 Juil 2011, 12:02 | |
| Solution au probleme 50:
Nomons m le degre du polynome P(x) et n le degré du polynome Q(x) tel que m et n appartiennent a IN.
On a alors mn=m+n
ainsi (m-1)(n-1)=1
alors (m=2 et n=2) ou (m=0 et n=0)
alors P(x)=ax²+bx+c (a=/=0) et Q(x)=a'x²+b'x+c' (a'=/=0)
ou P(x)=Q(x)=0
sauf erreur. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Dim 17 Juil 2011, 13:14 Dim 17 Juil 2011, 13:14 | |
| - yasserito a écrit:
- Solution au probleme 50:
Nomons m le degre du polynome P(x) et n le degré du polynome Q(x) tel que m et n appartiennent a IN.
On a alors mn=m+n
ainsi (m-1)(n-1)=1
alors (m=2 et n=2) ou (m=0 et n=0)
alors P(x)=ax²+bx+c (a=/=0) et Q(x)=a'x²+b'x+c' (a'=/=0)
ou P(x)=Q(x)=0
sauf erreur. je pense pas, dans votre preuve deux polynômes quelconques dont le degré est égal à 2 satistfont la condition de l'exo, prends p(x)=x²+2 et Q(x)=x²+2 Donc P(x)Q(x)=(x²+2)² et P(Q(x))=(x²+2)²+2 d'où (x²+2)²=(x²+2)²+2 donc 0=2 contradiction. En plus, deg(P(x))=0 implique P(x)=cte (un réel quelconque et pas nécessairement 0 comme tu as fait). J'ai déjà proposé une réponse pour ce problème (qui est en effet d'un ancien olympiade de 1ere), tu vas trouver la réponse juste. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Dim 17 Juil 2011, 14:07 Dim 17 Juil 2011, 14:07 | |
| | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Mar 19 Juil 2011, 12:28 Mar 19 Juil 2011, 12:28 | |
| - ali-mes a écrit:
- az360 a écrit:
- Problème 51: (*) :
je croix que card(A) <= 21 par 22 .
Non, c'est 22.
Voilà la version originale (tiré d'un ancien olymp de TSM):
 Ali , tu peut me donner un exemple ou il y'a 22 elements dans A qui satisfait l’énonce ? merci ^^ . | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Mar 19 Juil 2011, 18:35 Mar 19 Juil 2011, 18:35 | |
| - az360 a écrit:
- ali-mes a écrit:
- az360 a écrit:
- Problème 51: (*) :
je croix que card(A) <= 21 par 22 .
Non, c'est 22.
Voilà la version originale (tiré d'un ancien olymp de TSM):
 Ali , tu peut me donner un exemple ou il y'a 22 elements dans A qui satisfait l’énonce ? merci ^^ . Désolé, vous avez raison, l'inégalité est plutôt stricte. C'est ma faute parceque j'ai cru que CardE=43 et c'est plutôt CardE=41. (Je dois revoir le vidéo de AoPS: introduction to counting 2  ). Donc, l'énoncé de l'exo original est faux (chose normal dans les olympiades marocaines). Encore une fois, excusez moi. je vais éditer l'énoncé que j'ai proposé au début. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Mar 19 Juil 2011, 19:42 Mar 19 Juil 2011, 19:42 | |
| | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Mar 19 Juil 2011, 23:10 Mar 19 Juil 2011, 23:10 | |
| Solution au problème 51- Spoiler:
Partageons l'ensemble E en deux sous-ensemble I et J tel qu'à tout élément j de J, on peut associer un élément i de I / i+j=2010.
Soit k un entier naturel / 0<=k<=20
Posons I={5+50k} et J={2005-50k}
Ainsi I={5;55;...;955;1005} et J={1005;1055;...;2005}
On a bien I U J= E et pour tout élément j=2005-50k de J, il existe un élément i=5+50k de I tel que i+j=2010 (Puisque i+j=5+50k+2005-50k=2010)
De plus Card(I)=Card(J)=21
La conclusion s'en suit en appliquant le principe des tiroirs (en choisissant comme tiroirs I et J)!
Et je n'ai pas de problèmes à proposer!
| |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  | |
| |
|
  | |
| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
