| | Limiiite Arctan !!!!! |  |
|
|
| Auteur | Message |
|---|
medtaha
Féru
 Nombre de messages : 32
Age : 29
Localisation : Casablanca
Date d'inscription : 30/10/2010
| | Sujet: Limiiite Arctan !!!!! Jeu 01 Déc 2011, 12:15 | |
| [url=<script src='http://img10.imageshack.us/shareable/?i=limt.png&p=tl' type='text/javascript'></script><noscript>  </noscript>]<script src='http://img10.imageshack.us/shareable/?i=limt.png&p=tl' type='text/javascript'></script><noscript> </noscript>[/url] | |
|
| | |
manazerty
Maître
 Nombre de messages : 123
Date d'inscription : 29/06/2011
| | Sujet: Re: Limiiite Arctan !!!!! Jeu 01 Déc 2011, 12:39 | |
| lim =2
utilise le fait que pour tout x>0 : 0<(x-arctx)/x² <x/3 | |
|
| | |
medtaha
Féru
Nombre de messages : 32
Age : 29
Localisation : Casablanca
Date d'inscription : 30/10/2010
| | Sujet: Re: Limiiite Arctan !!!!! Jeu 01 Déc 2011, 12:57 | |
| wé je sais cette inegalite mais je sais po comment l'user ??,!!! | |
|
| | |
manazerty
Maître
Nombre de messages : 123
Date d'inscription : 29/06/2011
| | Sujet: Re: Limiiite Arctan !!!!! Jeu 01 Déc 2011, 13:30 | |
| remplaces x par 1/x dans l'inégalité -x/3<(x-arctx)/x² <0 c-a-d dans -x^3/3<arctgx -x <0 afin qu'elle soit utilisée pour les x négatifs..après , essayes de mettre -(x-1)².artg(1/x) +x entre deux expressions dont la lim est de 2 | |
|
| | |
ipek
Habitué
Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
| | Sujet: Re: Limiiite Arctan !!!!! Mer 08 Oct 2014, 17:28 | |
| non la lim c'est 0 j pense! | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| |
| | |
ipek
Habitué
Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
| | Sujet: Re: Limiiite Arctan !!!!! Mer 08 Oct 2014, 19:09 | |
| nmo lim je pense est :
lim (arctanx_x)/x²
x=>0 | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Limiiite Arctan !!!!! Jeu 09 Oct 2014, 11:52 | |
| - ipek a écrit:
- nmo lim je pense est :
lim (arctanx_x)/x²
x=>0 Si c'est la cas, on pose ) . Alors, on est amené à calculer }) . Il est facile de voir que les deux fonctions -x-\frac{x^3}{3}) et -x) sont positives sur ] 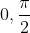 [. Et on aura, en combinant ces résultats, que }{\tan^2(t)}\le-\frac{t^3}{3\tan^2(t)}) et ainsi }{\tan^2(t)}\le0) . Ces mêmes fonctions sont négatives sur ] 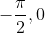 [. Et on aura de même que }\le\frac{t-\tan(t)}{\tan^2(t)}) et ainsi }{\tan^2(t)}) . Or, s'agissant d'une fonction continue, on a }{\tan^2(t)}=\lim_{t\to0+}\frac{t-\tan(t)}{\tan^2(t)}=\lim_{t\to0-}\frac{t-\tan(t)}{\tan^2(t)}) . D'après ce qui précède, on aura }=0) . Sauf erreurs. | |
|
| | |
ipek
Habitué
Nombre de messages : 26
Age : 27
Date d'inscription : 01/01/2014
| | Sujet: Re: Limiiite Arctan !!!!! Jeu 09 Oct 2014, 13:31 | |
| j ai pas compris pourquoi tu as besoin de la deuxième fonction ! | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Limiiite Arctan !!!!! Sam 11 Oct 2014, 08:55 | |
| - ipek a écrit:
- j ai pas compris pourquoi tu as besoin de la deuxième fonction !
La positivité de la deuxième fonction sur ] 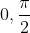[ assure la positivité de la dérive de la première fonction sur ] [. | |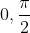
|
| | |
Contenu sponsorisé
| | Sujet: Re: Limiiite Arctan !!!!! | |
| |
|
| | |
| | Limiiite Arctan !!!!! | |
|
