| | direction mp mp* |  |
|
+11MohE Saiichi aissa expert_run kalm seledeur tahasinbad abdelbaki.attioui Mehdi.O nmo galillee56 15 participants |
|
| Auteur | Message |
|---|
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: direction mp mp* Sujet: direction mp mp*  Lun 08 Juil 2013, 16:19 Lun 08 Juil 2013, 16:19 | |
| ce topic s'adresse essentiellement a la preparation des concours de 2em annee prepa mais pas seulement tout personne interresse est la bienvenue commencant par cette exo; exo 1 soit  1-calculer det(M) 2-calculer det(M) si M appartient a Mp(Z/pZ) avec p premier. Bonne chance | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 08 Juil 2013, 18:19 Lun 08 Juil 2013, 18:19 | |
| - galillee56 a écrit:
- ce topic s'adresse essentiellement a la preparation des concours de 2em annee prepa mais pas seulement tout personne interresse est la bienvenue commencant par cette exo;
exo 1
soit 
1-calculer det(M)
2-calculer det(M) si M appartient a Mp(Z/pZ) avec p premier.
Bonne chance 1-Pour la première question:Je me souviens bien qu'on a fait lors d'un TD, le cas de n=2. Voici ma proposition pour la généralisation: Soit 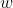 la racine (n+1)-ième de l'unité. Soit la matrice définie par:  . On a  . Je ne peux pas remplir trop de cases, car cela est difficile. On peut simplifier la première colonne, on définit le polynôme =a_0.x^{n+1}+a_1.x^n+\cdots+a_n.x) . Dans la première ligne, il y a le nombre ) . Dans la deuxième ligne, il y a le nombre ) . Et ainsi de suite... Même chose pour ce qui est des autres colonne: pour la j-ième colonne: on définit le polynôme =a_0.x^{n+1}+\cdots+a_n.x) . Dans la j-ième ligne, il y a le nombre ) . Et ainsi de suite... D'où, on arrive à peine à avoir une chose du genre:  & \omega.P_2(\omega)& \omega^2.P_3(\omega) & \cdots & \omega^{n-1}.P_{n}(\omega)&\omega^n.P_{n+1}(\omega) \\ \omega^n.P_1(\omega) & P_2(\omega) & \omega.P_3(\omega)&\cdots &\omega^{n-2}.P_n(w) &\omega^{n-1}.P_{n+1}(\omega) \\ \omega^{n-1}.P_1(\omega) & \omega^{n}.P_2(\omega) & P_3(\omega) & \cdots & \cdots & \cdots\\ \cdots &\omega^{n-1}.P_2(\omega) & \cdots & P_4(\omega) & \cdots & \cdots \\ \cdots &\cdots &\cdots &\cdots & P_{n-1}(\omega) &\cdots \\ \omega.P_1(\omega) &\omega^2.P_2(\omega) &\cdots & \cdots &\omega^{n-1}.P_{n-1}(\omega) & P_{n+1}(\omega)\end{pmatrix}) . Et ainsi: =\begin{vmatrix}P_1(\omega) & \omega.P_2(\omega)& \omega^2.P_3(\omega) & \cdots & \omega^{n-1}.P_{n}(\omega)&\omega^n.P_{n+1}(\omega) \\ \omega^n.P_1(\omega) & P_2(\omega) & \omega.P_3(\omega)&\cdots &\omega^{n-2}.P_n(w) &\omega^{n-1}.P_{n+1}(\omega) \\ \omega^{n-1}.P_1(\omega) & \omega^{n}.P_2(\omega) & P_3(\omega) & \cdots & \cdots & \cdots\\ \cdots &\omega^{n-1}.P_2(\omega) & \cdots & P_4(\omega) & \cdots & \cdots \\ \cdots &\cdots &\cdots &\cdots & P_{n-1}(\omega) &\cdots \\ \omega.P_1(\omega) &\omega^2.P_2(\omega) &\cdots & \cdots &\omega^{n-1}.P_{n-1}(\omega) & P_{n+1}(\omega)\end{vmatrix}) . Donc: =\prod_{i=1}^{n+1}P_i(\omega)\begin{vmatrix}1& \omega & \omega^2 & \cdots & \omega^{n-1}&\omega^n \\ \omega^n & 1 & \omega &\cdots &\omega^{n-2} &\omega^{n-1} \\ \omega^{n-1} & \omega^{n} & 1 & \cdots & \cdots & \cdots\\ \cdots &\omega^{n-1} & \cdots & 1 & \cdots & \cdots \\ \cdots &\cdots &\cdots &\cdots & 1 &\cdots \\ \omega &\omega^2 &\cdots & \cdots &\omega^{n-1} & 1\end{vmatrix}=\prod_{i=1}^{n+1}P_i(\omega).\det(X_{n+1})) . On conclût donc que: =\prod_{i=1}^{n+1}P_i(\omega)) . C'est ça l'idée, mais je vois que c'est difficile de manipuler le résultat. Si quelqu'un aura une autre solution, elle sera la bienvenue. 2-Pour la deuxième question: Je ne sais pas ce qui est demandé car je ne sais pas ce que la notation veut dire. Merci d'éclaircir... Remarque:Cette solution est fausse, même j'ai fournit un large effort de rédaction... Pour plus d'information, voir ici: https://fr.wikipedia.org/wiki/Matrice_circulante.
Dernière édition par nmo le Lun 08 Juil 2013, 22:42, édité 2 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 08 Juil 2013, 18:41 Lun 08 Juil 2013, 18:41 | |
| bien joue mr.nmo pour la 2em ca veut dire que mes a_i sont dans Z/pZ je garde les meme propriete et surtout a^p=a en gros je reduis modulo p  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 08 Juil 2013, 19:27 Lun 08 Juil 2013, 19:27 | |
| - galillee56 a écrit:
- bien joue mr.nmo
pour la 2em ca veut dire que mes a_i sont dans Z/pZ je garde les meme propriete et surtout a^p=a en gros je reduis modulo p  Merci pour la réponse. Je viens de constater que les polynômes que j'ai défini sont égaux, je les nomme P. Le déterminant devient donc =P(\omega)^{n+1}=(a_0+a_1.\omega^{n}+\cdots+a_n.\omega)^{n+1}) . Donc, dans la deuxième question, on est amené à calculer le produit: =(a_0+a_1.\omega^{p-1}+\cdots+a_{p-1}.\omega)^{p}) sous les contraintes imposées, et en tenant compte que 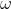 est une racine p-ième de l'unité. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 08 Juil 2013, 20:13 Lun 08 Juil 2013, 20:13 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 08 Juil 2013, 21:57 Lun 08 Juil 2013, 21:57 | |
| Proposez un autre exerice, je crois que celui-là n'est pas intéressant ( juste calculatoire )  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 08 Juil 2013, 22:36 Lun 08 Juil 2013, 22:36 | |
| - Mehdi.O a écrit:
- Proposez un autre exerice, je crois que celui-là n'est pas intéressant ( juste calculatoire )
 Je partage ton avis, je change donc de terrain vers l'analyse: Exercice 2:Soit 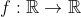 une fonction définie par: : f(\alpha)=\int_{0}^{+\infty}\frac{\ln(y)}{e^{\alpha.y}+1}dy) . Sachant que  s'annule au point  et que 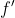 s'annule au point 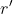 , calculez l'intégrale: d\alpha) . Bonne chance. | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 10:34 Mar 09 Juil 2013, 10:34 | |
| pour tout x de R, ln(y)/(exp(xy)+1)~ln(y)/2 quand y-->0+ comme y-->ln(y) est intégrable sur ]0,1] alors y-->ln(y)/(exp(xy)+1) est intégrable sur ]0,+00[ ssi y-->ln(y)/(exp(xy)+1) est intégrable sur [1,+00[. Noter qu'il y a équivalence entre intégrabilité et convergence de l'intégrale ( la fonction garde un signe constant)
ln(y)/(exp(xy)+1)~ln(y)exp(-xy) quand y-->+00 donc l'intégrale sur [1,+00[ converge ssi x>0
donc le domaine de f est ]0,+00[ ==> r et r'>0
soit x>0, on pose z=xy
f(x)
=int( 0,+00) ln(y)/(exp(xy)+1) dy
= 1/x. int( 0,+00) ( ln(z)-ln(x))/(exp(z)+1) dz
=( f(1)-a.ln(x))/x où a= int( 0,+00) 1/(exp(z)+1) dz
on pose t=exp(z) ==> dt=t dz
a=int( 1,+00) 1/t(t+1) dt = int( 1,+00) (1/t-1/(t+1)) dt=ln(2)
donc f(x)= f(1)/x -ln(2).ln(x)/x et f'(x)= -f(1)/x² -ln(2)( 1-ln(x))/x²
f(r)=0 <==> f(1)=ln(2).ln(r)
f'(r')=0 <==> f(1)=-ln(2).(1-ln(r')) donc ln(r)=ln(r')-1
int( r , r') f(x)dx
= f(1) (ln(r')-ln(r))-ln(2)( ln(r')²-ln(r)²)/2
= f(1) -ln(2). ( ln(r')+ln(r))/2
=ln(2)ln(r)-ln(2)(2ln(r)+1)/2
=-ln(2)/2
Dernière édition par abdelbaki.attioui le Mar 09 Juil 2013, 17:08, édité 1 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 10:50 Mar 09 Juil 2013, 10:50 | |
| - abdelbaki.attioui a écrit:
- pour tout x de R, ln(y)/(exp(xy)+1)~ln(y)/2 quand y-->0+ comme y-->ln(y) est intégrable sur ]0,1] alors y-->ln(y)/(exp(xy)+1) est intégrable sur ]0,+00[ ssi y-->ln(y)/(exp(xy)+1) est intégrable sur [1,+00[. Noter qu'il y a équivalence entre intégrabilité et convergence de l'intégrale ( la fonction garde un signe constant)
ln(y)/(exp(xy)+1)~ln(y)exp(-xy) quand y-->+00 donc l'intégrale sur [1,+00[ converge ssi x>0
donc le domaine de f est ]0,+00[ ==> r et r'>0
soit x>0, on pose z=xy
f(x)
=int( 0,+00) ln(y)/(exp(xy)+1) dy
= 1/x. int( 0,+00) ( ln(z)-ln(x))/(exp(z)+1) dz
=( f(1)-a.ln(x))/x où a= int( 0,+00) 1/(exp(z)+1) dz
on pose t=exp(z) ==> dt=t dz
a=int( 1,+00) 1/t(t+1) dt = int( 1,+00) (1/t-1/(t+1)) dt=ln(2)
donc f(x)= f(1)/x -ln(2).ln(x)/x et f'(x)= -f(1)/x² -ln(2)( 1-ln(x))/x²
f(r)=0 <==> f(1)=ln(2).ln(r)
f'(r')=0 <==> f(1)=-ln(2).(1-ln(r')) donc ln(r)=ln(r')-1
int( r , r') f(x)dx
= f(1) (ln(r')-ln(r))-ln(2)( ln(r')²-ln(r)²)/2
= f(1) -ln(2). ( ln(r')+ln(r))/2
=ln(2)ln(r)-ln(2)(2ln(r)-1)/2
=ln(2)/2 Wow, merci pour votre methode mr attioui j'etais partie sur un methode de bourrin qui a aboutit a la fin mais apres plusieur page de calcul Merci. Restons en analyse Exo3:trouver la limite de la suite  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 13:12 Mar 09 Juil 2013, 13:12 | |
| - abdelbaki.attioui a écrit:
- int( r , r') f(x)dx
= f(1) (ln(r')-ln(r))-ln(2)( ln(r')²-ln(r)²)/2
= f(1) -ln(2). ( ln(r')+ln(r))/2
=ln(2)ln(r)-ln(2)(2ln(r)-1)/2
=ln(2)/2 Très bien joué! Il y a une petite faut d'inattention dans ce qui est en rouge. Le bon résultat est l'opposé de ce que tu as trouvé. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 14:14 Mar 09 Juil 2013, 14:14 | |
| Solution de l'exercice 3 :Tout d'abord , on remarque que :  . Maintenant, on démontre le lemme suivant : Lemme :Soit f une fonction de classe C^3 sur [0,1], on a :  Preuve: Preuve:Soit 0<=k<=n-1, on applique le théorème de Taylor-Lagrange sur f entre t et k/n, on obtient :  , d'où en posant M=sup([0,1]) |f"|, on obtient :  . En sommant on obtient le résultat voulu . Maintenant ,en revenant au problème , on obtient compte tenu de la convergence des sommes de Riemman :  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 14:26 Mar 09 Juil 2013, 14:26 | |
| bien joue Mehdi.O a vous de proposer un exo  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 14:44 Mar 09 Juil 2013, 14:44 | |
| Passons un peu aux polynômes: Exercice 4:Soit 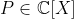 , trouver une condition nécessaire et suffisante sur P pour que celui induise une surjection de Q sur Q. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 16:35 Mar 09 Juil 2013, 16:35 | |
| il est evident que les degres 1 verifient et les constantes ne verifie pas soit n=deg(P) supposons que n>2  , 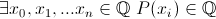 ,  ,  ,  en multipliant par une constante pres on peut supposer 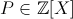 ,  ,  ,  ,  CQFD CQFD | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 16:41 Mar 09 Juil 2013, 16:41 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 16:49 Mar 09 Juil 2013, 16:49 | |
| voici un exo assez facile classique mais que j'aime bien trouver A dans Mn(R) tel que pour tout B dans Mn(R) det(A+B)=det(A)+det(B) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 16:58 Mar 09 Juil 2013, 16:58 | |
| - galillee56 a écrit:
- voici un exo assez facile classique mais que j'aime bien trouver A dans Mn(R) tel que pour tout B dans Mn(R) det(A+B)=det(A)+det(B)
Euh y a sûrement une erreur, pour A=0  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 17:02 Mar 09 Juil 2013, 17:02 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 17:07 Mar 09 Juil 2013, 17:07 | |
| - galillee56 a écrit:
- euuh seul A=0 verifie
Tu as dit trouver A, bon je t'invite à reforumuler l'exercice et à le numéroter aussi. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 17:10 Mar 09 Juil 2013, 17:10 | |
| Exo5:
Trouver toute les matrices A dans Mn(R) tq pour tout B dans Mn(R) det(A+B)=det(A)+det(B)
Dernière édition par galillee56 le Mar 09 Juil 2013, 17:11, édité 1 fois | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 17:10 Mar 09 Juil 2013, 17:10 | |
| - nmo a écrit:
- abdelbaki.attioui a écrit:
- int( r , r') f(x)dx
= f(1) (ln(r')-ln(r))-ln(2)( ln(r')²-ln(r)²)/2
= f(1) -ln(2). ( ln(r')+ln(r))/2
=ln(2)ln(r)-ln(2)(2ln(r)-1)/2
=ln(2)/2 Très bien joué!
Il y a une petite faut d'inattention dans ce qui est en rouge.
Le bon résultat est l'opposé de ce que tu as trouvé.
effectivement, c'est rectifié et merci nmo | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 17:13 Mar 09 Juil 2013, 17:13 | |
| - Mehdi.O a écrit:
- galillee56 a écrit:
- euuh seul A=0 verifie
Tu as dit trouver A, bon je t'invite à reforumuler l'exercice et à le numéroter aussi. Merci Mehdi.O  | |
|
  | |
tahasinbad
Maître
 Nombre de messages : 158 Nombre de messages : 158
Age : 30
Date d'inscription : 02/12/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 18:11 Mar 09 Juil 2013, 18:11 | |
| Pour ton exo ghali :
Je propose cette solution
Soit A une matrice qui verifie les coditions donnees et soit r son rang donc il existe Q et P tq A =Q.Jr.P
Prenons pour B la mateice Q(In-Jr)P , on a alors det(P).det(Q)=det(A +B) =det(P).det(Q).det(Jr) +
Det(Q).det(P).det(In-Jr)
Ainsi det(Jr) + det (In-Jr) = 1
Donc soit r =0 soit 1
Pour r=1 on peut donner une contradiction en prenant B=A=In.
Donc A=0. Je mettrais mn exo apres. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 18:14 Mar 09 Juil 2013, 18:14 | |
| bien joue  | |
|
  | |
tahasinbad
Maître
 Nombre de messages : 158 Nombre de messages : 158
Age : 30
Date d'inscription : 02/12/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 09 Juil 2013, 18:29 Mar 09 Juil 2013, 18:29 | |
| Voila un exercice d'analyse :
Soit une fonction f : R -> R telle que pour tout segment [a,b] de R , f([a,b]) est un segment et telle que f^(-1) ({x}) est ferme pour tt x appartenant a R . Montrer que f est continue. ( c'est classique ) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  | |
| |
|
  | |
| | direction mp mp* |  |
|
