| | direction mp mp* |  |
|
+11MohE Saiichi aissa expert_run kalm seledeur tahasinbad abdelbaki.attioui Mehdi.O nmo galillee56 15 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 12:54 Mer 10 Juil 2013, 12:54 | |
| - galillee56 a écrit:
- voici ce que je propose
- Spoiler:
grace a un binome de Newton on prouve que:  ,  , 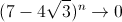 , 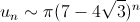 donc la serie de terme general u_n converge
Excellent! Je propose un autre exercice: Exercice 10:Soient  des fonctions continues. On suppose que  pour tous les (a,b) réels. Prouvez que: : f_k=0) . Bonne chance. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 13:09 Mer 10 Juil 2013, 13:09 | |
| supponsons que tout les sont non identiquement nul soit x_i la premiere fois ou f_i sur [0,1] (si elle s annulle) soit x_m= min( x_i) a=0 b=x_m le produit different de 0 impossible donc il existe k tel que f_k=0 | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 13:12 Mer 10 Juil 2013, 13:12 | |
| ps: elle pourrait coincider ac la fonction nul en [0,1] mais d'apres mon hypothese il existe bien un intervalle ou elle ne coincide pas ac la fonction nul donc je gagne et pour le x_i je ne le compte que je change de signe | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 13:27 Mer 10 Juil 2013, 13:27 | |
| - galillee56 a écrit:
- ps: elle pourrait coincider ac la fonction nul en [0,1] mais d'apres mon hypothese il existe bien un intervalle ou elle ne coincide pas ac la fonction nul donc je gagne et pour le x_i je ne le compte que je change de signe
Désolé, mais ton raisonnement est faux, déjà pour prouver que f_k=0, si le min des x_i est égal à 0 , càd s'il existe une f_i qui s'annule en 0, tu peux rien en déduire, et puis quand tu montres l'existence d'une fonction nulle dans [0,1], tu peux rien déduire pour IR .. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 14:21 Mer 10 Juil 2013, 14:21 | |
| - nmo a écrit:
- Je propose un autre exercice:
Exercice 10:
Soient  des fonctions continues. des fonctions continues.
On suppose que  pour tous les (a,b) réels. pour tous les (a,b) réels.
Prouvez que: : f_k=0) . .
Bonne chance. Cet exercice est tiré d'un livre qui ne cesse de m'enerver... Parfois, en l'occurrence en cet exercice, il demande de prouver quelque chose et lorsqu'on arrive plus et on décide de voir sa solution, surprise: il nous dit que "c'est faux" tout court et il donne un contre exemple. Bon, pour cet exercice: le résultat est vrai pour n=1 et n=2; mais il est faux à partir de n=3. Ainsi, la nouvelle question est de montrer le résultat pour n=2 et de trouver un contre exemple pour n=3. P.S: Je m'excuse de l'avoir proposer... | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 14:33 Mer 10 Juil 2013, 14:33 | |
| looooll apres la remarque de Mehdi.O montrons que ma demonstration est fausse j'ai planche sur ca j'ai trouve quand mm bizzare cette propriete mais tres interressante maintenant que vous dites que ca ne marche j ai en effet un contre exemple sur feuille mais juste en dessein mais pas d'une fonction explicite mais se fut quand mm interressant merci  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 14:39 Mer 10 Juil 2013, 14:39 | |
| Solution de "l'exerice 10" :Bon pour n=2, soit 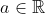 , on a pour tout x de IR :  , on dérive cette fonction et compte tenu de l'hypothèse , on obtient :  , si f_2 est non nul , on a f_2(b) non nul, donc :  , en utilisant la relation de Chasles pr deux points différents a_1 et a_2, on obtient l'intégrale de f_1 est nulle sur tout segment, donc f_1=0. Pour le contre-exemple je suis encore en train de chercher :p. J'avais prouvé le cas n=2 juste pour avoir une idée sur le cas général, smais après plusieurs tentatives j'ai pas réussi, et maintenant je suis choqué par le fait que cet exercice est faux  | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 14:45 Mer 10 Juil 2013, 14:45 | |
| Bonjour.
Je vous propose cet exercice qui me semble très intéressant .
EXO 11 :
Déterminer les entiers n de N* tels que GLn(R) contienne un sous-groupe isomorphe à Z ⁄4Z × Z ⁄4Z . | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 10 Juil 2013, 15:46 Mer 10 Juil 2013, 15:46 | |
| - Mehdi.O a écrit:
- Solution de "l'exerice 10" :
Bon pour n=2, soit 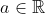 , on a pour tout x de IR : , on a pour tout x de IR :
 , on dérive cette fonction et compte tenu de l'hypothèse , on obtient : , on dérive cette fonction et compte tenu de l'hypothèse , on obtient :

,
si f_2 est non nul , on a f_2(b) non nul, donc :  , en utilisant la relation de Chasles pr deux points différents a_1 et a_2, on obtient l'intégrale de f_1 est nulle sur tout segment, donc f_1=0. , en utilisant la relation de Chasles pr deux points différents a_1 et a_2, on obtient l'intégrale de f_1 est nulle sur tout segment, donc f_1=0.
Pour le contre-exemple je suis encore en train de chercher :p.
J'avais prouvé le cas n=2 juste pour avoir une idée sur le cas général, smais après plusieurs tentatives j'ai pas réussi, et maintenant je suis choqué par le fait que cet exercice est faux  Je propose les fonctions suivantes comme contre exemple: Soit t€IR+* f_1(x)=0 sur ]-oo,t]U[2t,+oo[ et sin(2pi x/t) sur [t,2t] f_2(x)=0 sur ]-00,2t] et x-2t sur [2t;+oo[ f_3(x)=0 sur [t;+00[ et x-t sur [-oo,t] | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 10:29 Jeu 11 Juil 2013, 10:29 | |
| apparement personne n'a encore trouver l'exo 11 passant a l'exo 12 en attendant une reponse a 11
exo 12
soit f une permutation determiner la nature de la serie de terme general:
-f(n)/(n^2)
-f(n)/(n^2ln(n))
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 12:28 Jeu 11 Juil 2013, 12:28 | |
| - galillee56 a écrit:
- apparement personne n'a encore trouver l'exo 11 passant a l'exo 12 en attendant une reponse a 11
exo 12
soit f une permutation determiner la nature de la serie de terme general:
-f(n)/(n^2)
-f(n)/(n^2ln(n))
---Pour la première série: On pose: }{k^2}) . En appliquant l'inégalité de Caushy-Schwartz, on aura: ^2\le\bigg(\sum_{k=1}^{n}\frac{1}{f(k)}\bigg)\bigg(\sum_{k=1}^{n}\frac{f(k)}{k^2}\bigg)) . Or, on a: }=\sum_{k=1}^{n}\frac{1}{k}) . On déduit donc que:  . En faisant tendre n vers  , on trouve que 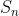 tend elle aussi vers  . Et par conséquent, la série de terme général }{n^2}) diverge. ---Pour la deuxième série: Est ce que le dénominateur est }) ou ) ? | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 12:41 Jeu 11 Juil 2013, 12:41 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 13:42 Jeu 11 Juil 2013, 13:42 | |
| - galillee56 a écrit:
- c (n^2)*(ln(n))
On pose: }{k^3}) . Il est facile d'établir que: : \ln(k)\le k) , donc : \frac{f(k)}{k^3}\le \frac{f(k)}{k^2.\ln(k)}) . Par suite, ona: : \sum_{k=1}^{n}\frac{f(k)}{k^3}\le S_n) Or, on a selon l'inégalité du réordonnement: :\sum_{k=2}^{n}\frac{n+1-k}{k^3}\le\sum_{k=2}^{n}\frac{f(k)}{k^3}) . Donc : (n+1).\sum_{k=2}^{n}\frac{1}{k^3}-\sum_{k=2}^{n}\frac{1}{k^2}\le\sum_{k=2}^{n}\frac{f(k)}{k^3}) . Ainsi, en faisant tendre n vers  on trouve que 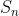 va tendre vers  . Encore une fois, la série diverge. Sauf erreurs. P.S: J'attends une confirmation. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 13:56 Jeu 11 Juil 2013, 13:56 | |
| - galillee56 a écrit:
- apparement personne n'a encore trouver l'exo 11 passant a l'exo 12 en attendant une reponse a 11
exo 12
soit f une permutation determiner la nature de la serie de terme general:
-f(n)/(n^2)
-f(n)/(n^2ln(n))
Je n'ai pas bien saisi, f est une permutation de [1,n] ?, et dans ce cas elle va dépendre de n ? | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:04 Jeu 11 Juil 2013, 14:04 | |
| - kalm a écrit:
- Bonjour.
Je vous propose cet exercice qui me semble très intéressant .
EXO 11 :
Déterminer les entiers n de N* tels que GLn(R) contienne un sous-groupe isomorphe à Z ⁄4Z × Z ⁄4Z . Indication :considérez le sous-groupe {I_2,R,R^2,R^3} de GL2(IR) ou R la matrice de rotation d'angle pi/2. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:22 Jeu 11 Juil 2013, 14:22 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:26 Jeu 11 Juil 2013, 14:26 | |
| - kalm a écrit:
- kalm a écrit:
- Bonjour.
Je vous propose cet exercice qui me semble très intéressant .
EXO 11 :
Déterminer les entiers n de N* tels que GLn(R) contienne un sous-groupe isomorphe à Z ⁄4Z × Z ⁄4Z .
Indication :considérez le sous-groupe {I_2,R,R^2,R^3} de GL2(IR) ou R la matrice de rotation d'angle pi/2. mr kalm j ai pense a ce sous groupe chose naturel puisque A^4=I donc en gros diagonalisable valeur propre (1,-1,i,-i) mais la chose qui me derange c que il etait isomorphe a Z/4Z*Z/4Z il doit etre de cardinal 16 si je ne me trompe et je n arrive pas a trouver un tel ss groupe | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:27 Jeu 11 Juil 2013, 14:27 | |
| - Mehdi.O a écrit:
- galillee56 a écrit:
- apparement personne n'a encore trouver l'exo 11 passant a l'exo 12 en attendant une reponse a 11
exo 12
soit f une permutation determiner la nature de la serie de terme general:
-f(n)/(n^2)
-f(n)/(n^2ln(n))
Je n'ai pas bien saisi, f est une permutation de [1,n] ?, et dans ce cas elle va dépendre de n ? ouii elle depend de n c une fonction qui depend de n je comprend pas votre remarque a vrai dire | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:29 Jeu 11 Juil 2013, 14:29 | |
| - galillee56 a écrit:
- Mehdi.O a écrit:
- galillee56 a écrit:
- apparement personne n'a encore trouver l'exo 11 passant a l'exo 12 en attendant une reponse a 11
exo 12
soit f une permutation determiner la nature de la serie de terme general:
-f(n)/(n^2)
-f(n)/(n^2ln(n))
Je n'ai pas bien saisi, f est une permutation de [1,n] ?, et dans ce cas elle va dépendre de n ? ouii elle depend de n c une fonction qui depend de n je comprend pas votre remarque a vrai dire Vous avez f est une permutation, ca veut une bijection de IN vers IN ? | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:34 Jeu 11 Juil 2013, 14:34 | |
| Mehdi vous avez tout a fait raison c'est une permutation de N* desole et merci pour votre remarque ramadan a 45 degre ca n aide pas merci !!  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:36 Jeu 11 Juil 2013, 14:36 | |
| - galillee56 a écrit:
- Mehdi vous avez tout a fait raison c'est une permutation de N* desole et merci pour votre remarque ramadan a 45 degre ca n aide pas merci !!
 Haha, bon déjà le terme permutation c'est pour un ensemble fini, et dans ce cas la démonstration de nmo des deux séries est fausse, car puisque c'est une bijection, ce n'est plus une permutation , il a utilisé le fait que f est une permutation de [1,n] pour tout n  , ce n'est pas possible ... | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:41 Jeu 11 Juil 2013, 14:41 | |
| je ne vois pas pk le reodennement ne marcherai plus cette serie est minimal pour l identite | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:43 Jeu 11 Juil 2013, 14:43 | |
| - galillee56 a écrit:
- je ne vois pas pk le reodennement ne marcherai plus cette serie est minimal pour l identite
L'inégalité de réordonnement s'applique juste pour une permutation. Voir http://fr.wikipedia.org/wiki/In%C3%A9galit%C3%A9_de_r%C3%A9arrangement | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:47 Jeu 11 Juil 2013, 14:47 | |
| Mais en fait, pour rectifier les deux démonstrations, il faut plutôt que d'établir des égalités, renforcer les inégalités, par exemple soit n € IN*, si l'image de [1,n] par f est [1,n] on a fini, sinon quitte à composer par une autre permutation, chaque fois que f(i) >n, on peut se ramener au cas contraire, et dans ce cas on va se ramener à la somme indiquée en haut pour l'inégalité de réordonnement, mais par une minoration  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 11 Juil 2013, 14:51 Jeu 11 Juil 2013, 14:51 | |
| c dommage qu'on puisse pas l'utiliser pour un ensemble infini surtout que dans ce cas la on le sens vraiment bien bref je m'excuse encore  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  | |
| |
|
  | |
| | direction mp mp* |  |
|
