direction mp mp*

galillee56 a écrit:

kalm a écrit:

kalm a écrit:

Bonjour.
Je vous propose cet exercice qui me semble très intéressant .
EXO 11 :
Déterminer les entiers n de N* tels que GLn(R) contienne un sous-groupe isomorphe à Z ⁄4Z × Z ⁄4Z .

Indication :considérez  le  sous-groupe {I_2,R,R^2,R^3} de GL2(IR)  ou R la matrice de rotation d'angle pi/2.

mr kalm j ai pense a ce sous groupe chose naturel puisque A^4=I donc en gros diagonalisable valeur propre (1,-1,i,-i) mais la chose qui me derange c que il etait isomorphe a Z/4Z*Z/4Z il doit etre de cardinal 16 si je ne me trompe et je n arrive pas a trouver un tel ss groupe  

Dans ce cas pour n>=4 on peut trouver un tel sous groupe non ? et vérifier les cas qui restent un par un.

kalm a écrit:

Bonjour.
Je vous propose cet exercice qui me semble très intéressant .
EXO 11 :
Déterminer les entiers n de N* tels que GLn(R) contienne un sous-groupe isomorphe à Z ⁄4Z × Z ⁄4Z .

En naviguant sur Internet, j'ai trouvé ceci:
.
Personnellement, je trouve la démonstration difficile, car on n'a pas encore étudié le chapitre de la réduction des endomorphismes et plein d'autres choses qui y figurent.
Donc, n supérieur ou égale à 2 convient, n'est ce pas?
P.S: Peut on reprendre la route vers MP et MP*?

Merci Mr nmo pour cette preuve et je crois qu'on peut continuer cette route  . Mr Kalm si vous avez une autre preuve, veuillez la partager avec nous

Voici un nouvel exercice tiré d'une épreuve de l'X:
Exercice 13:
Soit une appplication de dans vérifiant:
i) .
ii) .
iii) .
Déterminez .
Bonne chance.

nmo a écrit:

kalm a écrit:

Bonjour.
Je vous propose cet exercice qui me semble très intéressant .
EXO 11 :
Déterminer les entiers n de N* tels que GLn(R) contienne un sous-groupe isomorphe à Z ⁄4Z × Z ⁄4Z .

En naviguant sur Internet, j'ai trouvé ceci:
.
Personnellement, je trouve la démonstration difficile, car on n'a pas encore étudié le chapitre de la réduction des endomorphismes et plein d'autres choses qui y figurent.
Donc, n supérieur ou égale à 2 convient, n'est ce pas?
P.S: Peut on reprendre la route vers MP et MP*?

Le résultat ne donne malheureusement pas grand chose

Soit μ4 le groupe des 4 rotations R(k*pi⁄2) (0 ≤ k ≤ 3). C’est un sous-groupe cyclique d’ordre 4 de GL_2 (R ) donc (GL_2(R),×) contient un sous-groupe isomorphe à (Z⁄4Z,+). On en déduit que, pour n ≥ 4, GL_n(R) contient un sous-groupe isomorphe au produit cartésien Z⁄4Z × Z ⁄4Z .
∙ Supposons que GL_3(R) contienne un sous-groupe G isomorphe à Z⁄4Z × Z⁄4Z. On peut alors trouver dans GL_3(R) deux matrices A et B d’ordre 4 qui commutent et telles que {A, B} engendre G : les images des éléments (1,0) et (0,1) par un isomorphisme Z⁄4Z × Z ⁄4Z ↦→ G.
On a A^4 = I3 et A^2 ⁄= I3 donc A^2 + I3 n’est pas inversible. De ce fait i et -i sont valeurs propres de A (car elle est réelle). Par ailleurs A (de taille impaire) admet au moins une valeur propre réelle qui ne peut être que e = ±1. Ainsi A a trois valeurs propres distinctes e,i,-i et trois droites propres associées Di (i = 1,2,3).
Par ailleurs B, qui commute avec A, stabilise les trois droites propres de A. Soit μi le rapport de l’homothétie B|Di et P = a + bX + cX^2 ∈ C[X] le polynôme interpolateur de degré ≤ 2 qui envoie respectivement e,i,-i sur p1,p2,p3. On a B = P(A) = aI3 + bA + cA^2 car les endomorphismes correspondant coïncident sur les droites propres de A.
Par ailleurs, comme A et B sont réelles et I3,A,A^2 indépendantes (car le polynôme minimal de A est (X - e)(X - i)(X + i) de degré 3), les coefficients a,b,c sont aussi réels. En effet, en conjugant on a B = a'I3 + b'A + c'A^2 = aI3 + bA + cA^2 donc (a',b',c') = (a,b,c). (a'=a barre)
Or, avec les notations précédentes, on a P(e) = p1,P(i) = p2,P(-i) = p3, comme les valeurs propres de B sont aussi ± 1,i,-i, le fait que P est réel impose p1 = ±1,p2 = -p3 = ±i.
Étudions les quatre possibilités :
i) si p1 = e et p2 = i alors p3 = -i donc B = A et le groupe engendré par A et B est de cardinal 4 ;
ii) si p1 = e et p2 = -i alors p3 = i, B = A^3 et le groupe engendré par A et B est encore de cardinal 4 ;
iii) si p1 = -e et p2 = -i alors p3 = i, B = -A et le groupe engendré par A et B est aussi engendré par A et - I2 donc il est de cardinal ≤ 8 ;
iv) si p1 = -e et p2 = i alors p3 = -i, B = -A^3 et le groupe engendré par A et B est encore engendré par A et - I2 donc il est de cardinal ≤ 8.
En conclusion GL_3(R) ne contient pas de sous-groupe isomorphe à Z⁄4Z × Z⁄4Z et donc, a fortiori, GL_p (R ) n’en contient pas non plus si p ≤ 2.

BSR
pour n =2 soit r la rotation d'angle pi/2 et s la symétrie d'axe vect(i); H=<r,s> le sous groupe engendré par r et s alors H est isomorphe à Z/4ZxZ/4Z et aussi isomorphe à un sous groupe de M_2(IR)
(Groupe Diédral ;ou groupe du carré )
existe -t-il d'autre valeurs pour n?

nmo a écrit:

Voici un nouvel exercice tiré d'une épreuve de l'X:
Exercice 13:
Soit une appplication de dans vérifiant:
i) .
ii) .
iii) .
Déterminez .
Bonne chance.

Solution:
On démontre facilement que f(x)=x ; x€IQ.
Or l'équation y=x+1/x admet une solution pour tout y de IR tq |y|>=2
Fixons donc un tel y.
|f(y)|=|f(x)+(1/f(x))|>=2
et par passage à l'inverse on obtient donc que pour tout x de IR* tq |x|<=1/2 on a |f(x)|<=1/2.
Par la suite on se fixe un x dans IR et soit (a_n) une suite de rationnels tq |x-a_n|<=1/(2n)
alors  |f(nx-na_n)/n|=|f(x)-a_n|<=1/2n  d'où f(x)=x par passage à la limite .
Donc l'application identité est la seule application vérifiant les conditions de l'exercice.

je m excuse je doit dormir mon sous groupe H est isomorphe à Z/4ZxZ/2Z et non pas à Z/4ZxZ/4Z !!!
pour ex13
on montre que f(x)=x si x est dans Q
f est croissante sur Q puis sur IR on utilise la densité de Qdans IR pour conclur
rq f = id_R est la seule fonction vérifiant i) et ii)

revenons a nos moutons :
Exo 14:
soit x rationelle tel que cos(pix) soit rationnelle trouver x

galillee56 a écrit:

revenons a nos moutons :
Exo 14:
soit x rationelle tel que cos(pix) soit rationnelle trouver x

Solution
Soit x un rationnel alors il existe (p;q)€IZXIZ*  tq x=p/q
Or on sait que P_q(cos(Pix)=cos(pi*p)=(-1)^p avec P_q le q-ème polynôme de Tchebychev.
On peut alors écrire P_q de la forme 2^(q-1)x^q+Q(x) avec Q un polynôme à coefficients entiers  de degré inférieur ou égal à n-1.
Supposons que cos(pix) est rationnel non nul alors  il existe (a;b)€IZ*XIN* avec pgcd(a;b)=1 tq cos(pix)=a/b
et donc 2^(q-1)a^q+b^qQ(x)=(-1)^p*b^q alors  b/2^(q-1)*a^q  donc b=2b' ce qui donne 2b'/a^q
et par conséquent b'=1  d'ou cos(pix)=a/2  . le a ne peut prendre que -2:-1;1;2 s'ajoute à ceci le cas ou a=0 alors les valeurs possibles de cos(pix) sont {-1;-1/2;0;1/2;1}. La tache donc devient facile pour retrouver les x .

expert_run a écrit:

galillee56 a écrit:

revenons a nos moutons :
Exo 14:
soit x rationelle tel que cos(pix) soit rationnelle trouver x

Solution
Soit x un rationnel alors il existe (p;q)€IZXIZ*  tq x=p/q
Or on sait que P_q(cos(Pix)=cos(pi*p)=(-1)^p avec P_q le q-ème polynôme de Tchebychev.
On peut alors écrire P_q de la forme 2^(q-1)x^q+Q(x) avec Q un polynôme à coefficients entiers  de degré inférieur ou égal à n-1.
Supposons que cos(pix) est rationnel non nul alors  il existe (a;b)€IZ*XIN* avec pgcd(a;b)=1 tq cos(pix)=a/b
et donc 2^(q-1)a^q+b^qQ(x)=(-1)^p*b^q alors  b/2^(q-1)*a^q  donc b=2b' ce qui donne 2b'/a^q
et par conséquent b'=1  d'ou cos(pix)=a/2  . le a ne peut prendre que -2:-1;1;2 s'ajoute à ceci le cas ou a=0 alors les valeurs possibles de cos(pix) sont {-1;-1/2;0;1/2;1}. La tache donc devient facile pour retrouver les x .

bien joue a vous d'en proposer un autre

Exercice 15:
Montrer que si P est un polynôme de degré n à coefficients dans IR et scindé sur IR alors (n-1)P'²>=nPP"

(pour tout j et i m_j<n_m_i) par reordennement on trouve que c negatif et c ce qu il fallait demontrer) sauf erreur bien sur

expert_run a écrit:

Exercice 15:
Montrer que si P est un polynôme de degré n à coefficients dans IR et scindé sur IR alors (n-1)P'²>=nPP"

L'inégalité à démontrer s'écrit .
En écrivant: avec .
Il vient que: et donc: .
Et encore: .
Il faut donc démontrer que: .
Ce qui est vrai d'après l'inégalité de Caushy-Schwartz, .
CQFD.

.

nmo a écrit:

expert_run a écrit:

Exercice 15:
Montrer que si P est un polynôme de degré n à coefficients dans IR et scindé sur IR alors (n-1)P'²>=nPP"

L'inégalité à démontrer s'écrit .
En écrivant: avec .
Il vient que: et donc: .
Et encore: .
Il faut donc démontrer que: .
On a selon l'inégalité de Caushy-Schwartz, .
Et il est trivial que .
Le résultat découle en sommant ces deux inégalités.
CQFD.

je vois pas pk il y a un a_i^2 quand vous derivez

galillee56 a écrit:

je vois pas pk il y a un a_i^2 quand vous derivez  

Attennds un peu, je vais éditer mon message.
Tu peux proposer un exercice, car tu m'a devancé.

nmo a écrit:

expert_run a écrit:

Exercice 15:
Montrer que si P est un polynôme de degré n à coefficients dans IR et scindé sur IR alors (n-1)P'²>=nPP"

L'inégalité à démontrer s'écrit .
En écrivant: avec .
Il vient que: et donc: .
Et encore: .
Il faut donc démontrer que: .
Ce qui est vrai d'après l'inégalité de Caushy-Schwartz, .
CQFD.

ok ca marche bien joue a vrai dire j'ai pas d'exercice interressant donc vas y

Revenons à l'analyse:
Exercice 16:
Soient continues telles que .
1)On suppose que .
Montrer que toute solution sur de l'équation différentielle admet la limite 0 en .
2)On suppose ici que .
Montrer qu’il existe une solution et une seule sur de l'équation différentielle qui admet la limite 0 en .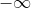
Bonne chance.

1-

meme raisonnement pour la seconde

galillee56 a écrit:

(pour tout j  et i m_j<n_m_i) par reordennement on trouve que c negatif et c ce qu il fallait demontrer) sauf erreur bien sur  

Excuse-moi, mais je n'ai strictement rien compris à votre solution , pourrais-tu clarifier, ou mieux rédiger.

Mehdi.O a écrit:

galillee56 a écrit:

(pour tout j  et i m_j<n_m_i) par reordennement on trouve que c negatif et c ce qu il fallait demontrer) sauf erreur bien sur  

Excuse-moi, mais je n'ai strictement rien compris à votre solution , pourrais-tu clarifier, ou mieux rédiger.

c la meme que celle proposer par nmo le truc est de voir p'/p sauf que a la fin j ai pas utlise cauchy

galillee56 a écrit:

Mehdi.O a écrit:

galillee56 a écrit:

(pour tout j  et i m_j<n_m_i) par reordennement on trouve que c negatif et c ce qu il fallait demontrer) sauf erreur bien sur  

Excuse-moi, mais je n'ai strictement rien compris à votre solution , pourrais-tu clarifier, ou mieux rédiger.

c la meme que celle proposer par nmo le truc est de voir p'/p sauf que a la fin j ai pas utlise cauchy

Bah, je ne vois aucune ressemblance, et puis c'est quoi m à l'avant dernière ligne, et les inégalités que tu as utilisé pour majorer ...
Et pour ta solution à l'exercice d'analyse, on a A(t)-A(x)>=t-x, et non l'inverse

c pas m c'est m indice j et A(t)-A(x)<t-x pour t<x je l ai dit ^^