| | direction mp mp* |  |
|
+11MohE Saiichi aissa expert_run kalm seledeur tahasinbad abdelbaki.attioui Mehdi.O nmo galillee56 15 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 15 Juil 2013, 16:29 Lun 15 Juil 2013, 16:29 | |
| - galillee56 a écrit:
- c pas m c'est m indice j et A(t)-A(x)<t-x pour t<x je l ai dit ^^
Ah d'accord merci, mais tu devrais écrire des phrases dans tes solutions  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 15 Juil 2013, 16:32 Lun 15 Juil 2013, 16:32 | |
| okk  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 15 Juil 2013, 16:39 Lun 15 Juil 2013, 16:39 | |
| Exo 17:nature de la serie de terme general  p_n etant le n-ieme nombre premier | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 15 Juil 2013, 17:23 Lun 15 Juil 2013, 17:23 | |
| - galillee56 a écrit:
- 1-
 Je ne vois pas comment se fait la dernière majoration! - galillee56 a écrit:
- meme raisonnement pour la seconde
Non, ce n'est pas la même chose. On ne travaille pas dans le même domaine, et on cherche à montrer en plus que la solution qui vérifie ces conditions est unique!! | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 15 Juil 2013, 17:43 Lun 15 Juil 2013, 17:43 | |
| - nmo a écrit:
- galillee56 a écrit:
- 1-
 Je ne vois pas comment se fait la dernière majoration!
- galillee56 a écrit:
- meme raisonnement pour la seconde
Non, ce n'est pas la même chose.
On ne travaille pas dans le même domaine, et on cherche à montrer en plus que la solution qui vérifie ces conditions est unique!! vous avez tout a fait raison je suis dsl pour mes erreurs c que je suis un peu fatigue bref  elle existe en - inf vaut 0 vu que e^{-A(x)}=>+ inf alors elle unique | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 00:34 Mar 16 Juil 2013, 00:34 | |
| - galillee56 a écrit:
- Exo 17:
nature de la serie de terme general 
p_n etant le n-ieme nombre premier Soit ^{E(\sqrt{k})}}{P_k}) . Intéressons-nous, pour apporter des simplification dans les sommes, à la suite extraite: ^2})_n) . On a: ^2}=\sum_{k=1}^{(n+1)^2}\frac{(-1)^{E(\sqrt{k})}}{P_k}) . D'où: ^2}=\sum_{i=1}^{n}\sum_{k=i^2}^{(i+1)^2-1}\frac{(-1)^{E(\sqrt{k})}}{P_k}=\sum_{i=1}^{n}\sum_{k=i^2}^{(i+1)^2-1}\frac{(-1)^i}{P_k}) . Et ainsi: ^2}=\sum_{i=1}^{n}(-1)^i\sum_{k=i^2}^{(i+1)^2-1}\frac{1}{P_k}=\sum_{i=1}^{n}(-1)^i.u_i) . Donc ^2}) est une série alternée de la suite ^2-1}\frac{1}{P_k}) . Mais, puisque la suite _i) est positive et croissante, elle ne peut pas avoir la limite 0 quand i tend vers  . Ainsi, selon le théorème des séries alternées, ^2}=\sum_{i=1}^{n}(-1)^i.u_i) diverge. Et par conséquent, _n) diverge. Donc, la série en question diverge. Sauf erreurs.
Dernière édition par nmo le Mar 16 Juil 2013, 09:15, édité 1 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 01:38 Mar 16 Juil 2013, 01:38 | |
| je ne vois pas pourquoi elle est croissante ? | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 12:15 Mar 16 Juil 2013, 12:15 | |
| - galillee56 a écrit:
- Exo 17:
nature de la serie de terme general 
p_n etant le n-ieme nombre premier Indication : il existe a et b >0 tels que : pour tout n>1, a n ln(n) =< p_n =< b n ln(n) | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 12:28 Mar 16 Juil 2013, 12:28 | |
| - abdelbaki.attioui a écrit:
- galillee56 a écrit:
- Exo 17:
nature de la serie de terme general 
p_n etant le n-ieme nombre premier
Indication : il existe a et b >0 tels que :
pour tout n>1, a n ln(n) =< p_n =< b n ln(n) exact plus precisement a=2/5 et b=3 on peut utiliser cette indication sans avoir a la prouver | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 15:28 Mar 16 Juil 2013, 15:28 | |
| Bon je continue le travail commencé par Mr nmo .On montre alors que la série en question est comprise entre deux suites extraites de la forme S_(n+1)^2 qui convergent vers la même limite puisque (u_i) est décroissante et de limite nulle d'après l'indication de Mr abdelbaki.attioui.
Exo 18
a) Soient a et b deux réels avec a différent de 0 et 1. Trouver les f€ C_1(IR;IR) telles que: pour tout x de IR; fof(x)=ax+b.
b)Trouver les f€C_0(IR;IR) telles que: pour tout x de IR fof(x)=e^x. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 17:05 Mar 16 Juil 2013, 17:05 | |
| - expert_run a écrit:
- Bon je continue le travail commencé par Mr nmo .On montre alors que la série en question est comprise entre deux suites extraites de la forme S_(n+1)^2 qui convergent vers la même limite puisque (u_i) est décroissante et de limite nulle d'après l'indication de Mr abdelbaki.attioui.
Exo 18
a) Soient a et b deux réels avec a différent de 0 et 1. Trouver les f€ C_1(IR;IR) telles que: pour tout x de IR; fof(x)=ax+b.
b)Trouver les f€C_0(IR;IR) telles que: pour tout x de IR fof(x)=e^x. a) f(ax+b)=af(x)+b f'(ax+b)=f'(x) f' est constante f(x)=cx+d c^2=a cd+d=b on resout! si ca admet une solution ou pas bien sur
Dernière édition par galillee56 le Mar 16 Juil 2013, 17:56, édité 1 fois | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 17:30 Mar 16 Juil 2013, 17:30 | |
| - galillee56 a écrit:
- expert_run a écrit:
- Bon je continue le travail commencé par Mr nmo .On montre alors que la série en question est comprise entre deux suites extraites de la forme S_(n+1)^2 qui convergent vers la même limite puisque (u_i) est décroissante et de limite nulle d'après l'indication de Mr abdelbaki.attioui.
Exo 18
a) Soient a et b deux réels avec a différent de 0 et 1. Trouver les f€ C_1(IR;IR) telles que: pour tout x de IR; fof(x)=ax+b.
b)Trouver les f€C_0(IR;IR) telles que: pour tout x de IR fof(x)=e^x. a) f(ax+b)=af(x)+b
f'(ax+b)=f'(x)
f' est constante f(x)=cx+d c^2=a cd+d=b on resout! si ca admet une solution ou pas bien sur
b) e^(f(x))=f(x) e^x<x+1 Pourquoi f' est constante. Pour la question b) j'en ai rien compris !! | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 16 Juil 2013, 17:45 Mar 16 Juil 2013, 17:45 | |
| on itere f'(ax+b)=f'(x) donc f'((a^n)x+b(((a^n)-1)/a-1)=f'(x) en fait en suppose que a est dans ]0,1[ n tend vers l inf f' est constante si a est dans ]1, inf[ f'(x)=f'((x-b)/a) f' constante dans tout les cas
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 17 Juil 2013, 18:43 Mer 17 Juil 2013, 18:43 | |
| - expert_run a écrit:
- Exo 18
b)Trouver les f€C_0(IR;IR) telles que: pour tout x de IR fof(x)=e^x. Je pense qu'on ne peut pas déterminer f explicitement! J'ai beau cherché, mais en vain... Je cite ici les propos d'une certaine personne qui propose une réponse en ce sujet:   . Passons à un autre exercice, en attente d'une solution complète pour cette question, de la part de "expert_run", s'il y en a une bien sûr! | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 18 Juil 2013, 00:10 Jeu 18 Juil 2013, 00:10 | |
| Voici la solution que j'ai entre mes mains.   Pour l'instant j'en ai aucun exercice à poster . | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 18 Juil 2013, 00:58 Jeu 18 Juil 2013, 00:58 | |
| Je vous propose celui la.
EXO 19:
Soit (a_k)_k≥0 ∈ IR^IN. On note D_n le déterminant de la matrice (a_|i-j|)1≤i,j≤n. Montrer que D_(n-2)*D_n ≤ [D_(n-1)]^2. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 18 Juil 2013, 16:54 Jeu 18 Juil 2013, 16:54 | |
| en attendant une illumination ou une reponse pour cette exo on continue notre route vers mp mp* je propose celui ci sur les groupes
Exo 20
soit G un groupe de cardinal 2n avec n dans N et H et K deux ss groupe de G tel H inter K ={e} (element neutre) et card(H)=card(K)=n trouver n | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 00:09 Ven 19 Juil 2013, 00:09 | |
| - galillee56 a écrit:
- en attendant une illumination ou une reponse pour cette exo on continue notre route vers mp mp* je propose celui ci sur les groupes
Exo 20
soit G un groupe de cardinal 2n avec n dans N et H et K deux ss groupe de G tel H inter K ={e} (element neutre) et card(H)=card(K)=n trouver n Il est clair que l'intersection de  ,  et  est deux à deux vide. Ces trois ensembles sont des parties de  , tel que la somme de leurs cardinaux est de 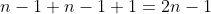 . Ainsi, il existe un autre élément de  , noté  , tel que 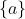 et les trois ensembles ci-dessus forment une partition de  . Puisque  et  un groupe, il faut que  admette un inverse. Cet inverse n'appartiendra plus à  ou à 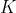 ; car sinon  sera un élément de l'un d'eux; constituant ainsi une contradiction. Il s'ensuit sonc que l'inverse de  est  . On peut donc définir un sous groupe de  formé par les éléments de  et de l'élément  . Il est clair que c'est un sous groupe sans entrer dans les détails... Ce sous groupe est de cardinal 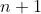 . Le théorème de Legendre affirme que ce cardinal divise celui du groupe  , i.e: 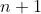 divise 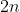 , et cela n'est vérifié que pour 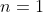 . Sauf erreurs. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 00:40 Ven 19 Juil 2013, 00:40 | |
| Je ne vois pas comment vous creer un tel sous est ce que vous le faite en multipliant les element de H par a mais si vous faite ainsi je vois pas c quoi l inverse de ah par exemple | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 00:49 Ven 19 Juil 2013, 00:49 | |
| - galillee56 a écrit:
- Je ne vois pas comment vous creer un tel sous est ce que vous le faite en multipliant les element de H par a mais si vous faite ainsi je vois pas c quoi l inverse de ah par exemple
Cet ensemble contient les éléments de  et de 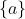 . Appelons . la loi définie dans le groupe  . . est associative dans le nouveau ensemble, noté  . Tout élément de cet ensemble est symétrique (le symétrique de a est lui même, tandis que chaque élément de H a un inverse qui est bien défini vu que H est un sous groupe). | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 01:22 Ven 19 Juil 2013, 01:22 | |
| je suis desole M.nmo je vois vraiment pas pk c un groupe?
recapitulons on rajoute a a H donc si h est dans H ah est dans H_a ah=h_i ou ah=a donc h=e ou a est dans H donc ce n est pas un groupe est de plus l inverse de ah serai h^(-1)a mais on suppose que vous mulplier a droite ou a gauche et n=2 verifie pour cela je prend a dans H tel que a^2=e et b dans K tq b^2=e et donc H={e,a} et K={e,b} on prend tout les element de G verifie a^2=e donc on trouve G est commutatif donc ab=ba G={e,a,b,ab} | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 12:47 Ven 19 Juil 2013, 12:47 | |
| - galillee56 a écrit:
- je suis desole M.nmo je vois vraiment pas pk c un groupe?
recapitulons on rajoute a a H donc si h est dans H ah est dans H_a ah=h_i ou ah=a donc h=e ou a est dans H donc ce n est pas un groupe est de plus l inverse de ah serai h^(-1)a mais on suppose que vous mulplier a droite ou a gauche et n=2 verifie pour cela je prend a dans H tel que a^2=e et b dans K tq b^2=e et donc H={e,a} et K={e,b} on prend tout les element de G verifie a^2=e donc on trouve G est commutatif donc ab=ba G={e,a,b,ab} Je corrige donc: On considère  en tant que sous groupe de  . Il est connu que }=\frac{\text{Card}{H}.\text{Card}{K}}{\text{Card}{(H\cap K)}}=\frac{n.n}{1}=n^2) . Puisque l'ordre du sous groupe divise celui du groupe, on trouve que:  et cela n'est vérifié que losque 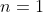 ou 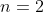 . Dans le premier cas, on prend:  et  tel que l'inverse de a est lui même. Dans le second cas, on prend ce que tu as dit en rouge. J'espère que c'est juste cette fois. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 13:30 Ven 19 Juil 2013, 13:30 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 16:39 Ven 19 Juil 2013, 16:39 | |
| Je propose donc: Exercice 21:Soit  une partie de 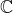 non vide et finie et telle que: : z^2+z+1\in E) et : z^2-z+1\in E) . Determinez E. Bonne chance.P.S: Cet exercice figure dans un devoir surveillé de MPSI Rabat de 2001 (avec des questions préliminaires bien sûr). | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 19 Juil 2013, 17:33 Ven 19 Juil 2013, 17:33 | |
| les orbites de f(z)=z²+z+1 aux points de E sont finis .... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  | |
| |
|
  | |
| | direction mp mp* |  |
|
