direction mp mp*

Exo 55:
Trouver les triplets (m,n,p)€IN^3 tq cos(pi/m)+cos(pi/n)=cos(pi/p)

si m>2 et n>2 bon c pas possible
m=2 n=p
n=2 m=p
m=n=p=2
si m=1 p vaut forcement 1 et n=2

exo 56
soit G un groupe fini et m le plus petit entier tq (x_1,x_2,...x_m) soit generateur de G montrer que card(G)>=2^m

galillee56 a écrit:

si m>2 et n>2 bon c pas possible
m=2 n=p
n=2 m=p
m=n=p=2
si m=1 p vaut forcement 1 et n=2

Comment tu as prouvé que ce n'est pas possible? Il faut détailler.
Pour les autres cas, c'est bon.

si m>2 et n>2 alors m>=3 et n>=3 donc cos(pi/n)+cos(pi/m)>=1 soit cos(pi/p)>=1 impossible

Solution exo 56
Il est évident que card de G est minimal si tout élément de G est d'odre 2( tout élément est l'inverse de lui même) alors dans ce cas cardG=card{prod x_i^(a_i)} avec a_i dans {0,1} alors cardG=sum(k de 0  à m) C( k,m)=2^m donc card(G)》2^m

exo57:
soit k dans N calculer dans Z/pZ som(x^k, x parcourant Z/pZ) p premier

galillee56 a écrit:

exo57:
soit k dans N calculer dans Z/pZ som(x^k, x parcourant Z/pZ) p premier

soit P(X)=X^(p_1)-1 ;  par le petit théorème de fermat P admet 1/;..,(p-1)/  (avec x/la classe d'equivalence de x) .
notons S_k la somme en question, on remarque alors par l utilisation de fermat  que S_k=S_r avec r le reste de la division euclidienne de k par p-1.
par application des sommes de newton on obtient:
S_k=(p-1)/ si k=0 mod(p-1) et 0/ sinon.

expert_run a écrit:

galillee56 a écrit:

exo57:
soit k dans N calculer dans Z/pZ som(x^k, x parcourant Z/pZ) p premier

soit P(X)=X^(p_1)-1 ;  par le petit théorème de fermat P admet 1/;..,(p-1)/  (avec x/la classe d'equivalence de x) .
notons S_k la somme en question, on remarque alors par l utilisation de fermat  que S_k=S_r avec r le reste de la division euclidienne de k par p-1.
par application des sommes de newton on obtient:
S_k=(p-1)/ si k=0 mod(p-1) et 0/ sinon.

bien joue expert-run
voici un exo un peu plus subtil
exo 58:
prouver que toute matrice de trace nul est semblable a une matrice de diagonal nul.

galillee56 a écrit:

voici un exo un peu plus subtil
exo 58:
prouver que toute matrice de trace nul est semblable a une matrice de diagonal nul.

L'exercice est déjà proposé ici dans le forum:
https://mathsmaroc.jeun.fr/t13003-matrice-de-trace-nulle-et-matrice-a-diagonale-nulle.
Que quelqu'un propose un nouvel exercice. Et merci.

oral central (59) : soit,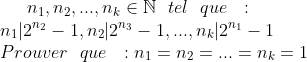

nmo a écrit:

galillee56 a écrit:

voici un exo un peu plus subtil
exo 58:
prouver que toute matrice de trace nul est semblable a une matrice de diagonal nul.

L'exercice est déjà proposé ici dans le forum:
https://mathsmaroc.jeun.fr/t13003-matrice-de-trace-nulle-et-matrice-a-diagonale-nulle.
Que quelqu'un propose un nouvel exercice. Et merci.

desole nmo j'avais pas remarque

Oty a écrit:

oral central (59) : soit,

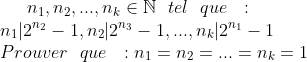
Solution exercice 59:
On suppose que tout les n_i sont différents de 1.
Soient p_i le plus petit premier diviseur de n_i et  a_i le plus petit entier non nul tq 2^(a_i)=1 mod(p_i) ( un tel élément existe puisque par le petit théorème de fermat l'ensemble  {k/2^k=1mod(p_i)} est non vide; il contient p_i-1}
et puisque  2^(n_(i+1))=1[p_i] alors  a_i divise n_(i+1) et p_i -1
donc p_(i+1)<=a_i<p_i ce qui confirme que la suite des p_i est strictement décroissante et par suite p_1<p_1****absurde*****
Alors il existe au moins un n_i égal à 1. (Et par une récurrence nous obtenons que n_i=1 pour tout i entre 1 et k)

Exercice 60:
On rappelle que si G est un groupe fini et H un sous groupe de G; l'indice de H dans G est l'entier [G:H]=card(G)/card(H)
Soit p>=5 un nombre premier. Si H est un sous groupe du groupe symétrique S_p tel que [S_p:H]<=p-1, montrer que [S_p:H]€{1;2}.

expert_run a écrit:

donc p_(i+1)<=n_(i+1)<p_i

tu pourrais expliqué cette inégalité , pk n_(i+1) < p_{i} ?

Oty a écrit:

expert_run a écrit:

donc p_(i+1)<=n_(i+1)<p_i

 
tu pourrais expliqué cette inégalité , pk  n_(i+1) < p_{i} ?

je veux dire p_(i+1)<=a_i<p_i

exo61
soit K un corps fini de cardinal q trouver le card(Gln(K)) et card(Sln(K))
Sln(K): ensemble de matrice de determinant 1 et a coeff dans K

expert_run a écrit:

Exercice 60:
On rappelle que si G est un groupe fini et H un sous groupe de G; l'indice de H dans G est l'entier [G:H]=card(G)/card(H)
Soit p>=5 un nombre premier. Si H est un sous groupe du groupe symétrique S_p tel que [S_p:H]<=p-1, montrer que [S_p:H]€{1;2}.

On a d'emblée: , donc .
On considère un cycle 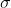d'ordre , et on considère les sous groupes: , 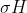, ... et .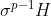
Il est très bien connu que tous ces sous groupes ont le même cardinal.
Si ces groupes étaient deux à deux disjoints, on aurait: .
Cela étant absurde. On déduit donc que ces sous groupes ne sont pas deux à deux disjoints.
En choisissant, un élément commun à et à 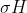, on déduit que .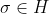
Ainsi, on a prouvé que contient tous les cycles d'ordre .
On sait aussi que de n'importe quel produit de cycles d'ordre , peut se mettre sous la forme d'un produit de transpositions.
Et que le produit de deux transpositions est soit un cycle d'ordre 3 ou un produit de cycles d'ordre 3.
Donc, tous les éléments du sous groupe sont des produits de cycles d'ordre 3.
Autrement dit, les cycles d'ordre 3 sont une partie génératrice de .
Deux cas se présentent:
--- Soit tous les éléments de sont des produits pairs de cycles d'ordre 3.
Cela veut dire que chaque élément de est de signature 1.
Donc 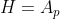, où 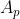est le sous groupe alternée.
On sait que , et dans ce cas, l'indice de est 2.
--- Sinon, 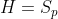, et dans ce cas l'indice de est 1.
CQFD.
Sauf erreurs.

galillee56 a écrit:

exo61
soit K un corps fini de cardinal q trouver le card(Gln(K)) et card(Sln(K))
Sln(K): ensemble de matrice de determinant 1 et a coeff dans K

--- Commençons par le groupe: .
Il est clair qu'il y a 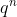vecteurs différents de longueur construits à partir des éléments de .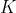
Travaillons sur les lignes d'une matrice d'ordre :
Il faut choisir les ses vecteurs lignes parmi les vecteurs possibles de telle sorte qu'ils soient libres dans leurs ensemble.
La seule contrainte imposée sur le premier vecteur (celui de la première ligne), est de ne pas être nul.
On peut donc le choisir de 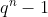manières.
Pour le deuxième colonne, on doit tout simplement choisir un vecteur qui n'appartient pas au sous espace vectoriel engendré par le vecteur de la premiere ligne.
Et puisque le sous espace vectoriel engendré par le vecteur de la première ligne est de cardinal , on peut faire ce choix avec 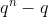manièrères.
Et on continue ainsi...,
La réponse est alors: .
--- Maintenant, le groupe :
Puisqu'un déterminant est une forme multilinéaire sur l'ensemble des éléments de , il peut prendre les valeurs possibles.
Mais, on s'intéressa ici à ce que le déterminant soit égale à 1.
Il est clair aussi que si le determinant n'est pas nul, il peut prendre 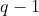valeurs, et cela d'une manière uniforme.
C'est à dire le nombre de matrice à déterminant égale à 1, est égale au nombre de matrice dont le determinant est égale à n'importe quel élément non nul de .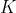
Dans la première question, on a calculé le nombre de matrice dont le determinant est non nul.
Donc, le nombre de matrices dont le déterminant est 1 est égale à: .
Sauf erreurs.

bien joue nmo c'est les bonnes solutions pour les 2 exo

M nmo vous postez un exo ou bien je m'en occupe ?

galillee56 a écrit:

M nmo vous postez un exo ou bien je m'en occupe ?

Bon, je n'ai pas d'exercices intéressants pour le moment. Tu peux t'en occuper, et merci.

Exo 62: soit A dans Mn(R) montrer qu'il existe U et V dans On(R) et D diagonale tq A=UDV

Vz a écrit:

 Autre solution (52)

L'inégalité étant équivalente à  avec  on peut alors sans perte de généralité supposer que , il suffit donc de démontrer avec cette hypothèse que . Posons , remarquons que  donc une simple intégration par partie donne , le résultat est donc immédiat dès que l'on montre que  puisque  par hypothèse. Or cela découle de la convexité de  puisque  car en effet   solution (62): Si la matrice  est inversible alors la matrice  est symétrique définie positive, on peut donc trouver une matrice orthogonale  est une matrice diagonale  telles que , il suffit donc de poser  et de remarquer que cette matrice est orthogonale, si maintenant  n'est pas inversible on peut alors introduire une suite  de matrices inversibles tendant vers  et introduire également la suite  telle que  on peut facilement montrer que cette suite est bornée donc on peut en extraire une suite convergente, comme  et l'espace des matrices diagonaux sont fermés on peut on en déduire directement le résultat

bien joue Vz
exo63
soit A et B dans Mn(Z) tel que pour tout k dans {0,1,...,2n} A+kB soit dans Gln(Z) calculer det(A) et det(B).