direction mp mp*

galillee56 a écrit:

exo63
soit A et B dans Mn(Z) tel que pour tout k dans {0,1,...,2n} A+kB soit dans Gln(Z) calculer det(A) et det(B).

Le problème est classique, et en voici une solution:
Il est facile de remarquer que si est une matrice de , alors son determinant est ou bien 1, ou bien -1.
En effet, on aura: 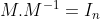, donc .
Il s'ensuit que est un entier divisant 1, donc ou .
Pour le problème proposé, il suffit de considérer le polynôme de degré 2n, défini par: .
Ce polynôme admet 2n+1 racines selon l'hypothèse et le lemme démontré, il est donc nul.
Et on déduit donc que: .
Et, donc .
---Pour 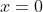, il s'ensuit immédiatement que: , soit ou .
---On a aussi: , donc .
Et lorsqu'on fait tendre x vers , il vient que: , soit .
Sauf erreurs.

Vz a écrit:

Je poste cet exercice à fin de respecter le marathon (64): Soient  et  dans. On suppose que . Montrer :

H est de rend 1 donc soit C une colonne tq H=(a_1C|a_2C|...a_nC)
donc det(A+H)=det(C_1+a_1C|C_2+a_2C|..|C_n+a_nC)=det(A)+som(det(C_1|C_2..|C_{i-1}|a_iC|C_{i+1}..|C_n), i=1..n) cette somme on l appelle S donc det(A+H)=det(A)+S et det(A-H)=det(A)-S donc det(A+H)det(A-H)=det(A)^2-S^2<det(A)^2

Oui bien joué galillee56, tu peux poster un nouveau exercice, j'espère qu'il sera intéressant

exo65
soit f C1 de [1,+inf[->R tel que f'/f tend vers -inf en +inf montrer que que la serie de terme general f(n) et trouver un equivalent de la somme(f(k),k=n...inf)

exo66
Soit p un nombre premier tel que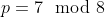
Montrer que :

Tel que 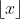la partie entière de x.

Solution 65 :
Lorsque tu écris  je suppose que l'énoncé sous entend que  ne s'annule pas sur un voisinage en , étant continue elle garde un signe constant sur un intervalle de la forme  , quitte à changer  en  on peut également supposer que  est positive sur , avec ces hypothèses la fonction  est bien définie sur  et est de classe , et on a donc pour tout ,        qui tend vers , il existe donc  tel que pour tout  ainsi pour tout x>B 
 
donc  si bien que  donc la série de terme générale  converge, et le reste partiel
  
existe, pour chercher un équivalent de ce reste on va introduire à nouveau la fonction  définie sur  par , pour tout  on peut dire que  pour un certain , la suite  tend évidemment vers l'infini, par conséquent  tend vers  donc on peut affirmer que , comme la série de terme général   positif à partir d'un certain rang converge, alors
  
cela prouve que  donc 

je souhaite une agréable rentrée a tout ceux qui sont en prepa bref il y en aurai peut etre plus assez de temps pour ce forum bref voici un exo X assez sympas
soit k dans {1,...n} et n_k le reste de la division de n par k et p_n la probabilité que n_k>=k/2. calculer p_n et trouver la limite de p_n quand n tend vers l infini bonne chance

salut qui veut terminer ce marathon ?

Saiichi a écrit:

salut qui veut terminer ce marathon ?

Il y a deux exercices sans solutions dans cette page même (L'exercice 66 et celui de galillee qui doit porter le numéro 67). Je propose un autre exercice, afin de revivre le topic:
Exercice 68:
Soit un polynôme de degré  .
1- Montrez que si est scindé sur , alors 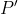l'est aussi.
2- Montrez que si est scindé sur , alors .
3- Montrez que si est scindé sur , alors .
Bonne chance.
P.S: La question 2 est déjà proposée dans ce marathon.

ca fais plaisir de reprendre ce topic
donc en reponse a l'exo 68

Spoiler: