| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: monde des inégalités Sujet: monde des inégalités  Dim 29 Déc 2013, 19:59 Dim 29 Déc 2013, 19:59 | |
| lançant un sujet consacré aux olympiades. Comme d’habitude numéroter les exercices. EX1: 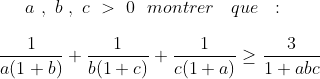 c'est facile mais c'est pour commencer
Dernière édition par L-W-P le Dim 29 Déc 2013, 20:18, édité 2 fois | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 29 Déc 2013, 20:26 Dim 29 Déc 2013, 20:26 | |
| EX2:
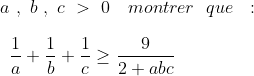 autre exo habitué | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 13:06 Lun 30 Déc 2013, 13:06 | |
| Pour le 2!!!
-Démontrer que le polynôme x^3 -3x + 2 est toujours positif dans R+ (la racine évidente est 1).
-En déduire que pour tout a, b et c dans R+, 3racinecubVabc <= abc + 2
-En conclure que la moyenne géométrique de a, b et c est inférieure ou égale à (abc+2)/3, et donc la moyenne harmonique est également inférieure à (abc+2)/3
-Inverser les deux côtés, puis multiplier par 3, pour trouver l'inégalité voulue...
Je poste?
| |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 13:25 Lun 30 Déc 2013, 13:25 | |
| Solution EX2: Par I.A.G:  il suffit de démontrer que  Par I.A.G:   d'où le résultat. | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 13:26 Lun 30 Déc 2013, 13:26 | |
| à vous de poster maintenant .
B.N: numéroter et utiliser latex | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 14:16 Lun 30 Déc 2013, 14:16 | |
| Ah non, je passe!!
J'veux de quoi m'entraîner pendant ces vacances^^!!
A'vous l'honneur!!
(Un indice pour le 1?)
| |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 14:37 Lun 30 Déc 2013, 14:37 | |
| Puisque personne n'a proposé d'exercice, et pour faire un peu vite je propose cette equation fonctionelle (un peu facile pour commencer).
EXO 3:
Determinez toutes les applications de R vers R verifiant:
f(x²+y)=f(x)+f(y²) pour tout (x,y) de R² | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 | |
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 15:39 Lun 30 Déc 2013, 15:39 | |
| Réponse de l'EXO 3:
en substituant y = 0, on trouve f(x) = f(x²) = f(x^4) = .... = f(x^2n) pour tout n dans N
en substituant x² = -y on trouve -f(x) = f(x^4)
D'où f(x) = -f(x) pour tout x dans R.
la solution est la fonction nulle.
Pareil, je ne poste pas d'exo. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 16:03 Lun 30 Déc 2013, 16:03 | |
| C'est juste. A toi de Poster cette fois ^^ | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 30 Déc 2013, 17:02 Lun 30 Déc 2013, 17:02 | |
| | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 31 Déc 2013, 14:50 Mar 31 Déc 2013, 14:50 | |
| C'est bizarre, je ne l'ai toujours pas...Soit je me suis égaré, soit c'est plus difficile que prévu (z'eu vote pour la première option  ) Bon, en attendant la solution pour le 1er, voilà une bonne inégalité, de quoi nous entraîner pour les factorisations. a, b et c sont les côtés d'un triangle, prouver que: ^2&space;\geqslant&space;2(a^4+b^4+c^4)) | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 10:07 Mer 01 Jan 2014, 10:07 | |
| j' ai déjà prévenu de numéroter les exercices EXO 4
a,b,c sont des longueurs d'un triangle, prouver que  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 12:16 Mer 01 Jan 2014, 12:16 | |
| My ugly method for the forth Exercice: j'ai besoin de confirmation pour poster un exercice   Sauf Erreur  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 14:20 Mer 01 Jan 2014, 14:20 | |
| Bon En attendant votre confirmation je Poste: EXO 5: soit a,b et c des réels positifs tel que a+b+c+d=1, Montrer que: 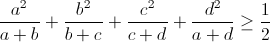 | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 16:51 Mer 01 Jan 2014, 16:51 | |
| WLOG : ordonner les variables, tchebychev, utiliser 4(a²+b²+c²+d²) ≥(a+b+c+d)² et 2(a+b+c+d)(∑(1/a+b))≥ 16 . A vous de proposer un exo | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 16:57 Mer 01 Jan 2014, 16:57 | |
| A toi de proposer, c'est bien toi qui a trouvé la réponse ^^ | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 17:13 Mer 01 Jan 2014, 17:13 | |
| #Legend-Cruch: Ta méthode paraît correcte, je ne suis pas au courant des nouvelles propriétés de la trigo de cette année...En attendant qu'un autre puisse corriger, voici ma proposition, et j'espère qu'elle vous sera utile à tous!!
Nouvelle factorisation, aussi (enfin, presque) importante que les identités remarquables:
(a²+b²+c²)² - (a^4 + b^4 + c^4) = (a+b+c)(a+b-c)(a-b+c)(-a+b+c)
on a a, b, et c les longueurs d'un triangle, donc les 4 termes du produits sont positifs, d'où l'inégalité!!
P.S: On attend l'EXO 6^^ | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 17:16 Mer 01 Jan 2014, 17:16 | |
| Ta méthode est très bonne et courte. Mais elle n'est pas évidente à trouver ^^ | |
|
  | |
Sketshup
Maître

 Nombre de messages : 85 Nombre de messages : 85
Age : 26
Date d'inscription : 03/11/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 17:17 Mer 01 Jan 2014, 17:17 | |
| Merci!!
Mais maintenant, on peut la trouver facilement!! | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 17:19 Mer 01 Jan 2014, 17:19 | |
| Seledeur, tu veux bien proposer une inégalité? Sinon qui peut en mettre une ? | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 17:20 Mer 01 Jan 2014, 17:20 | |
| D'accord : x,y,z > -1 prouvez que  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 | |
  | |
Zouhair-Evariste
Féru

 Nombre de messages : 40 Nombre de messages : 40
Age : 27
Date d'inscription : 31/08/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 01 Jan 2014, 23:31 Mer 01 Jan 2014, 23:31 | |
| - seledeur a écrit:
- D'accord : x,y,z > -1
prouvez que
 remarquez bien que 1+x²/1+y+z²>= 1+x²/(1+((y²+1)/2)+z²) et puis on substitue par a=x²+1 ... et on obtiendra une inégalité plus facile | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 02 Jan 2014, 02:36 Jeu 02 Jan 2014, 02:36 | |
| Oui, Bravo, Proposes une autre . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
