| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 07 Mar 2014, 14:58 Ven 07 Mar 2014, 14:58 | |
| - DAMP a écrit:
- Vu que Mlle.Elmrini s'est absenté du forum, je vais me pérmettre de poster une inégalité en espérant réanimer le sujet : a,b,c>0
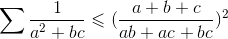 non cette inégalité reste fausse | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 07 Mar 2014, 14:59 Ven 07 Mar 2014, 14:59 | |
| | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 07 Mar 2014, 15:02 Ven 07 Mar 2014, 15:02 | |
| - DAMP a écrit:
- Pour le lemme : Il y a une démonstration classique mais je me suis dis pourquoi ne pas utiliser réordonement puisqu'elle est rarement utilisé donc quand on a l'occasion..
 : :
Par l'inégalité du réordonement : (En considérant un ordre bien sure) 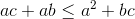
donc
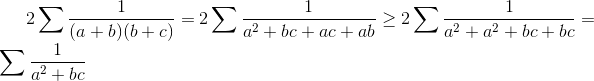
A toi de poster Mlle Elmrini ! je n'ai pas compris bien votre méthode : si a >b >c alors : a²+bc >ab+ac et c²+ab >ac+bc mais pour b on trouve : b^2+ac <ab+bc | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 07 Mar 2014, 15:22 Ven 07 Mar 2014, 15:22 | |
| bon voici la démonstration du lemme 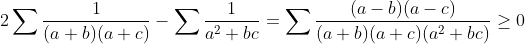 x,y,z>0 tel que x+y+z=1 Montrer que : 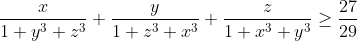 | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 10 Mar 2014, 21:50 Lun 10 Mar 2014, 21:50 | |
| - elmrini a écrit:
- x,y,z>0 tel que x+y+z=1
Montrer que : 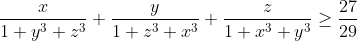 solution : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=52&t=574993&p=3387279#p3387279 EXPLICATION : 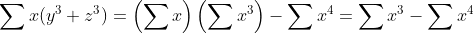 | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 10 Avr 2014, 18:32 Jeu 10 Avr 2014, 18:32 | |
| Pour la survie de ce sujet je propose cette inégalité :
a,b et c appartenant a R tels que a²+b²+c²=2
Montrez que a+b+c =< abc+2
BONNE CHANCE . | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 14 Avr 2014, 15:31 Lun 14 Avr 2014, 15:31 | |
| | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 19 Avr 2014, 12:46 Sam 19 Avr 2014, 12:46 | |
| - bianco verde a écrit:
- Pour la survie de ce sujet je propose cette inégalité :
a,b et c appartenant a R tels que a²+b²+c²=2
Montrez que a+b+c =< abc+2
BONNE CHANCE . voir ici | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 21 Avr 2014, 19:02 Lun 21 Avr 2014, 19:02 | |
| OUI ! a vous de poster une inegalité MR.younesmath2012 ! | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 22 Avr 2014, 12:51 Mar 22 Avr 2014, 12:51 | |
| l'exercice suivant: http://latex.codecogs.com/gif.download?a%7E%2C%7Eb%7E%2C%7Ec%7E%5Cin%7E%5Cmathbb%7BR%7D%7Etq%7E%3A%7Ea%5E2+b%5E2+c%5E2%3D2%7Emontrer%7Eque%7E%3A%5C%5C%5C%5C%5Cbullet%7E%7E%5Cfbox1%7E%7E%20a+b+c%5Cleq%20abc+%5Csqrt%7B4-%5Cfrac%7B5a%5E2b%5E2c%5E2%7D%7B4%7D%7D%7E%7E%7E%28plus%7Eforte%7Eque%7Ea+b+c%5Cleq%20abc+2%7E%29%5C%5C%5C%5C%5Cbullet%7E%7E%5Cfbox2%7E%7E1+abc%28a+b+c%29%3E%200 | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 26 Avr 2014, 15:00 Sam 26 Avr 2014, 15:00 | |
| - younesmath2012 a écrit:
- l'exercice suivant:
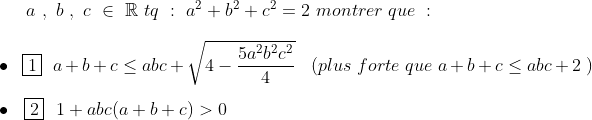 (1) ^2\leq 4-\frac{5a^2b^2c^2}{4}) 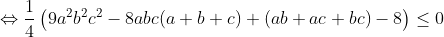 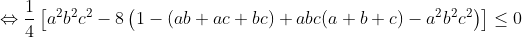 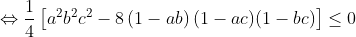 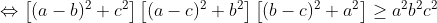 qui est vrai. (2)on a 2 cas 1er cas : 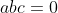 donc : =1>0) 2eme cas :  alors : >1+(a+b+c)(a+b+c-2)=(a+b+c-1)^2) car 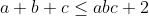 avec l'egalité si et seulement si l'un des trois est nul et les deux autres sont egaux. | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 27 Avr 2014, 12:38 Dim 27 Avr 2014, 12:38 | |
| votre derniere ligne n'est pas juste car a+b+c peut etre negative donc on ne peut pas assurer que abc(a+b+c)>(a+b+c)(a+b+c-2)  merci | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 27 Avr 2014, 16:47 Dim 27 Avr 2014, 16:47 | |
| - younesmath2012 a écrit:
- votre derniere ligne n'est pas juste car a+b+c peut etre negative donc on ne peut pas assurer que abc(a+b+c)>(a+b+c)(a+b+c-2)

merci mmm vous avez raison donc il reste de démontrer l'inégalité dans le cas : a+b+c <0 si abc <0 alors 1+abc(a+b+c) >1>0 si abc >0 on a : a+b+c <0 alors il existe x,y et z positifs tel que : abc=xyz,a+b+c=x-y-z et x²+y²+z²=2 l'inégalité équivalente a : 1+xyz(x-y-z)>0 ou 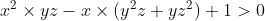 On a : 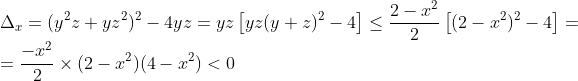 et puisque x,y,z>0 alors 1+xyz(x-y-z)>0. je pense que la solution est complete maintenant. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
