| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 27 Fév 2014, 21:37 Jeu 27 Fév 2014, 21:37 | |
| a,b,c>0 Prouver que : a²+b²+c²+2abc+1>2(ab+ac+bc) | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 | |
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 27 Fév 2014, 22:27 Jeu 27 Fév 2014, 22:27 | |
|  il suffit alors de montrer que  on a  il suffit alors de montrer que  ce qui est vrai http://www.wolframalpha.com/input/?i=3%28x%29%5E%282%2F3%29+-+2x+-1+ | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 27 Fév 2014, 22:52 Jeu 27 Fév 2014, 22:52 | |
| BRAVO M.seledeur
P.S : la dernier inégalité est vrai par am gm x^3+x^3+1>3x² avec x^3=abc
a toi de poster une autre ineq. | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 27 Fév 2014, 23:03 Jeu 27 Fév 2014, 23:03 | |
| a,b,c> 0 tq ab+ac+bc=1 , MQ  | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 27 Fév 2014, 23:52 Jeu 27 Fév 2014, 23:52 | |
| M. Seledeur a écrit: a,b,c> 0 tq ab+ac+bc=1 , MQ 
Avant d'aller m'endormir, je propose une solution que j'ai trouvée dans un livre:  Bonne nuit. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 28 Fév 2014, 09:29 Ven 28 Fév 2014, 09:29 | |
| Cette méthode est vraiment épatante   Je me permet, pour faire vite, de poster un petit exo proposé dans l'entrainement de l'année dernière  Soient a,b,c trois réels strictement positifs tels que  , Montrer Que:  | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 28 Fév 2014, 12:47 Ven 28 Fév 2014, 12:47 | |
| WLOG :  par Chyebechev :  il suffit alors de montrer que  ce qui est vrai . | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 28 Fév 2014, 15:24 Ven 28 Fév 2014, 15:24 | |
| Bravo M. Seledeur et un grand Merci à M. Legend_Crush qui a proposé cet exercice. J'ai une toute petite remarque à propos de l'ordre des variables: on a appris que les inégalités cycliques permettent seulement de définir un plus petit élément ou un plus grand élément.  | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 28 Fév 2014, 16:24 Ven 28 Fév 2014, 16:24 | |
| a,b,c strictement positifs : MQ  | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 28 Fév 2014, 18:30 Ven 28 Fév 2014, 18:30 | |
| | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 28 Fév 2014, 19:03 Ven 28 Fév 2014, 19:03 | |
| a,b,c>0 avec a+b+c=1/a+1/b+1/c Montrer que : ab+bc+ac+abc≥4 | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 13:45 Dim 02 Mar 2014, 13:45 | |
| Posons p = a+b+c et q = abc , alors en utilisant la condition on a pq=ab+bc+ac , il est clair que p≥3, et l'inégalité a montrer est equivalente a q(p+1) ≥ 4 , on a  et en utilisant la condition : a²+b²+c² = p²-2pq, donc schur est equivalente a p³ + 9q ≥ 4qp² donc q(p+1)≥p³(p+1)/(4p²-9) , il suffit alors de montrer que p³(p+1)/(4p²-9) ≥ 4 pour p ≥3 ce qui est vrai http://www.wolframalpha.com/input/?i=%28p%5E3%28p%2B1%29%29%2F%284p%5E2-9%29+from+3+to+4 | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 13:47 Dim 02 Mar 2014, 13:47 | |
| pour  , voir http://www.artofproblemsolving.com/Forum/viewtopic.php?p=2796376&sid=9a77b65305d642c0f3fb32f5e200a7b0#p2796376 | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 14:18 Dim 02 Mar 2014, 14:18 | |
| a,b,c strictement positifs tq a+b+c =1 , MQ  | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 18:25 Dim 02 Mar 2014, 18:25 | |
| | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 18:41 Dim 02 Mar 2014, 18:41 | |
| On a par C-S :  donc il suffit de montrer que 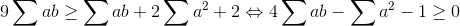 (1) et on a par la condition 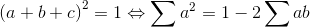 donc (1) <=> 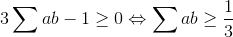 d’où le résultat . | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 19:10 Dim 02 Mar 2014, 19:10 | |
| | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 19:16 Dim 02 Mar 2014, 19:16 | |
|
Dernière édition par DAMP le Dim 02 Mar 2014, 20:04, édité 1 fois | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 19:52 Dim 02 Mar 2014, 19:52 | |
| a,b,c>0 tel que a+b+c=3, montrez que 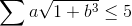 | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 19:55 Dim 02 Mar 2014, 19:55 | |
| pour utiliser chebyshev les 2 sequences doit etre ordonnees de la meme facon ou de facon inverse. on supposant
a>=b>=c on ne pourra pas utiliser chebyshev avec (a;b;c) et (b;c;a) sauf erreur | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 20:05 Dim 02 Mar 2014, 20:05 | |
| Oui tu as raison faute d'innatention  | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 20:31 Dim 02 Mar 2014, 20:31 | |
| | |
|
  | |
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 20:44 Dim 02 Mar 2014, 20:44 | |
| a,b,c,x strictement positifs , MQ  | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Mar 2014, 22:30 Dim 02 Mar 2014, 22:30 | |
| On montre d'abord que 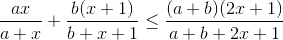 Après avoir developer, l'inégalité est equivalente à:  En utilisant la propriété précédente on trouve : 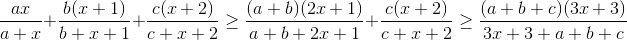 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
