monde des inégalités

Ahmed Taha,


C'est plus facile avec AM-GM

Humber a écrit:

Ahmed Taha,


C'est plus facile avec AM-GM

hhhhh oui bien sur....merci

Prouver que:



ou ... démontrer que :

L'inégalité est fausse ! Prendre a→ oo et b=c<1

Humber a écrit:

L'inégalité est fausse ! Prendre a→ oo et b=c<1

oui vous avez raison   

Ahh donc c'est pour ca hhh ,
Apres développement on arrive a a²b² +b²c² + a²c² +ab+ac+bc ≥ a²bc+b²ac+c²ab+a²+b²+c²  ou encore  (b-c)²(a²-1) + (a-b)²(c²-1)  + (a-c)²(b²-1)  ≥ 0 ce qui est vrai .

L'inégalité avec la valeur absolue est elle aussi fausse...

seledeur a écrit:

Ahh donc c'est pour ca hhh ,
Apres développement on arrive a a²b² +b²c² + a²c² +ab+ac+bc ≥ a²bc+b²ac+c²ab+a²+b²+c²  ou encore  (b-c)²(a²-1) + (a-b)²(c²-1)  + (a-c)²(b²-1)  ≥ 0 ce qui est vrai .

BRAVO voici une autre méthode
on a  (ab-1)²≥(a²-1)(b²-1) car a²+b²≥2ab
et de mm manière pour les autres...
alors je pense que les deux inégalités sont vraies  

Prendre a→ oo et b=c<1 pour la deuxième aussi .

joli la tienne est bien meilleure !
x,y,z ≤1 tq x+y+z=1 , montrez que :

Humber a écrit:

Prendre a→ oo et b=c<1 pour la deuxième aussi .

hhh autre fois vous avez raison  

x y z ne sont pas nécessairement positifs.

legend-crush a écrit:

Elle n'est pas concave sur [0,1] en plus.

oui je viens de le remarquer, elle n'est pas concave sur [0;1] en entier  :/
http://www.wolframalpha.com/input/?i=%281%2F%281%2Bx^2%29%29%27%27&lk=4&num=1&lk=4&num=1

seledeur a écrit:

joli la tienne est bien meilleure !
x,y,z ≤1   tq x+y+z=1 , montrez que :

Je propose une solution usant de la méthode de la tangente:
On démontre que .
En effet, cela équivaut à .
En écrivant cette inégalité pour x, y et z de l'énoncé; puis en sommant et en utilisant la condition imposée, on trouve que .
Le cas d'égalité est lorsque .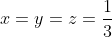
CQFD.
Sauf erreurs.
Que chacun se sente libre de proposer un nouvel exercice.

ce qui est vrai .

Donc

EDIT : Je viens de voir la réponse de nmo, désolé. J'ai utilisé la méthode.

oui bravo !

a,b et c des réels strictement positifs, M.Q :

Bravo Mr Ayman, mais il y a moyen de raccourcir la solution :
Dès la deuxième ligne :


Parce que a²b²+b²c²+c²a² >= abc(a+b+c)

aymas a écrit:

solution:

Humber a écrit:

Bravo Mr Ayman, mais il y a moyen de raccourcir la solution :
Dès la deuxième ligne :


Parce que a²b²+b²c²+c²a² >= abc(a+b+c)

bien joué les amis   
si vous avez un prob pour continuer   

Salut, c'est ce que j'ai trouvé pour le moment :
Prouver que :