| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
seledeur
Féru
 Nombre de messages : 43 Nombre de messages : 43
Age : 28
Date d'inscription : 22/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 05 Jan 2014, 11:10 Dim 05 Jan 2014, 11:10 | |
| a,b,c ∊ (1,2) MQ  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 05 Jan 2014, 13:24 Dim 05 Jan 2014, 13:24 | |
|  1<a,b,c<2 ==> 4b≥4 et sqrt(ac)≤ 4 ==> sqrt(ac)≤4b ==> ac≤ 4b*sqrt(ac). Donc les dénominateurs du LHS sont tous positifs . Ainsi il est possible d'appliquer Cauchy-Shwartz :  Cas d'égalité : a=b=c . | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 05 Jan 2014, 20:20 Dim 05 Jan 2014, 20:20 | |
| | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 | |
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 05 Jan 2014, 21:08 Dim 05 Jan 2014, 21:08 | |
| soient a,b,c>0 tels que abc=1 Montrer que : 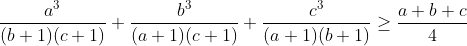 | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 06 Jan 2014, 20:39 Lun 06 Jan 2014, 20:39 | |
|  Parce qu'avec p=a+b+c, p²>=2p+3 <==> (p-3)(p+1)>=0 ce qui est vrai puisque a+b+c>= 3(abc)^(1/3) | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 06 Jan 2014, 21:10 Lun 06 Jan 2014, 21:10 | |
| - Humber a écrit:

Parce qu'avec p=a+b+c, p²>=2p+3 <==> (p-3)(p+1)>=0 ce qui est vrai puisque a+b+c>= 3(abc)^(1/3) Bon méthode voici une autre : 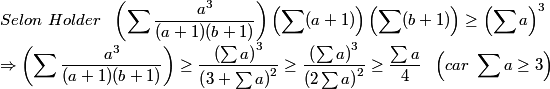 | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 | |
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 07 Jan 2014, 13:32 Mar 07 Jan 2014, 13:32 | |
| Prouver que :  a,b,c étant des longueurs d'un triangle | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 08 Jan 2014, 18:54 Mer 08 Jan 2014, 18:54 | |
| Quelqu'un pourrai éclaircir le passage par C-S dans la démonstration de Humber Svp ? | |
|
  | |
L-W-P
Maître

 Nombre de messages : 238 Nombre de messages : 238
Age : 27
Date d'inscription : 23/09/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 08 Jan 2014, 19:23 Mer 08 Jan 2014, 19:23 | |
| C-S c’est l'inégalité célèbre de Cauchy Schwartz | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 08 Jan 2014, 19:37 Mer 08 Jan 2014, 19:37 | |
| Oui oui je sais bien, mais comment il l'a utilisé pour faire ce passage, je ne vois comment il l'a utilisé | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 | |
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 08 Jan 2014, 20:17 Mer 08 Jan 2014, 20:17 | |
| - DAMP a écrit:
- Quelqu'un pourrai éclaircir le passage par C-S dans la démonstration de Humber Svp ?
It's popularly known as Cauchy-Shwartz inequality in Engel Form. | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 08 Jan 2014, 20:27 Mer 08 Jan 2014, 20:27 | |
| - Ahmed Taha a écrit:
- DAMP a écrit:
- Oui oui je sais bien, mais comment il l'a utilisé pour faire ce passage, je ne vois comment il l'a utilisé
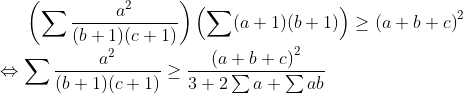 Ah oui c'est plus claire, merci bcp Ahmed Taha ! | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 09 Jan 2014, 16:43 Jeu 09 Jan 2014, 16:43 | |
| | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 09 Jan 2014, 17:01 Jeu 09 Jan 2014, 17:01 | |
| Montrer que : 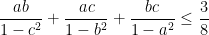 avec a,b,c>0 et a+b+c=1 | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 16:00 Mar 14 Jan 2014, 16:00 | |
|  Mais, avec a=x² ... :  Donc :  Et puisque la fonction x-> x/(x+1) est concave sur IR+ nous avons par Jensen :  . QED . J'aimerais bien, si possible voir ta solution Ahmed Taha. Pour voir seulement s'il y a une solution plus élégante. Merci | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 17:05 Mar 14 Jan 2014, 17:05 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 17:08 Mar 14 Jan 2014, 17:08 | |
| Merci pour le livre, intéressant. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 17:27 Mar 14 Jan 2014, 17:27 | |
| - Humber a écrit:
- Merci pour le livre, intéressant.
c rien  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 16 Jan 2014, 18:16 Jeu 16 Jan 2014, 18:16 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 18 Jan 2014, 23:28 Sam 18 Jan 2014, 23:28 | |
| L'inégalité est équivalente à prouver que : ab+bc+ac+abc≥4 ou encore (a-1)(b-1)(1-c)+a+b+c+2abc≥5 Observons que a,b,c ne peuvent être tous supérieurs ou inférieurs à 1. Supposons donc SPDG que (a,b)≥1 et que 1≥c. Nous avons donc (a-1)(b-1)≥0 et donc (a-1)(b-1)(1-c)+a+b+c+2abc≥a+b+c+2abc Il suffit ainsi de prouver que a+b+c+2abc≥5Si abc≥1 l'inégalité est claire parce que a+b+c≥3 . Si 1≥abc : <==>  Prenons la fonction f: x->p/x+2x avec p²=(ab+bc+ac)²≥3abc(a+b+c)=3(ab+bc+ac) ==> p≥3 et x=abc 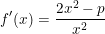 1≥x ==>2x²-p <0 donc f est décroissante sur ]0,1], ainsi f(x)≤f(1) <==> f(x)≥p+2≥5 Donc p/x+2x=(ab+bc+ac)/abc+2abc≥5 ==>a+b+c+2abc≥5. CQFD Finalement je pense que le cas 1≥abc est inutile vu que lorsque(a,b)≥1 et c en est inférieure, abc est systématiquement supérieur ou égal à 1 . Reste à le démontrer. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 19 Jan 2014, 03:21 Dim 19 Jan 2014, 03:21 | |
| n≥2 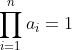 Prouver que : | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 25 Jan 2014, 19:42 Sam 25 Jan 2014, 19:42 | |
| Pour le problème de M. Ahmed TAHA du 9 Janvier 2014, j'ai trouvé une solution dans laquelle on n'utilise que les IAG. Soient a,b et c des réels positifs tel que a+b+c=1. Montrer que ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 . On a ab/(1-c^2 )= ab/(〖(a+b+c)〗^2-c^2 )=ab/(a^2+b^2+2ab+2bc+2ca) . On a aussi a^2+b^2+2ab+2bc+2ca≥8〖(a^6 b^6 c^4)〗^(1/  =8a^(3/4) b^(3/4) c^(1/2) ∶IAG . ↔1/(8a^(3/4) b^(3/4) c^(1/2) )≥1/(a^2+b^2+2ab+2bc+2ca) ↔(a^(1/4) b^(1/4))/(8c^(1/2) )≥ab/(a^2+b^2+2ab+2bc+2ca) donc ab/(1-c^2 )≤(a^(1/4) b^(1/4))/(8c^(1/2) ) ,de même on a bc/(1-a^2 )≤(b^(1/4) c^(1/4))/(8a^(1/2) ) et ca/(1-b^2 )≤(c^(1/4) a^(1/4))/(8b^(1/2) ) , donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤1/8 ((a^(1/4) b^(1/4))/(8c^(1/2) )+(b^(1/4) c^(1/4))/(8a^(1/2) )+(c^(1/4) a^(1/4))/(8b^(1/2) )) ≤1/8*3〖((a^(1/4) b^(1/4))/(8c^(1/2) )*(b^(1/4) c^(1/4))/(8a^(1/2) )*(c^(1/4) a^(1/4))/(8b^(1/2) ))〗^(1/3)=3/8 ∶IAG , donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
