qlq limites

1) 


2) 

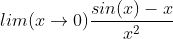Amicalment..

2) Le développement de sin x à l'ordre 3 au voisinage de 0 est : x - (x^3)/6 + O(0), donc le développement limité de sin x - x à l'ordre 3 au voisinage de 0 est : - (x^3)/6 + T(0), et donc le développement de (sin x - x)/(x^2) à l'ordre 3 au voisinage de 0 est : x/6 + S(0), 
donc lim (sin x - x)/(x^2) quand x tend vers 0 est 0.

1) Le calcul de cette limite est direct, puisque le numérateur et le dénominateur ne sont pas nuls en même temps. sauf erreur, elle est égale à -1/(rac(6)+rac(3)-1).

Oui c'est ça , mercii aymen

pour les DL tu peux me lancer le cour de ce genre des solutions ? ^^

Bien volontiers, M. Amiral.
Veuillez trouver via ce lien le cours que vous avez demandé:http://fr.wikipedia.org/wiki/D%C3%A9veloppement_limit%C3%A9
Bonne lecture.

Bonjour.
Les DL sont des outils très très simples qui permettent d'exploser presque toutes les limites en un rien de temps, mais vous ne pouvez bien sur pas les utiliser en trucs officiels, puisque c'est pas en programme au lycée. pour les curieux, je conseil ce cours de prépa 1ère année http://mp.cpgedupuydelome.fr/cours.php?id=3993 . Mais je conseille d'essayer de faire les limites par les outils dont vous disposez, sinon, avec les DL, ça n'a même plus d'intérêt de poster des limites   

Amiral a écrit:

2) 

Méthode 1
puisque on a une forme non déterminée

Pouraais-tu m'eclairer a propos du premier passage de la première methode

Aussi je ne vois pas comment tu as pus conclure le resultat dans la deuxième methode. Car je sais qu une limite ne peut etre calculé partiellement , cad remplacer sin/x par 1 dabord puis calculer 1/x-1/x
Amicalement et en attente de votre réponse ,

faute de frappe,
dérivation de (x^2)=2x mais heureusement elle ne va pas changer le résultat
pour la 2 méthode je suis complétement pas sur, parce que remplacer sin/x et puis calculer la limite du reste est pas autorisé.

la méthode 2 est complètement fausse. La méthode 1 : je ne comprend pas comment tu justifie ton premier passage.
Je propose de montrer que pour x dans [0, Pi/2], x-(x^3)/6< sin(x)< x .

Bovlmakovl a écrit:

la méthode 2 est complètement fausse. La méthode 1 : je ne comprend pas comment tu justifie ton premier passage.
Je propose de montrer que pour x dans [0, Pi/2],  x-(x^3)/6< sin(x)< x .

application du règle de l’hôpital rien que ça

d'accord. pr la première méthode c bon

Bovlmakovl a écrit:

Bonjour.
Les DL sont des outils très très simples qui permettent d'exploser presque toutes les limites en un rien de temps, mais vous ne pouvez bien sur pas les utiliser en trucs officiels, puisque c'est pas en programme au lycée. pour les curieux, je conseil ce cours de prépa 1ère année http://mp.cpgedupuydelome.fr/cours.php?id=3993 . Mais je conseille d'essayer de faire les limites par les outils dont vous disposez, sinon, avec les DL, ça n'a même plus d'intérêt de poster des limites   

Merci bov pr vos infos  

La  methode  de Mr.L.W.P est la regle de l'hopital avec f(a)=g(a)=0

non Mr. Nas8, ceci est, selon Wiki, l'énoncé simple de la règle. ce que Mr. LWP a utilisé est la première généralisation que voici : http://fr.wikipedia.org/wiki/R%C3%A8gle_de_L'H%C3%B4pital#.C3.89nonc.C3.A9_des_r.C3.A8gles_de_L.27H.C3.B4pital

sin(0) - 0 =0 et (0)² = 0

Voici un exercice limite que j'ai bien aimé :

Bien vu M. Legend_Crush: il ne manquait que la deuxième partie de la question, chose qui est totalement secondaire, vu que c'est le début du chemin qui est important.

Pour offrir de la compagnie à votre solution, voici la solution que l'auteur de l'exercice a proposé: avec bien sûr quelques petites retouches de ma part.

Voici un autre exercice:

lim x/sin(1/x)
x->0

Remarque: j'ai résolu cet exercice grâce au logiciel Wolframalpha et une indication d'un ami qui m'a aidé à chercher sur Internet pour confirmer ma solution.

Comme le but est d'ouvrir de nouveaux horizons, et comme je n'aime pas dormir en laissant derrière moi un problème non résolu, je me permet de donner la solution et de laisser quelqu'un d'autre poster un autre exercice:

La solution est: la limite n'existe pas.

En s'aidant de Wolframalpha on a:




De plus, pour pouvoir parler de la limite d'une fonction en un point, il faut que cette fonction soit définie dans un voisinage de ce point.

Pour tout h∈IR∗+, les intervalles ]−h,0[ et ]0,h[ contiennent des points de la forme 1/(n*pi) avec n∈Z. Ainsi la quantité donnée n'est définie dans aucun des ces intervalles et on ne peut donc pas parler de sa limite en 0.

C'est bien le travail que vous venez de faire, il est toujours intéressant de découvrir diverses méthodes.
Sauf que l'exo me parait bcp plus simple, il suffit de prendre la suite Xn = 1/ (2n*Pi + 1/n^2) ... elle tend bien vers 0 quand n tend vers l'infini, pourtant la limite donnée tend vers l'infini .
Mnt, on considère la suite 1/(2n*Pi + Pi/2) ... la limite proposée est 0 . donc on a deux suites qui tendent vers 0 et pour lesquels la limite donnée est différente, donc la limite n'existe pas.

Merci M. Bovlmakovl pour la méthode des "suites": vous venez de m'initier à cette méthode dont j'essaierai de faire bon usage.

Bonsoir;
Voici un exercice pour réanimer cette page et souffler un peu de vie dans son ambiance.

solution
il suffit de remarquer que


       
théorème de gendarmes