| | Limite (arctang) |  |
|
+12o0aminbe0o kalm wiles callo Alaoui.Omar JASPER youness boye Ayak omis clever007 $arah Nea® 16 participants |
|
| Auteur | Message |
|---|
Nea®
Expert sup

 Nombre de messages : 686 Nombre de messages : 686
Age : 34
Localisation : Marrakech
Date d'inscription : 29/10/2007
 |  Sujet: Limite (arctang) Sujet: Limite (arctang)  Mar 27 Nov 2007, 22:14 Mar 27 Nov 2007, 22:14 | |
| | |
|
  | |
$arah
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 33
Localisation : marrakech
Date d'inscription : 13/08/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mar 27 Nov 2007, 22:21 Mar 27 Nov 2007, 22:21 | |
| on a x-xouss3 inf arctan x inf x
et c est fait | |
|
  | |
Nea®
Expert sup

 Nombre de messages : 686 Nombre de messages : 686
Age : 34
Localisation : Marrakech
Date d'inscription : 29/10/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mar 27 Nov 2007, 22:40 Mar 27 Nov 2007, 22:40 | |
| | |
|
  | |
clever007
Maître

 Nombre de messages : 98 Nombre de messages : 98
Age : 33
Localisation : Marrakech
Date d'inscription : 18/11/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mar 27 Nov 2007, 23:13 Mar 27 Nov 2007, 23:13 | |
| | |
|
  | |
omis
Expert grade2

 Nombre de messages : 333 Nombre de messages : 333
Age : 33
Date d'inscription : 25/03/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 11:48 Mer 28 Nov 2007, 11:48 | |
| 0  | |
|
  | |
Ayak
Maître

 Nombre de messages : 87 Nombre de messages : 87
Age : 35
Date d'inscription : 19/11/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 12:04 Mer 28 Nov 2007, 12:04 | |
| c troo facile brother mé merci kan meme ca fé bougé | |
|
  | |
youness boye
Maître

 Nombre de messages : 181 Nombre de messages : 181
Age : 34
Localisation : marrakech
Date d'inscription : 17/11/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 12:24 Mer 28 Nov 2007, 12:24 | |
| c'est trés facile  lim [arctan (x)-x] / x² = [ arctan (x) / x²] - [ x/x²] = [ arctan (x) / x * 1/x ] - [1/x] on a [ arctan (x) / x ] = 1 = 1 * 1/x - 1/x =0  | |
|
  | |
JASPER
Maître

 Nombre de messages : 100 Nombre de messages : 100
Age : 34
Localisation : La banquise
Date d'inscription : 13/06/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 12:43 Mer 28 Nov 2007, 12:43 | |
| - youness boye a écrit:
c'est trés facile  lim [arctan (x)-x] / x² = [ arctan (x) / x²] - [ x/x²] = [ arctan (x) / x * 1/x ] - [1/x] on a [ arctan (x) / x ] = 1 = 1 * 1/x - 1/x =0  comment ? ce n'est pas juste  il y a une seule méthode c'est l'encadrement !! | |
|
  | |
Nea®
Expert sup

 Nombre de messages : 686 Nombre de messages : 686
Age : 34
Localisation : Marrakech
Date d'inscription : 29/10/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 13:05 Mer 28 Nov 2007, 13:05 | |
| - youness boye a écrit:
c'est trés facile  lim [arctan (x)-x] / x² = [ arctan (x) / x²] - [ x/x²] = [ arctan (x) / x * 1/x ] - [1/x] on a [ arctan (x) / x ] = 1 = 1 * 1/x - 1/x =0  C faux  | |
|
  | |
clever007
Maître

 Nombre de messages : 98 Nombre de messages : 98
Age : 33
Localisation : Marrakech
Date d'inscription : 18/11/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 13:05 Mer 28 Nov 2007, 13:05 | |
| Oui ; une seule méthode c'est l'encadrement !
Quand t'as [ arctan (x) / x * 1/x ] - [1/x]
Soi tu remplace le tout par Zéro soi tu laisse tout !
La seule méthode c'est que :
x-x^3 #plu pti ke # Arctan(x) #plu pti ke# x
C'est facile de le démontrer puis le reste c'est banal !
A+ | |
|
  | |
youness boye
Maître

 Nombre de messages : 181 Nombre de messages : 181
Age : 34
Localisation : marrakech
Date d'inscription : 17/11/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 13:22 Mer 28 Nov 2007, 13:22 | |
| merci les amis
mais je ve connaitre
pourquoi est faux ??
j'ai utiliser
arctan (x) / x = 1 | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 13:37 Mer 28 Nov 2007, 13:37 | |
| - clever007 a écrit:
- Oui ; une seule méthode c'est l'encadrement !
Quand t'as [ arctan (x) / x * 1/x ] - [1/x]
Soi tu remplace le tout par Zéro soi tu laisse tout !
La seule méthode c'est que :
x-x^3 #plu pti ke # Arctan(x) #plu pti ke# x
C'est facile de le démontrer puis le reste c'est banal !
A+ Salut Ami  Je suis Pas Avec toi ! y en a plusieurs méthodes Plus Facile que l'encadrement! a titre D'exemple L'hôpital . A+ | |
|
  | |
youness boye
Maître

 Nombre de messages : 181 Nombre de messages : 181
Age : 34
Localisation : marrakech
Date d'inscription : 17/11/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 13:43 Mer 28 Nov 2007, 13:43 | |
| oui mon frére
il ya plusieures de méthode pour le résoudre | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 13:48 Mer 28 Nov 2007, 13:48 | |
| C'est ça: 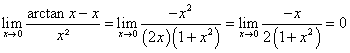 | |
|
  | |
clever007
Maître

 Nombre de messages : 98 Nombre de messages : 98
Age : 33
Localisation : Marrakech
Date d'inscription : 18/11/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 17:57 Mer 28 Nov 2007, 17:57 | |
| Explique un p'ti peu stp cher ami Omar !
A+ | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 19:05 Mer 28 Nov 2007, 19:05 | |
| SalutTu Peut Lire ça : - Citation :
- Énoncé des règles de L'Hôpital
Première généralisation à des fonctions pour lesquelles  n'existe pas forcément. Si f et g sont deux fonctions dérivables sur ] a ; b[ dont la limite en a est nulle, si g'(x) ne s'annule pas sur ]a ; b[ et si  alors  . Le résultat est valide que L soit une limite réelle ou infinie. Ou bien Visite cette Page :http://fr.wikipedia.org/wiki/R%C3%A8gle_de_L'H%C3%B4pital A+ | |
|
  | |
clever007
Maître

 Nombre de messages : 98 Nombre de messages : 98
Age : 33
Localisation : Marrakech
Date d'inscription : 18/11/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 19:18 Mer 28 Nov 2007, 19:18 | |
| Ah !
C'est la 1ère fois que je vois ça moi !
Mais est ce que ces règles " de l'hopital " comme t'as dit sont dans notre manuel de maths !
Si ce n'est pas le cas je ne crois pas que cette méthode sera accéptée au Terminal !
A+ | |
|
  | |
callo
Expert sup

 Nombre de messages : 1481 Nombre de messages : 1481
Age : 34
Localisation : paris
Date d'inscription : 03/03/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 19:39 Mer 28 Nov 2007, 19:39 | |
| cette règle est hors programme, mais elle sert toutefois à verifier quelques limites difficiles.
Dernière édition par le Mer 28 Nov 2007, 19:40, édité 1 fois | |
|
  | |
wiles
Expert sup

Nombre de messages : 501
Age : 34
Localisation : khouribga
Date d'inscription : 03/04/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 19:39 Mer 28 Nov 2007, 19:39 | |
| l'hopital est hors-programme mais demontrable par des outils terminal a savoir le 'TAF'
a+ | |
|
  | |
clever007
Maître

 Nombre de messages : 98 Nombre de messages : 98
Age : 33
Localisation : Marrakech
Date d'inscription : 18/11/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Mer 28 Nov 2007, 19:44 Mer 28 Nov 2007, 19:44 | |
| Meerci pour l'info !
C'est à dire que le seul moyen que l'on peut utiliser et qui est en programme ; l'encadrement !
A+ | |
|
  | |
youness boye
Maître

 Nombre de messages : 181 Nombre de messages : 181
Age : 34
Localisation : marrakech
Date d'inscription : 17/11/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Jeu 29 Nov 2007, 10:46 Jeu 29 Nov 2007, 10:46 | |
| | |
|
  | |
JASPER
Maître

 Nombre de messages : 100 Nombre de messages : 100
Age : 34
Localisation : La banquise
Date d'inscription : 13/06/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Jeu 29 Nov 2007, 11:26 Jeu 29 Nov 2007, 11:26 | |
| - youness boye a écrit:
- arctan (x) / x = 1
quoi ? ce que tu as mis au début est banal comme l'a dit clever !! | |
|
  | |
omis
Expert grade2

 Nombre de messages : 333 Nombre de messages : 333
Age : 33
Date d'inscription : 25/03/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Jeu 29 Nov 2007, 12:08 Jeu 29 Nov 2007, 12:08 | |
| - JASPER a écrit:
- youness boye a écrit:
- arctan (x) / x = 1
quoi ? ce que tu as mis au début est banal comme l'a dit clever !! on a limx->0[arctan (x) / x] = 1 ce ke tu as ecrit et faux .... a+ Omis | |
|
  | |
kalm
Expert sup

Nombre de messages : 1101
Localisation : khiam 2
Date d'inscription : 26/05/2006
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Jeu 29 Nov 2007, 12:37 Jeu 29 Nov 2007, 12:37 | |
| on peut facilement montrer que x-x^3/3=<actanx=<x-x^3/3+x^5/5 tel que x de IR+
donc -x/3 =< (actanx-x)/x² =<-x/3+x^3/5
d'ou la limite est 0 | |
|
  | |
o0aminbe0o
Expert sup
 Nombre de messages : 963 Nombre de messages : 963
Age : 34
Date d'inscription : 20/05/2007
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  Jeu 29 Nov 2007, 12:38 Jeu 29 Nov 2007, 12:38 | |
| voila  http://fr.wikipedia.org/wiki/R%C3%A8gle_de_L'H%C3%B4pital | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Limite (arctang) Sujet: Re: Limite (arctang)  | |
| |
|
  | |
| | Limite (arctang) |  |
|
