| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 05:17 Jeu 19 Nov 2009, 05:17 | |
| - rachid18 a écrit:
- nmo a écrit:
- x,y,z,t étant des réels tels que x>=-1, y>=-1, z>=-1, t>=-1.
et x+y+z+t=2.
démontrez que: x^3+y^3+z^3+t^3>=1/2.
Malheureusement,toutes les solutions présentées sont fausses,puisque l'application de l'inégalité de Holder ou Caushy-Schwartz n'est pas autorisée pour les réels négatifs.En effet,j'ai dèja rencontré l'inégalité ça fait à peu près 2 ans et j'ai dèja posté ma solution sur ce forum.La solution était ainsi :
- rachid18 a écrit:
- Posons :
x=a-1 , y=b-1 , z=c-1 et t=d-1
L'inégalité devient :
a^3 +b^3 +c^3 +d^3 -3(a²+b²+c²+d²) +27/2 > 0 avec a,b,c,d >= 0 et a+b+c+d=6,
On a :
a^3 +b^3 +c^3 +d^3 >= (a²+b²+c²+d²)²/(a+b+c+d) = (a²+b²+c²+d²)²/6 ( Caushy-Shwartz );
Il suffit de prouver que:
(a²+b²+c²+d²)²/6 -3(a²+b²+c²+d²) +27/2 > 0;
Ce qui est équivalent à :
(a²+b²+c²+d²-9)² > 0 ce qui est vrai. bsr ... JE vois pas d'ou tu tire sa moi j'ai toujours cru que cauchy shwarz s'appliquait a tout les réels et je pense que c'est le cas pour Holder aussi ... eceque tu pourrait donner un contre exemple stp | |
|
  | |
rachid18
Expert grade2

 Nombre de messages : 369 Nombre de messages : 369
Age : 32
Date d'inscription : 23/03/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 14:54 Jeu 19 Nov 2009, 14:54 | |
| - darkpseudo a écrit:
- bsr ...
JE vois pas d'ou tu tire sa moi j'ai toujours cru que cauchy shwarz s'appliquait a tout les réels et je pense que c'est le cas pour Holder aussi
... eceque tu pourrait donner un contre exemple stp Bonjour, Malheureusement,tu avais tort.Bon,on sait que si x,y,z >= 0,selon l'inégalité de Caushy-Shwartz : (x^3+y^3+z^3)(x+y+z) >= (x²+y²+z²)² Cela n'est pas vrai pour tous les réels négatifs x,y et z.Contre exemple : prendre x=-y ! ... | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 21:59 Jeu 19 Nov 2009, 21:59 | |
| a,b,c,d sont des nombres réels
montrez que
2(a^3+b^3+c^3)>=ab(a+b)+(b+c)bc+(c+a)ac
montrez oci que
(a^2+b^2^)c+(b^2+c^2)a+(c^2+a^2)b>=6abc | |
|
  | |
samix
Expert grade2

 Nombre de messages : 322 Nombre de messages : 322
Age : 30
Localisation : Oujda
Date d'inscription : 02/12/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 22:04 Jeu 19 Nov 2009, 22:04 | |
| - naplhitl a écrit:
- a,b,c,d sont des nombres réels
montrez que
2(a^3+b^3+c^3)>=ab(a+b)+(b+c)bc+(c+a)ac
montrez oci que
(a^2+b^2^)c+(b^2+c^2)a+(c^2+a^2)b>=6abc 1) a²+b²>=2ab a²+b²-ab>=ab (a+b)(a²+b²-ab)>=ab(a+b) a^3+b^3>=ab(a+b) b^3+c^3>=bc(b+c) c^3+a^3>=ac(a+c) Somme : 2(a^3+b^3+c^3)>=ab(a+b)+bc(b+c)+ac(a+c) 2) a²+b²>=2ab c(a²+b²)>=2abc b(c²+a²)>=2abc a(b²+c²)>=2abc somme : a(b²+c²)+c(a²+b²)+b(c²+a²)>=6abc | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 22:33 Jeu 19 Nov 2009, 22:33 | |
| | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 22:35 Jeu 19 Nov 2009, 22:35 | |
| x appartient à l'intervalle ouvert 1,2
montrez que
-3<2x^2-3x-2<0
Dernière édition par naplhitl le Jeu 19 Nov 2009, 22:42, édité 1 fois | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 22:40 Jeu 19 Nov 2009, 22:40 | |
| svp pouvez vous postez la réponse de exo2. | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 22:43 Jeu 19 Nov 2009, 22:43 | |
| | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 22:45 Jeu 19 Nov 2009, 22:45 | |
| lexo k j vien d poser il est simple c juste pr éditer un ote msg k j lai écrit cherchez mm po la solution | |
|
  | |
yumi
Maître

 Nombre de messages : 156 Nombre de messages : 156
Age : 30
Localisation : {Univers des éventualités}U/{My Land}
Date d'inscription : 08/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 23:23 Jeu 19 Nov 2009, 23:23 | |
| nn le voici;
soit xet y de nombres reels tel que: 1≤x²-xy+x²≤2
1/ montrez que : 2/9≤x^4+y^4≤8
2/montrez que pour tout n de N tel que n≥3; on a :
x^2n+y^2n≥2/3^2n
svp aidez moi. | |
|
  | |
fatima agorram
Débutant
 Nombre de messages : 3 Nombre de messages : 3
Age : 24
Date d'inscription : 19/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 19 Nov 2009, 23:24 Jeu 19 Nov 2009, 23:24 | |
| salut à tout l monde.
[i][b][b]j suis tellement perturbé .ou est la réponse correcte maintenant?
et merci d'avance | |
|
  | |
naplhitl
Féru
 Nombre de messages : 61 Nombre de messages : 61
Age : 29
Date d'inscription : 16/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 20 Nov 2009, 07:40 Ven 20 Nov 2009, 07:40 | |
| n est entier naturel non nul?
montrez que
2(racine carréede(n+1)-racine carrée den)<1/racine carrée de n<2(racine carrée de n-racine carrée de n-1
on pose(racine carrée c le signe$
A=1/$1+1/$2+1/$3.......+1/$10000
montrez que
2($1001-1)<A<199 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 20 Nov 2009, 15:09 Ven 20 Nov 2009, 15:09 | |
| La solution de cet exercice est en bas.
Dernière édition par nmo le Dim 20 Juin 2010, 17:42, édité 2 fois (Raison : solution incompréhensible) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 20 Nov 2009, 15:23 Ven 20 Nov 2009, 15:23 | |
| Un nouvel exercice: Soit a,b et c des nombres strictement positifs: Démontrez que 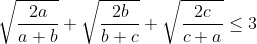 . Merci d'avance pour les réponses. Bonne chance.
Dernière édition par nmo le Ven 28 Jan 2011, 14:44, édité 4 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 21 Nov 2009, 11:22 Sam 21 Nov 2009, 11:22 | |
| Démontez que:
* 8+8²..........................8^888=73k /k appartient à l'ensemble N.
* 5+5²+5^3........................5^555=31k /k appartient à l'ensemble N.
Bonne chance.
Dernière édition par nmo le Dim 20 Juin 2010, 17:44, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 21 Nov 2009, 11:37 Sam 21 Nov 2009, 11:37 | |
| La solution que j'ai présenté semble incompréhensible pour l'exercice de naplhitl c'est pour ça que j'ai éditer mes messages.
Dernière édition par nmo le Dim 20 Juin 2010, 17:43, édité 2 fois (Raison : la même raison que la première) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 21 Nov 2009, 11:38 Sam 21 Nov 2009, 11:38 | |
| Voilà la solution pour le problème de début: - houssam110 a écrit:
- x²+y²=<2+xy
x^4+y^4+2x²y²=<4+x²y²+4xy
<=>x^4+y^4=<4xy+4-x²y²
<=>x^4+y^4-8=<-x²y²+4xy-4=-(xy-2)²=<0
<=>x^4+y^4=<8 (1)
on sait que 1/2(x²+y²)>=-xy
<=> 3/2(x²+y²)>=x²-xy+y²>=1
<=>x²+y²>=2/3
il est très facile de prouver que x^4+y^4>=1/2(x²+y²)²
donc x^4+y^4 >=1/2*4/9=2/9 (2)
de (1) et (2) ....
j'attends la confirmation.
Dernière édition par nmo le Sam 19 Juin 2010, 11:33, édité 1 fois | |
|
  | |
issam erriahi
Expert sup

 Nombre de messages : 1102 Nombre de messages : 1102
Age : 34
Date d'inscription : 31/12/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 22 Nov 2009, 11:20 Dim 22 Nov 2009, 11:20 | |
| bien jouis nmo t'as raison | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 22 Nov 2009, 15:29 Dim 22 Nov 2009, 15:29 | |
| Mais il reste celui ci:
Montrez que pour tout n de N tel que n≥3; on a :
x^(2n)+y^(2n)≥2/3^(2n).
Et je pense qu'on peut la déduire des question précédante.
Au plaisir.
Dernière édition par nmo le Ven 28 Jan 2011, 14:45, édité 3 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 22 Nov 2009, 17:35 Dim 22 Nov 2009, 17:35 | |
| - rachid18 a écrit:
- darkpseudo a écrit:
- bsr ...
JE vois pas d'ou tu tire sa moi j'ai toujours cru que cauchy shwarz s'appliquait a tout les réels et je pense que c'est le cas pour Holder aussi
... eceque tu pourrait donner un contre exemple stp Bonjour,
Malheureusement,tu avais tort.Bon,on sait que si x,y,z >= 0,selon l'inégalité de Caushy-Shwartz :
(x^3+y^3+z^3)(x+y+z) >= (x²+y²+z²)²
Cela n'est pas vrai pour tous les réels négatifs x,y et z.Contre exemple : prendre x=-y ! ... bjr ... Heu si on prend ton égaliter elle doit s'écrir sous la forme : ((xVx)^2+(yVy)^2+(zVz)^2)(x+y+z) >= (x²+y²+z²)² pour pouvoir appliquer Caushy ... or si on prend un réel négatif avec la racine on sera dans les nombres complexes ( dont je ne connais pas grand chose ) ; donc voila ma question dans ton contre-exemple il y a une racine négative ... eceque tu pourrait donner un exemple sans racine négative ... Dsl d'être aussi casse pieds !! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 26 Nov 2009, 16:19 Jeu 26 Nov 2009, 16:19 | |
| a, b, et c sont des nombres positifs tels que a<b+c
Montrez que a/(1+a)<b/(1+b)+c/(1+c).
Bonne chance.
Dernière édition par nmo le Mar 18 Mai 2010, 21:26, édité 1 fois | |
|
  | |
yassine-516
Maître

 Nombre de messages : 128 Nombre de messages : 128
Age : 31
Date d'inscription : 11/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 26 Nov 2009, 16:35 Jeu 26 Nov 2009, 16:35 | |
| je pense k il ya comme cet exo ds dimadima 1 er sc math | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 27 Nov 2009, 10:13 Ven 27 Nov 2009, 10:13 | |
| Comme je n'ai pas ce dimadima je veux savoir la solution.
Merci d'avance.
Dernière édition par nmo le Dim 20 Juin 2010, 17:47, édité 1 fois | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 27 Nov 2009, 10:29 Ven 27 Nov 2009, 10:29 | |
| y a la solution avec les fonctions(belle et courte)
tu considère la fonction x/(x+1) qui est croissante sur l'intervalle [0,+00[
on a a<b+c <=>a+1<b+c+1
alors en appliquant x/(x+1)
on aura:a/(1+a)<(b+c)/(1+b+c)=b/(1+b+c)+c/(1+b+c)<b/(1+b)+c/(1+c)
-------------------------------------------------------------------------
et puis la solution du calcul:(moche et ennuyeuse)
on sait que a<b+c<=>a+ac+ab<b+c+ac+ab<=>a+ac+ab+abc<b+c+ac+ab+2abc+2bc
<=>a(1+c+b+bc)<(b+c+2bc)(1+a)
<=>a(1+c)(1+b)<(b(c+1)+c(b+1))(1+a)
<=>a/(1+a)<b/(1+b)+c/(1+c)
Dernière édition par majdouline le Sam 28 Nov 2009, 20:33, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 27 Nov 2009, 11:32 Ven 27 Nov 2009, 11:32 | |
| N'y a t il pas une solution du calcul plus belle que celle ci et sans utilisation de cette ligne: a+ac+ab+abc<b+c+ac+ab+2abc+2bc?
Merci pour la réponse.
Dernière édition par nmo le Dim 20 Juin 2010, 17:47, édité 2 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
