| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 28 Avr 2010, 18:20 Mer 28 Avr 2010, 18:20 | |
| Soit a,b,c Dans QI : Montrer que si : ab+ac+bc=1 alors : 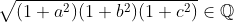 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 28 Avr 2010, 18:37 Mer 28 Avr 2010, 18:37 | |
| Bon voici la réponse: On a 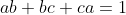 . Donc ^2=1^2) . Donc ^2+(bc)^2+(ca)^2+2abc(a+b+c)=1) après la simplification. Donc ^2+(bc)^2+(ca)^2=1-2abc(a+b+c)) . D'autre part, on a (1+b^2)(1+c^2)}=\sqrt{1+a^2+b^2+c^2+(ab)^2+(bc)^2+(ca)^2+(abc)^2}) après la simplification. Donc (1+b^2)(1+c^2)}=\sqrt{1+a^2+b^2+c^2+1-2abc(a+b+c)+(abc)^2}) . Donc (1+b^2)(1+c^2)}=\sqrt{2+a^2+b^2+c^2-2abc(a+b+c)+(abc)^2}) . Donc (1+b^2)(1+c^2)}=\sqrt{2(ab+bc+ca)+a^2+b^2+c^2-2abc(a+b+c)+(abc)^2}) . Donc (1+b^2)(1+c^2)}=\sqrt{(a+b+c)^2-2abc(a+b+c)+(abc)^2}) . Donc (1+b^2)(1+c^2)}=\sqrt{(a+b+c-abc)^2}) . Donc (1+b^2)(1+c^2)}=|a+b+c-abc|) . Ce qui affirme que (1+b^2)(1+c^2)}) est un élément de QI. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 28 Avr 2010, 18:40 Mer 28 Avr 2010, 18:40 | |
| Oué Bonne réponse ! A toi !  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 28 Avr 2010, 18:56 Mer 28 Avr 2010, 18:56 | |
| L'exercice est le suivant:
Soient a, b et c trois réels tels que: |a|<1, |b|<1, et |c|<1.
Montrer que ab+cb+ca+1>0.
Bonne chance. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 28 Avr 2010, 19:25 Mer 28 Avr 2010, 19:25 | |
| Posons : 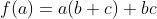 f est une fonction affine , alors on va s'intéresser à deux cas ,puisque si b+c=0 l'inégalité est trivial .. Cas 1 : b+c>0 Puisque f est affine On a donc : 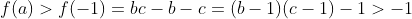 Cas 2 : Cas 2 :b+c<0 Puisque f est affine on a : 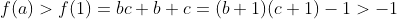 D'où le résultat . En effet on peut prouver de la même façons que |ab+ac+bc|<1 Exo Suivant :Trouvez tous les entiers naturels a,b,c t.q : a+b+c=abc | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 08:25 Jeu 29 Avr 2010, 08:25 | |
| slt , je veux s'inscrire dans votres jeux ! alors je poste ma reponse ^^:
on peut supposer a=<b<=c :
donc on a a+b+c =< 3c ==> abc =<3c ==> ab=<3
donc il vient que ab=0 ou ab=1 ou ab=2 ou ab=3
alors ab=0 ==> a=b=0 ==> c=0
ab=1 ==>a=b=1 ==> 2+c=c (contradiction )
ab=2 ==> b=2 et a=1 (a=<b) ==> c=3
ab=3 ==> b=3 et a=1 ==> c=2 .
d'ou la conclusion de S ^^ .
alors? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 08:34 Jeu 29 Avr 2010, 08:34 | |
| - master a écrit:
- slt , je veux s'inscrire dans votres jeux ! alors je poste ma reponse ^^:
on peut supposer a=<b<=c :
donc on a a+b+c =< 3c ==> abc =<3c ==> ab=<3
donc il vient que ab=0 ou ab=1 ou ab=2 ou ab=3
alors ab=0 ==> a=b=0 ==> c=0
ab=1 ==>a=b=1 ==> 2+c=c (contradiction )
ab=2 ==> b=2 et a=1 (a=<b) ==> c=3
ab=3 ==> b=3 et a=1 ==> c=2 .
d'ou la conclusion de S ^^ .
alors? On conclut que les triplets de solutions sont (0,0,0), (1,2,3), (2,1,3),(1,3,2), (2,3,1), (3,2,1), et (3,1,2). Bon travail. C'est à toi de poster le prochain exercice. | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 08:58 Jeu 29 Avr 2010, 08:58 | |
| merci nmo ^^ : alors !  avec (x,y)£R | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 09:09 Jeu 29 Avr 2010, 09:09 | |
| - master a écrit:
- merci nmo ^^ : alors !

avec (x,y)£R Je pense qu'il manque quelque chose. Sinon l'equation admet une infinité de solution. | |
|
  | |
Arithmysis
Débutant
 Nombre de messages : 8 Nombre de messages : 8
Age : 29
Date d'inscription : 25/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 09:53 Jeu 29 Avr 2010, 09:53 | |
| Bonjour,
Je crois qu'il s'agit de preciser la forme Generale des Solutions . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 10:12 Jeu 29 Avr 2010, 10:12 | |
| La réponse est ainsi: Le domaine de définition est x et y doivent être positifs. On a 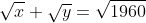 . Donc 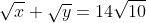 . Donc 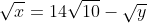 . Donc ^2=(14\sqrt{10}-\sqrt{y})^2) . Donc 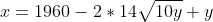 . Donc 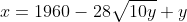 . Donc l'ensemble des solution s'éecrit de la forme (1960-28V(10y)+y,y) tel que y est un réel positif.
Dernière édition par nmo le Jeu 29 Avr 2010, 14:33, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 10:16 Jeu 29 Avr 2010, 10:16 | |
| Voic un exercice de défi de l'année passée: a et b sont deux réels vérifiant ^{2006}) . Calculez 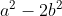 . Bonne chance. | |
|
  | |
Arithmysis
Débutant
 Nombre de messages : 8 Nombre de messages : 8
Age : 29
Date d'inscription : 25/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 11:08 Jeu 29 Avr 2010, 11:08 | |
| Pour l'equation du Master !  Puisque : 1960-y+x £ Z Alors V10x £ Q Donc : 10x=m^2 , m £ IN Ce qui implique : 10 / m Donc m=10k , k £ IN Ce qui donne : x=10k^2 . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 11:34 Jeu 29 Avr 2010, 11:34 | |
| - Arithmysis a écrit:
- Pour l'equation du Master !

Puisque : 1960-y+x £ Z Alors V10x £ Q
Donc : 10x=m^2 , m £ IN
Ce qui implique : 10 / m Donc m=10k , k £ IN
Ce qui donne : x=10k^2 . Je pense que master demande la solution en IR, ni en IZ, ni en QI. Amicalement. | |
|
  | |
Arithmysis
Débutant
 Nombre de messages : 8 Nombre de messages : 8
Age : 29
Date d'inscription : 25/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 11:49 Jeu 29 Avr 2010, 11:49 | |
| Ce qui est dans l'enoncé est que x,y £ IR .. La Solution trouver verefie l'equation ... l'utilisation de QI & IZ n'es que pour arriver au resultat le plus simplifier ...
Bon nous attendons alors l'avis de Master . | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 12:44 Jeu 29 Avr 2010, 12:44 | |
| slt , re^^ :
@ arithmysis : t'a dis que 1960-y+x £Z ,dsl je crois que c'est faux .c plutot R car (x,y)£R donc ce qui ne prouve pas ce que ta dis !! essay autre fois
@ nmo : je crois que ta soluc est vrais ! a toi ^^ | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 12:56 Jeu 29 Avr 2010, 12:56 | |
| - master a écrit:
- slt , re^^ :
@ arithmysis : t'a dis que 1960-y+x £Z ,dsl je crois que c'est faux .c plutot R car (x,y)£R donc ce qui ne prouve pas ce que ta dis !! essay autre fois
@ nmo : je crois que ta soluc est vrais ! a toi ^^ C'est ça ce que je voulais lui dire mais j'ai hésité. Voici mon exercice: - nmo a écrit:
- Voic un exercice de défi de l'année passée:
a et b sont deux réels vérifiant ^{2006}) . .
Calculez 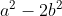 . .
Bonne chance. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 14:26 Jeu 29 Avr 2010, 14:26 | |
| [quote=\"nmo\"]Voic un exercice de défi de l\'année passée: a et b sont deux réels vérifiant ^{2006}) . Calculez 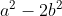 . Bonne chance.[/quote] Bonjour, revenue  Regarde[DowN] J\'éspére que je n\'ai fais un faute d\'innatention.
Dernière édition par M.Marjani le Jeu 29 Avr 2010, 14:39, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 14:29 Jeu 29 Avr 2010, 14:29 | |
|
Dernière édition par M.Marjani le Ven 30 Avr 2010, 11:16, édité 2 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 14:38 Jeu 29 Avr 2010, 14:38 | |
| - M.Marjani a écrit:
- nmo a écrit:
- Voic un exercice de défi de l'année passée:
a et b sont deux réels vérifiant ^{2006}) . .
Calculez 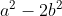 . .
Bonne chance.
Bonjour, revenue 
On a: a²-2b²=(a+bV2)(a-bV2) (1)
Et (a+bV2)(a+bV2)=(1+V2)^4012 (2)
(1)/(2) donne: (a-bV2)/(a+bV2)=(a²-2b²)/(1+V2)^4012
Posons: x=a,y=bV2 et (1+V2)^4012=K
Nous avons: (x-y)/(x+y)=(x²-y²)/K
=> (x-y)/Vk=(x²-y²)/k
=> Vk(x-y)=x²-y² , ce qui est clair: Vk=x=y
=> a²-2b²=0
J'éspére que je n'ai fais un faute d'innatention. Cela veut dire Vk(x-y)=(x-y)(x+y). Donc (x-y)(Vk-x-y)=0. Donc x-y=0 ou Vk-x-y=0. Donc x=y ou Vk=x+y (ce qui est juste d'après l'énoncé). De ce point, on ne peut pas dire que x=y que si Vk#x+y. Ce qui est faux. Amicalement. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 29 Avr 2010, 20:21 Jeu 29 Avr 2010, 20:21 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 30 Avr 2010, 19:18 Ven 30 Avr 2010, 19:18 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 30 Avr 2010, 20:03 Ven 30 Avr 2010, 20:03 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 30 Avr 2010, 20:08 Ven 30 Avr 2010, 20:08 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 30 Avr 2010, 20:20 Ven 30 Avr 2010, 20:20 | |
| Regarde bien la troisiéme ligne:
kx-ky=k²-2yk <=> -ky+kx=k²-2yk
La premiére cas: k=x=y on a prouver qui est faux.
donc il reste que: -y=k et x=-2y.
Comme si t'as une polynome, si tu veux voir combien vaut a et b et c.. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
