amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 01 Mai 2011, 21:44 Dim 01 Mai 2011, 21:44 | |
| good mai c fau matatkhrjch 5/4 sinon methode juste
jpasse un autre ex:
(x-1)f(x+1)-(x+2)f(x)=0
on a f(2)=6
calculf(5/2)
Mehdi jvoudrais savoir si tu es en tron commun ou sm1 car tu travaille avec des methode 6eme | |
|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 02 Mai 2011, 17:33 Lun 02 Mai 2011, 17:33 | |
| Salut amigo-6: Pour la deuxième valeur de -5/4, j'ai indiqué en haut qu'on peut l'enlever. Pour ce qui est de mon niveau  , je suis en première SM, c'est juste que je suis un peu jeune par rapport à mon âge...  Tu aurais pu le constater car je passe des olympiades de première ! | |
|
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 21 Déc 2011, 23:14 Mer 21 Déc 2011, 23:14 | |
| - samix a écrit:
  Notons un point E tel que (AO) _|_(DE) et F point d'intersection de (CO) et (BD) et O le centre du cercle circonscrit. i)Montrons que <AOB=90°AOB=2ACB=2(45°-x)=90-2x COB=2CAB=2x AOB=AOB+COB = 90° ii) Montrons <BOC=60°On a <AOB=90° donc DAE =45° et on a (AO) _|_(DE) donc ADE=45° D'où (DE)_|_ (AO) et (DF)//(AO) et (BF)_|_(CO) D'après Thales : CF=FO D'où BOC est un triangle isocele en B d'où BOC est un triangle équilatéral ( car OC=OB) Donc <BOC=60° Conclusion : x= <BAC = (<BOC)/2=60°/2=30° Sauf erreur | |
|
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 09 Avr 2012, 22:50 Lun 09 Avr 2012, 22:50 | |
| - nmo a écrit:
- Dijkschneier a écrit:
- Avec un peu de retard, mais elle est là quand même :
Solution au problème :
ADN et ADC sont semblables, et ADM et ABD sont de même semblables.
Donc : 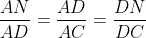 et et 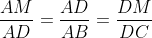 (1) (1)
On en déduit en particulier que AD²=AN.AC et AD²=AM.AB.
Donc : AD^4 = AB.AC.AN.AM
Il reste donc à montrer que AN.AM = AD.AP.
ABC étant un triangle, on a A+B+C=180 en tant qu'angles.
De fait, MDN+A=180, et par suite, le quadrilatère ANDM est inscriptible.
D'après le théorème de Ptolémée appliqué sur ce quadrilatère, on a AD.MN=AN.MD+AM.ND
Mais d'après (1), on a : 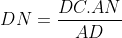 et et 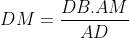
Donc, en continuant sur Ptolémée, on a : }{AD}(DB+DC)%20=%20\frac{AM.AN.BC}{AD})
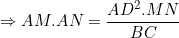 . .
Il reste donc à montrer que 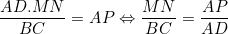 . .
Maintenant, ANM et ABC sont semblables. Par suite, 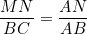 . .
Et APN et ABD sont semblables. Par suite, 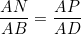 . .
Par conséquent, 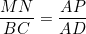 . CQFD. . CQFD. Très bien, une solution exellente, voire élégante. Je pense qu'on peut changer tout le passage de Ptolémé par: "AMP et ADN sont semblables d'où AM/AD=AP/AN d'où AN.AM = AD.AP" pour que la solution soit bien élégante.. | |
|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 23 Fév 2013, 23:56 Sam 23 Fév 2013, 23:56 | |
| - legend-crush a écrit:
- nmo a écrit:
- Inutile d'enterrer ce sujet, voici un exercice, amusez vous à le faire:
Résolvez aussi en IN² ce système:
\begin{cases}x^2-y^2=7344\\PGCD(x,y)=12\end{cases}) . .
Bonne chance.  salut ne pas oublier que 51=17*3 donc il ya encore 2 autres cas à étudier | |
|
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 24 Fév 2013, 13:25 Dim 24 Fév 2013, 13:25 | |
| ah oui, j'ai pas fait attention merci | |
|
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
