| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 13 Sep 2010, 17:23 Lun 13 Sep 2010, 17:23 | |
| - nmo a écrit:
- M.Marjani a écrit:
- @nmo: Oui, c'est vrai, la derniére phase est erroné. Mais il y avait une error dans l'énoncé, (x,y,z) sont supposé strictement positives.. Contre exemple: prendre x=y=0 et z=3. Ce qui est n'est pas définie. Ou bien, il faut dire qu'au plus l'un des variables est nulle ^^
Je reprend:
Je voullais juste utiliser des theorémes connus pour s'habituer, et pour leur utilités de ce sujet.. Sinon je peux procéder comme suit:
Solution:
* x+y+z=3 => 2(xy+yz+xz)=9-(x²+y²+z²) , on sait par IAG que: x²+y²+z² >= xy+yz+xz d'ou 2(xy+yz+xz)+xy+yz+xz =< 9 Alors on a: xy+yz+xz =< 3.
* Maintenant j'ai remarqué qu'il suffit de démontrer que: 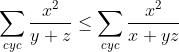 (1) (1)
* On a: 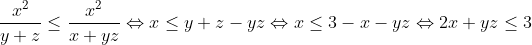
* Alors en emplyant le sigma cyclic, on aura: +xy+yz+xz\leq 9) Ce qui est vrai car Ce qui est vrai car 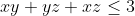
* Par l'AM-HM (Qui est un cas particulier de C.S et prouvable par AM-GM) et en posant:
 et et  et et  et et  et et  et et 
On aura cette inégalité qui est connu: ( \:2(x+y+z)\: ) \:\geq \: (x+y+z)^2)
Donc: 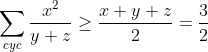
(1) Permet de dire que =\frac{3}{2}) Atteint pour Atteint pour 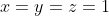
CQFD.. Tu n'a pas bien démontré la relation (1).
Je vais présenter une autre methode maintenant. A ton avis pourquoi je n'ai pas démontrer bien la relation (1) ? Pour que tu me comprends bien, nmo: Sigma = la somme des nombres. Alors que j'ai fais la somme de chaque deux nombres, l'un appratient au premier Sigma, et le deuxiéme apartient au deuxiéme, alors la somme de ces trois inégalités qu'on aura aprés simplification représente la relations (1) ^^ Tout est clair, juste révise de nouveau :d @ trés bientot ^^ | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 13 Sep 2010, 17:26 Lun 13 Sep 2010, 17:26 | |
| Je vous propose cet exercice:
ABC est un triangle et [AD) la bissectrice intérieure de l'angle A.
M et N sont deux points des deux demi-droites [AB) et [AC) successivement, et qui réalisent: MDA=B et NDA=C(angles)
Les deux droites (AD) et (MN) se coupent en P.
Démontrez que AD^3=AB.AC.AP.
Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 14 Sep 2010, 16:01 Mar 14 Sep 2010, 16:01 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- @nmo: Oui, c'est vrai, la derniére phase est erroné. Mais il y avait une error dans l'énoncé, (x,y,z) sont supposé strictement positives.. Contre exemple: prendre x=y=0 et z=3. Ce qui est n'est pas définie. Ou bien, il faut dire qu'au plus l'un des variables est nulle ^^
Je reprend:
Je voullais juste utiliser des theorémes connus pour s'habituer, et pour leur utilités de ce sujet.. Sinon je peux procéder comme suit:
Solution:
* x+y+z=3 => 2(xy+yz+xz)=9-(x²+y²+z²) , on sait par IAG que: x²+y²+z² >= xy+yz+xz d'ou 2(xy+yz+xz)+xy+yz+xz =< 9 Alors on a: xy+yz+xz =< 3.
* Maintenant j'ai remarqué qu'il suffit de démontrer que: 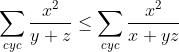 (1) (1)
* On a: 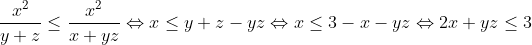
* Alors en emplyant le sigma cyclic, on aura: +xy+yz+xz\leq 9) Ce qui est vrai car Ce qui est vrai car 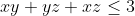
* Par l'AM-HM (Qui est un cas particulier de C.S et prouvable par AM-GM) et en posant:
 et et  et et  et et  et et  et et 
On aura cette inégalité qui est connu: ( \:2(x+y+z)\: ) \:\geq \: (x+y+z)^2)
Donc: 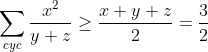
(1) Permet de dire que =\frac{3}{2}) Atteint pour Atteint pour 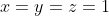
CQFD.. Tu n'a pas bien démontré la relation (1).
Je vais présenter une autre methode maintenant. A ton avis pourquoi je n'ai pas démontrer bien la relation (1) ?
Pour que tu me comprends bien, nmo: Sigma = la somme des nombres. Alors que j'ai fais la somme de chaque deux nombres, l'un appratient au premier Sigma, et le deuxiéme apartient au deuxiéme, alors la somme de ces trois inégalités qu'on aura aprés simplification représente la relations (1) ^^ Tout est clair, juste révise de nouveau :d
@ trés bientot ^^ Tu dis que 2x+yz=<3. Prends ce contre exemple: x=2, y=1/2, et z=1/2. Laisse tomber. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 17 Sep 2010, 18:14 Ven 17 Sep 2010, 18:14 | |
| Je propose un nouvel exercice: x, y, z, et t sont des réels vérifiant  . Déterminez la valeur maximale de l'expression  sachant que  . Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 20 Oct 2010, 23:36 Mer 20 Oct 2010, 23:36 | |
| J'essayerai peut-être de proposer ma solution au dernier exercice de géométrie demain.  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 27 Oct 2010, 16:21 Mer 27 Oct 2010, 16:21 | |
| Avec un peu de retard, mais elle est là quand même : Solution au problème : ADN et ADC sont semblables, et ADM et ABD sont de même semblables. Donc : 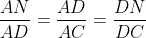 et 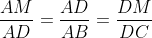 (1) On en déduit en particulier que AD²=AN.AC et AD²=AM.AB. Donc : AD^4 = AB.AC.AN.AM Il reste donc à montrer que AN.AM = AD.AP. ABC étant un triangle, on a A+B+C=180 en tant qu'angles. De fait, MDN+A=180, et par suite, le quadrilatère ANDM est inscriptible. D'après le théorème de Ptolémée appliqué sur ce quadrilatère, on a AD.MN=AN.MD+AM.ND Mais d'après (1), on a : 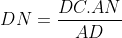 et 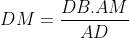 Donc, en continuant sur Ptolémée, on a : }{AD}(DB+DC)%20=%20\frac{AM.AN.BC}{AD}) 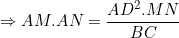 . Il reste donc à montrer que 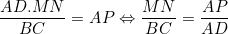 . Maintenant, ANM et ABC sont semblables. Par suite, 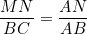 . Et APN et ABD sont semblables. Par suite, 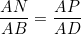 . Par conséquent, 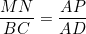 . CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 28 Oct 2010, 17:50 Jeu 28 Oct 2010, 17:50 | |
| - Dijkschneier a écrit:
- Avec un peu de retard, mais elle est là quand même :
Solution au problème :
ADN et ADC sont semblables, et ADM et ABD sont de même semblables.
Donc : 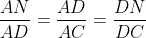 et et 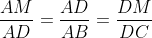 (1) (1)
On en déduit en particulier que AD²=AN.AC et AD²=AM.AB.
Donc : AD^4 = AB.AC.AN.AM
Il reste donc à montrer que AN.AM = AD.AP.
ABC étant un triangle, on a A+B+C=180 en tant qu'angles.
De fait, MDN+A=180, et par suite, le quadrilatère ANDM est inscriptible.
D'après le théorème de Ptolémée appliqué sur ce quadrilatère, on a AD.MN=AN.MD+AM.ND
Mais d'après (1), on a : 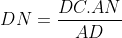 et et 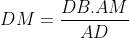
Donc, en continuant sur Ptolémée, on a : }{AD}(DB+DC)%20=%20\frac{AM.AN.BC}{AD})
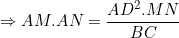 . .
Il reste donc à montrer que 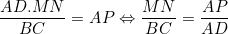 . .
Maintenant, ANM et ABC sont semblables. Par suite, 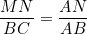 . .
Et APN et ABD sont semblables. Par suite, 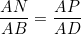 . .
Par conséquent, 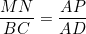 . CQFD. . CQFD. Très bien, une solution exellente, voire élégante. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 28 Oct 2010, 18:55 Jeu 28 Oct 2010, 18:55 | |
| Excusez - moi svp J'ai Une question :
Aux olympiades dans les exercices de géométrie peut-on dire que des triangles sont semblables sans à le prouver juste à partir du dessin puisque c'est clair où faut-il le démontrer avec les angles et les côtés ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 28 Oct 2010, 19:27 Jeu 28 Oct 2010, 19:27 | |
| - Mehdi.O a écrit:
- Excusez - moi svp J'ai Une question :
Aux olympiades dans les exercices de géométrie peut-on dire que des triangles sont semblables sans à le prouver juste à partir du dessin puisque c'est clair où faut-il le démontrer avec les angles et les côtés ? Au Maroc, non, il faut toujours expliquer ce genre de choses. A un niveau plus élevé (j'entends par là le niveau des olympiades internationales), ces considérations, lorsqu'elles ne sont pas fondamentales, peuvent éventuellement être éludées. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Nov 2010, 18:24 Jeu 11 Nov 2010, 18:24 | |
| Inutile d'enterrer ce sujet, voici un exercice, amusez vous à le faire: Résolvez aussi en IN² ce système: \begin{cases}x^2-y^2=7344\\PGCD(x,y)=12\end{cases}) . Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 28 Jan 2011, 15:50 Ven 28 Jan 2011, 15:50 | |
| Même si cela vient trop tard, je dois dire:
Grosso modo, on s'est régalé: plus de 60 exercices délicieux à faire.
Je tiens à remercier et féliciter tous les participants.
C'est la fin de ce jeu, et la naissance d'un autre dans le forum de première.
Ce qui manquait le plus dans ce jeu est la numérotation des problèmes, l'absence de gestion surtout lors du commencement...
La porte n'est pas encore fermée, si quelqu'un a quelque chose à dire ou une solution à proposer, je lui dit bienvenu.
Une discussion des exercices non résolu sera créé dans le forum divers.
Au plaisir! | |
|
  | |
hind nassri
Maître

 Nombre de messages : 143 Nombre de messages : 143
Age : 29
Date d'inscription : 25/01/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 01 Fév 2011, 01:09 Mar 01 Fév 2011, 01:09 | |
| slt svp est ce que vous pouvez me donner la réponse de l'exercice qui est posté sur la page
3 j'ai besoin de lui et j'ai pas trouvé la réponse merci d'avance
IL COMMENCE PAR:
Soit a,b et c des nombres strictement positif
démontrez que
c'est un exercice de nmo
| |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Fév 2011, 21:05 Jeu 03 Fév 2011, 21:05 | |
| svp pouvez vous montrer que pour tout a et b et c appartenant a IR*+:
b/a+c/b+a/c<=81/4 si cela est vrai d'abord et merci d'avance! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Fév 2011, 21:11 Jeu 03 Fév 2011, 21:11 | |
| Cela n'est clairement pas vrai.
Prend a=1 et b tendant vers l'infiini. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Fév 2011, 22:06 Jeu 03 Fév 2011, 22:06 | |
| Ah oui vous avez raison.C'est ma faute dsl.C'est juste une suite de calcul dan un qui m'a tendu a prouver cette inegalite qui est bien clairement fausse . dsl. | |
|
  | |
yasmine
Maître

 Nombre de messages : 71 Nombre de messages : 71
Age : 29
Localisation : terrrrrrrre
Date d'inscription : 09/04/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 11 Avr 2011, 22:44 Lun 11 Avr 2011, 22:44 | |
| oui.la demo de majdouline est juste | |
|
  | |
yasmine
Maître

 Nombre de messages : 71 Nombre de messages : 71
Age : 29
Localisation : terrrrrrrre
Date d'inscription : 09/04/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 11 Avr 2011, 22:44 Lun 11 Avr 2011, 22:44 | |
| oui.la demo de majdouline est juste | |
|
  | |
yasmine
Maître

 Nombre de messages : 71 Nombre de messages : 71
Age : 29
Localisation : terrrrrrrre
Date d'inscription : 09/04/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 11 Avr 2011, 23:21 Lun 11 Avr 2011, 23:21 | |
| [quote="majdouline"][quote="darkpseudo"][quote="majdouline"]y a la solution avec les fonctions(belle et courte)
tu considère la fonction 1/(x+1) qui est croissante sur l'intervalle [0,+00[
on a a<b+c <=>a+1<b+c+1
alors en appliquant 1/(x+1)
on aura:a/(1+a)<(b+c)/(1+b+c)=b/(1+b+c)+c/(1+b+c)<b/(1+b)+c/(1+c)
-------------------------------------------------------------------------
et puis la solution du calcul:(moche et ennuyeuse)
on sait que a<b+c<=>a+ac+ab<b+c+ac+ab<=>a+ac+ab+abc<b+c+ac+ab+2abc+2bc
<=>a(1+c+b+bc)<(b+c+2bc)(1+a)
<=>a(1+c)(1+b)<(b(c+1)(1+a)+c(b+1))(1+a)
<=>a/(1+a)<b/(1+b)+c/(1+c)
| |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 12 Avr 2011, 15:48 Mar 12 Avr 2011, 15:48 | |
| J'ai un exercice pour vs
1) démontrez que a/b + c/d >= 4(ad+bc)/ (b+d)^2
2) conclure que a/(b+2c+d) + b/(c+2d+a) + c/(d+2a+b) + d/ (a+2b+c)
Bonne chance c po tro dur !! | |
|
  | |
Loliiiita
Habitué
 Nombre de messages : 18 Nombre de messages : 18
Age : 28
Date d'inscription : 23/04/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 27 Avr 2011, 20:28 Mer 27 Avr 2011, 20:28 | |
| Amigo-6 , Pour la 2 eme question , je vois vraiment pas ou est la question xD !! Bref J'aii Fait la kestion 1 voila la solution :
On a :
a/b + c/d = (ad + bc)/bd = 4(ad+bc) / 4bd
On compare (b+d)² avec 4bd :
(b+d)²-4bd=b²+d²+2bd-4bd = (b-d)²>0
sa ve dire (b+d)² >= 4bd
donc 1/(b+d)² =< 1/4bd
ce qui ve dire 4(ad+bc)/(b+d)² =< 4(ad+bc)/4bd
C ki ve dire 4(ad+bc)/(b+d)² =< (ad +bc)/4bd
Donc 4(ad+bc)/(b+d)² =< a/b + c/d
Donc a/b + c/d >= 4(ad+bc)/(b+d)² ^^
Ps : Je repete pour la kestion 2 ta pa donné la kestion | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 01 Mai 2011, 18:00 Dim 01 Mai 2011, 18:00 | |
| ex x)
x et y de IR +*
on a f(x).f(y) - f(xy)= y/x+y/x
calcule f(2) | |
|
  | |
manwella
Débutant
 Nombre de messages : 1 Nombre de messages : 1
Age : 28
Date d'inscription : 01/05/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 01 Mai 2011, 18:59 Dim 01 Mai 2011, 18:59 | |
| y a il des règle a savoir avant de passer les olympiades?? | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 01 Mai 2011, 18:59 Dim 01 Mai 2011, 18:59 | |
| | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 01 Mai 2011, 19:43 Dim 01 Mai 2011, 19:43 | |
| Mehdi passe la démonstration pliz
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 01 Mai 2011, 20:06 Dim 01 Mai 2011, 20:06 | |
| En fait, on peut même définir cette fonction:
f(x).f(y)-f(xy)=x/y+y/x.
P(1;1): f(1)=2 ou f(1)=-1
P(x;1): 2f(x)-f(x)=x+1/x ou -f(x)-f(x)=x+1/x
Donc f(x)=x+1/x ou f(x)=-1/2(x+1/x). Inversement on trouve que seule x:-> x+1/x est une solution.
Donc je peux omettre f(2)=-5/4 ... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
