| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 14:06 Lun 30 Aoû 2010, 14:06 | |
| - Dijkschneier a écrit:
- nmo a écrit:
Belle tentative, mais A est naturel.
En effet.
Mauvais calcul.
Je reprends donc : A^3 = 27 [4/3 + 3*(A/3)*7/27 ] = 36 + 7A.
Cela vient de l'identité : (a+b)^3 = a^3 + b^3 + 3(a+b)ab.
Cette équation a une seule racine réelle qui est 4.
Donc A=4, c'est un entier. Bien, je vais le faire avec une autre methode tout de suite. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 14:30 Lun 30 Aoû 2010, 14:30 | |
| - nmo a écrit:
- Bon, je vous propose cet exercice:
Est-ce-que le nombre suivant est un entier?
^{\frac{1}{3}}+\big(\frac{2}{3}-\frac{41}{81}.\sqrt{\frac{5}{3}}\big)^{\frac{1}{3}}\bigg)) . .
Bonne chance. Posons tout d'abord ^{\frac{1}{3}}) , et simplifions-le. On a ^{\frac{1}{3}}) . Donc ^{\frac{1}{3}}) . Donc ^{\frac{1}{3}}) . Donc ^{\frac{1}{3}}) . Donc ^{\frac{1}{3}}) . Donc }{3*3^5}\big)^{\frac{1}{3}}) . Donc ^{\frac{1}{3}}) . Donc ^{\frac{1}{3}}) . Donc ^2+(\sqrt{15})^3+3*6^2*\sqrt{15}}{3^6}\big)^{\frac{1}{3}}) . Donc ^3}{3^6}\big)^{\frac{1}{3}}) . Donc ^{3*\frac{1}{3}}}{3^{6*\frac{1}{3}}}) . Donc ^1}{3^2}) . Donc 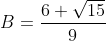 . De même ^{\frac{1}{3}}=\frac{6-\sqrt{15}}{9}) . Du fait, ) . Donc ) . Donc ) . Donc 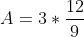 . Donc 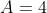 . Ce qui confirme la solution de Dijkschneier. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 15:02 Lun 30 Aoû 2010, 15:02 | |
| - nmo a écrit:
- Je n'ai pas bien lu ce que tu écris, je te dis la même chose que Dijkschneier: Essaie de nouveau car A est naturel.
J'ai passé vitement, mais bon je n'ai pas croyé çelà ! voilà:  De méme:  D'ou: 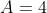 De méme: De méme: http://latex.codecogs.com Décone.
Dernière édition par M.Marjani le Lun 30 Aoû 2010, 15:11, édité 2 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 15:07 Lun 30 Aoû 2010, 15:07 | |
| - M.Marjani a écrit:
- Je n'ai pas croyé à ça avant, nmo ! Bon voilà:
[img]http://latex.codecogs.com/gif.latex?(\frac{2}{3}-\frac{41}{81}*\sqrt{\frac{5}{3}})^{\frac{1}{3}}=\frac{\sqrt[3]{162-41\sqrt{15}}}{3*3^{\frac{2}{3}}}=\frac{1}{9}(6-\sqrt{15})[/img]
De méme: [img]http://latex.codecogs.com/gif.latex?(\frac{2}{3}+\frac{41}{81}*\sqrt{\frac{5}{3}})^{\frac{1}{3}}=\frac{\sqrt[3]{162+41\sqrt{15}}}{3*3^{\frac{2}{3}}}=\frac{1}{9}(6+\sqrt{15})[/img]
D'ou: 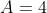 Laisse tomber, c'est mon travail. En plus, Ton latex est illisible. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 15:16 Lun 30 Aoû 2010, 15:16 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Je n'ai pas croyé à ça avant, nmo ! Bon voilà:
[img]http://latex.codecogs.com/gif.latex?(\frac{2}{3}-\frac{41}{81}*\sqrt{\frac{5}{3}})^{\frac{1}{3}}=\frac{\sqrt[3]{162-41\sqrt{15}}}{3*3^{\frac{2}{3}}}=\frac{1}{9}(6-\sqrt{15})[/img]
De méme: [img]http://latex.codecogs.com/gif.latex?(\frac{2}{3}+\frac{41}{81}*\sqrt{\frac{5}{3}})^{\frac{1}{3}}=\frac{\sqrt[3]{162+41\sqrt{15}}}{3*3^{\frac{2}{3}}}=\frac{1}{9}(6+\sqrt{15})[/img]
D'ou: 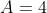 Ton latex est illisible. Codecogs déconne ... - nmo a écrit:
- On demande la réciproque, ce que tu as fait est le contraire.
On peut faire les deux. Ce qui est important qu'elle est démontrer. Si j'avais du temps je vais essayer avec la réciproque. (Je te rappelle que ce n'est pas du façile dans les deux sens  ). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 15:54 Lun 30 Aoû 2010, 15:54 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- Je n'ai pas croyé à ça avant, nmo ! Bon voilà:
[img]http://latex.codecogs.com/gif.latex?(\frac{2}{3}-\frac{41}{81}*\sqrt{\frac{5}{3}})^{\frac{1}{3}}=\frac{\sqrt[3]{162-41\sqrt{15}}}{3*3^{\frac{2}{3}}}=\frac{1}{9}(6-\sqrt{15})[/img]
De méme: [img]http://latex.codecogs.com/gif.latex?(\frac{2}{3}+\frac{41}{81}*\sqrt{\frac{5}{3}})^{\frac{1}{3}}=\frac{\sqrt[3]{162+41\sqrt{15}}}{3*3^{\frac{2}{3}}}=\frac{1}{9}(6+\sqrt{15})[/img]
D'ou: 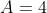 Ton latex est illisible. Codecogs déconne ...
- nmo a écrit:
- On demande la réciproque, ce que tu as fait est le contraire.
On peut faire les deux. Ce qui est important qu'elle est démontrer. Si j'avais du temps je vais essayer avec la réciproque.
(Je te rappelle que ce n'est pas du façile dans les deux sens  ). ). La voie que tu as pris pour l'exercice proposé par Dijkschneier est facile. La réciproque est rude. Codegods ne déconne pas, mais les acollades n'apparaissent pas même avant. Maintenant, je vais réflichir pour les deux exercices sans solution. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 16:23 Lun 30 Aoû 2010, 16:23 | |
| - nmo a écrit:
On peut faire les deux. Ce qui est important qu'elle est démontrer. Si j'avais du temps je vais essayer avec la réciproque.
(Je te rappelle que ce n'est pas du façile dans les deux sens  ). ).
La voie que tu as pris pour l'exercice proposé par Dijkschneier est facile.
La réciproque est rude.Codegods ne déconne pas, mais les acollades n'apparaissent pas même avant.
Maintenant, je vais réflichir pour les deux exercices sans solution. La démonstration qui est façile. Mais pouvoir crée l'idée est difficile cher nmo. Peut-étre que çelà changera ton idée sur la réciproque: La réciproque:L'idée: Il suffit de démontrer que ABCD est un trapéze. Avec: 2MN = AB+CD ; AM=MD ; BN=CN Démo: A toi de jouer ^^ J'essaye plus tard. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 17:08 Lun 30 Aoû 2010, 17:08 | |
| - nmo a écrit:
La réciproque est rude.
Pas tellement. - nmo a écrit:
- Maintenant, je vais réflichir pour les deux exercices sans solution.
Lesquels ? Je n'en vois qu'un. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 30 Aoû 2010, 17:16 Lun 30 Aoû 2010, 17:16 | |
| - Dijkschneier a écrit:
- nmo a écrit:
La réciproque est rude.
Pas tellement.
- nmo a écrit:
- Maintenant, je vais réflichir pour les deux exercices sans solution.
Lesquels ? Je n'en vois qu'un. En plus du tien, il reste celui-là: - M.Marjani a écrit:
- Probléme:
Déterminer tous les couples (x,y) d'entiers relatifs tels que:
 | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 03 Sep 2010, 12:57 Ven 03 Sep 2010, 12:57 | |
| - Dijkschneier a écrit:
- Problème :
Soient M et N les milieux respectifs des segments [AD] et [BC] d'un quadrilatère ABCD. Si 2MN = AB+CD, montrer que (AB) // (CD). Reportons le plan au repère ) . On a d'emblée ) , ) , et ) . Posons ) . On a M le milieu de [AD]. Donc ) . Donc ) . Donc ) . Donc ) . De même, on trouve que ) . Et on a ) . Donc ) . Donc ) . Donc ) .==>(1) D'autre part, on a ) . Et ) . Donc ) . Donc ) . Et par suite, ) . Donc ) .==>(2) De 1 et 2, on trouve que 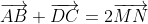 . On a maintenant 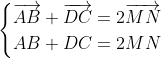 . Donc ^2=(2\overrightarrow{MN})^2\\(AB+DC)^2=(2MN)^2\end{cases}) . Donc 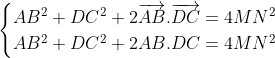 . Donc 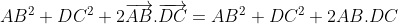 . Donc 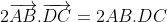 . Donc 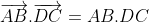 . Donc }=AB.DC) . Et puisque AB.DC se diffère de 0, alors }=1) . Et on sait que 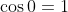 . Donc }=\cos{0}) . Donc 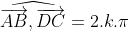 tel que k est un entier. Donc, les deux vecteurs 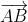 et 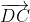 sont colinéaires. Donc les droites (AB) et (DC) sont parallèles. CQFD. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 03 Sep 2010, 14:29 Ven 03 Sep 2010, 14:29 | |
| Oui nmo, mais c'était pas nécessaire de passer par le calcul analytique. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 05 Sep 2010, 17:22 Dim 05 Sep 2010, 17:22 | |
| - Dijkschneier a écrit:
- Problème :
Soient M et N les milieux respectifs des segments [AD] et [BC] d'un quadrilatère ABCD. Si 2MN = AB+CD, montrer que (AB) // (CD). Solution alternative :Soit O le milieu de [AC]. Dans le triangle ADC, M et O sont respectivement les milieux de [AD] et de [AC]. Selon le théorème de Thalès, 2OM = DC. Dans le triangle ABC, O et N sont respectivement les milieux de [AC] et de [BC]. Selon le théorème de Thalès, 2ON = AB. Par somme : 2(OM+ON)=DC+AB. Mais puisque DC+AB=2MN, alors par transitivité de la relation d'égalité, on a OM+ON=MN. Cela veut dire que O appartient à [MN]. Maintenant, dans le triangle ADC, M et O sont respectivement les milieux de [AD] et [AC]. Selon le théorème de Thalès, (OM)//(DC)). Or (OM)=(MN), donc (MN)//(DC). Et de même en considérant le triangle ABC : (MN)//(AB) Par transitivité de la relation de parallélisme, il vient que (AB)//(DC). | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 07 Sep 2010, 13:09 Mar 07 Sep 2010, 13:09 | |
| - M.Marjani a écrit:
- Probléme:
Déterminer tous les couples (x,y) d'entiers relatifs tels que:
 Posons a=x+4. On a (x+7)(x+8 )=y^2) . Donc (x+4-3)(x+4+3)(x+4+4)=y^2) . Donc (a-3)(a+3)(a+4)=y^2) . Donc (a^2-9)=y^2) . Donc 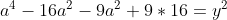 . Donc 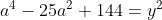 . Donc 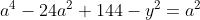 . Donc ^2-y^2=a^2) . Donc (a^2-12+y)=a^2) . Le premier cas: 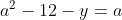 et 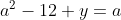 . On a 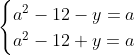 . Donc 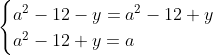 . Donc 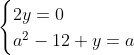 . Donc 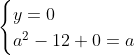 . Donc 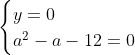 . Donc 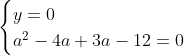 . Donc -4(a+3)=0\end{cases}) . Donc (a+3)=0\end{cases}) . Donc 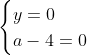 ou 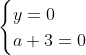 . Donc 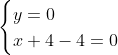 ou 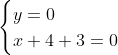 . Donc 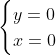 ou 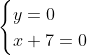 . Donc 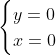 ou 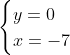 . Ainsi les deux couples ) et ) sont solutions au problème. Le second cas: 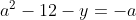 et 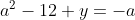 . On a 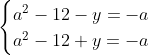 . Donc 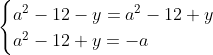 . Donc 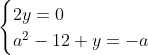 . Donc 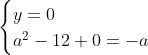 . Donc 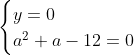 . Donc 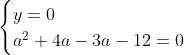 . Donc +4(a-3)=0\end{cases}) . Donc (a-3)=0\end{cases}) . Donc 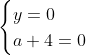 ou 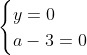 . Donc 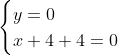 ou 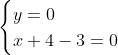 . Donc 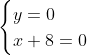 ou 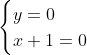 . Donc 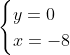 ou 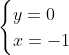 . Ainsi les deux couples ) et ) sont solutions au problème. Le troisième cas: 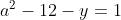 et 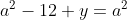 . On a 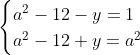 . Donc 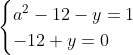 . Donc 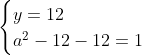 . Donc 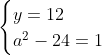 . Donc 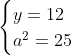 . Donc 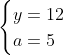 ou 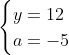 . Donc 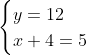 ou 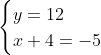 . Donc 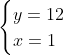 ou 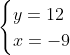 . Ainsi les deux couples ) et ) sont solutions au problème. Le quatrième cas: 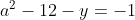 et 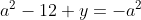 . On a 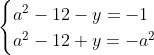 . Donc 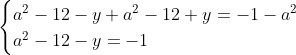 . Donc 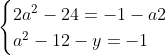 . Donc 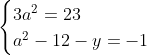 . Donc 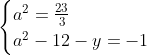 . Ce qui contredit le fait que a est entier. Le cinquième cas: 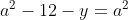 et 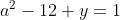 . On a 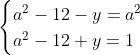 . Donc 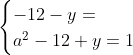 . Donc 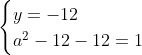 . Donc 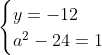 . Donc 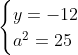 . Donc 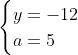 ou 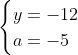 . Donc 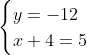 ou 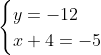 . Donc 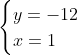 ou 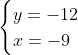 . Ainsi les deux couples ) et ) sont solutions au problème. Le dernier cas: 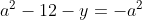 et 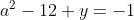 . On a 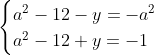 . Donc 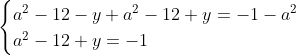 . Donc 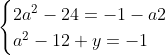 . Donc 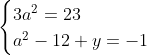 . Donc 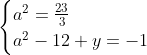 . Ce qui contredit le fait que a est entier. Synthèse: Soit S l'ensemble des solutions du problème: ;(-1,0);(-7,0);(-8,0);(1,12);(-9,12);(1,-12);(-9,-12)\}) . Et c'est fini, sauf erreur.
Dernière édition par nmo le Mer 08 Sep 2010, 15:00, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 07 Sep 2010, 13:12 Mar 07 Sep 2010, 13:12 | |
| - Dijkschneier a écrit:
- Dijkschneier a écrit:
- Problème :
Soient M et N les milieux respectifs des segments [AD] et [BC] d'un quadrilatère ABCD. Si 2MN = AB+CD, montrer que (AB) // (CD). Solution alternative :
Soit O le milieu de [AC].
Dans le triangle ADC, M et O sont respectivement les milieux de [AD] et de [AC]. Selon le théorème de Thalès, 2OM = DC.
Dans le triangle ABC, O et N sont respectivement les milieux de [AC] et de [BC]. Selon le théorème de Thalès, 2ON = AB.
Par somme : 2(OM+ON)=DC+AB. Mais puisque DC+AB=2MN, alors par transitivité de la relation d'égalité, on a OM+ON=MN. Cela veut dire que O appartient à [MN].
Maintenant, dans le triangle ADC, M et O sont respectivement les milieux de [AD] et [AC]. Selon le théorème de Thalès, (OM)//(DC)). Or (OM)=(MN), donc (MN)//(DC).
Et de même en considérant le triangle ABC : (MN)//(AB)
Par transitivité de la relation de parallélisme, il vient que (AB)//(DC).
Vraiment, c'est du bon travail. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 07 Sep 2010, 13:16 Mar 07 Sep 2010, 13:16 | |
| Je vous propose cet exercice: x, y, et z sont des réels positifs, tel que x+y+z=3. Déterminer la valeur minimale que peut atteindre l'expression A: 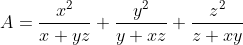 . Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 07 Sep 2010, 15:09 Mar 07 Sep 2010, 15:09 | |
| Un exercice de plus: Determinez les deux solutions de l'équation 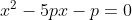 pour que A atteint sa valeur minimale: 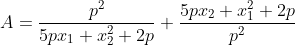 . Bonne chance. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 08 Sep 2010, 14:43 Mer 08 Sep 2010, 14:43 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Probléme:
Déterminer tous les couples (x,y) d'entiers relatifs tels que:
 Posons a=x+4.
On a (x+7)(x+8 )=y^2) . .
Donc (x+4-3)(x+4+3)(x+4+4)=y^2) . .
Donc (a-3)(a+3)(a+4)=y^2) . .
Donc (a^2-9)=y^2) . .
Donc 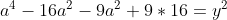 . .
Donc 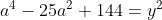 . .
Donc 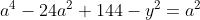 . .
Donc ^2-y^2=a^2) . .
Donc (a^2-12+y)=a^2) . .
Le premier cas: 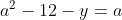 et et 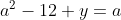 . .
On a 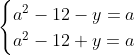 . .
Donc 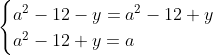 . .
Donc 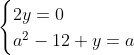 . .
Donc 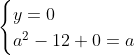 . .
Donc 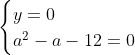 . .
Donc 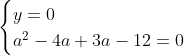 . .
Donc -4(a+3)=0\end{cases}) . .
Donc (a+3)=0\end{cases}) . .
Donc 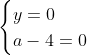 ou ou 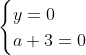 . .
Donc 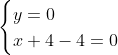 ou ou 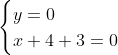 . .
Donc 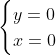 ou ou 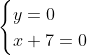 . .
Donc 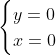 ou ou 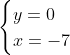 . .
Ainsi les deux couples ) et et ) sont solutions au problème. sont solutions au problème.
Le second cas: 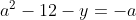 et et 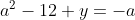 . .
On a 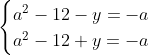 . .
Donc 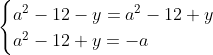 . .
Donc 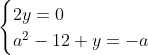 . .
Donc 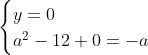 . .
Donc 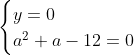 . .
Donc 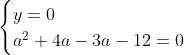 . .
Donc +4(a-3)=0\end{cases}) . .
Donc (a-3)=0\end{cases}) . .
Donc 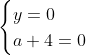 ou ou 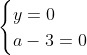 . .
Donc 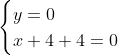 ou ou 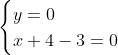 . .
Donc 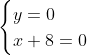 ou ou 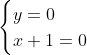 . .
Donc 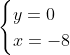 ou ou 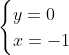 . .
Ainsi les deux couples ) et et ) sont solutions au problème. sont solutions au problème.
Le troisième cas: 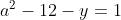 et et 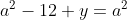 . .
On a 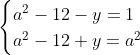 . .
Donc 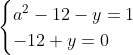 . .
Donc 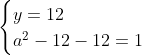 . .
Donc 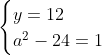 . .
Donc 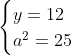 . .
Donc 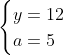 ou ou 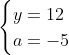 . .
Donc 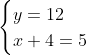 ou ou 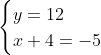 . .
Donc 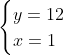 ou ou 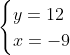 . .
Ainsi les deux couples ) et et ) sont solutions au problème. sont solutions au problème.
Le quatrième cas: 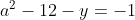 et et 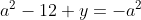 . .
On a 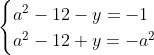 . .
Donc 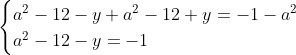 . .
Donc 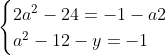 . .
Donc 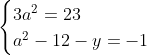 . .
Donc 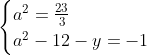 . .
Ce qui contredit le fait que a est entier.
Le cinquième cas: 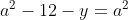 et et 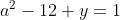 . .
On a 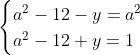 . .
Donc 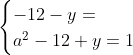 . .
Donc 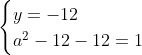 . .
Donc 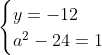 . .
Donc 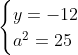 . .
Donc 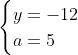 ou ou 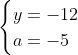 . .
Donc 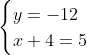 ou ou 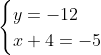 . .
Donc 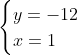 ou ou 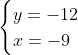 . .
Ainsi les deux couples ) et et ) sont solutions au problème. sont solutions au problème.
Le dernier cas: 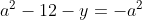 et et 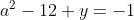 . .
On a 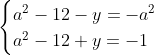 . .
Donc 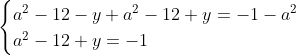 . .
Donc 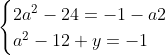 . .
Donc 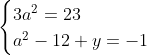 . .
Donc 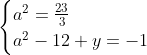 . .
Ce qui contredit le fait que a est entier.
Synthèse:
Soit S l'ensemble des solutions du problème:
;(-1,0);(-7,0);(-8,0);(1,12);(-9,12);(-1,12);(-9,-12)\}) . .
Et c'est fini, sauf erreur. Un bon travaille. Bravo ! Mais t'as raté quelques couples: {(-4,-12) ; (-4,12)} T'as fais une faute de frappe également: (1, 12) et (1, -12) au lieu de (-1, 12) et (1, 12). Solution proposé: PS: PS: J'avais une autre methode trés façile avec le déscriment (trés arithmétique) belle qui donne (0,0) et les 9 solutions: y²=36a² (Aprés simplification + Discrément +.. on aura: a=0 ou 2x=<a^4) Et: tx=-6(3+a²V(t)) Ou tx=-6(3-a²V(t)) Avec t=(x+8 )²+23 , et happe.. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 08 Sep 2010, 16:57 Mer 08 Sep 2010, 16:57 | |
| - nmo a écrit:
- Je vous propose cet exercice:
x, y, et z sont des réels positifs, tel que x+y+z=3.
Déterminer la valeur minimale que peut atteindre l'expression A:
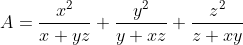 . .
Bonne chance. Ma Solution:Par IAG:  Une autre IAG sur (x+yz) , (y+xz) et (z+xy) donne: (y+xz)(z+xy)\leq (\frac{1}{3}(x+yz+y+xz+z+xy))^3) )^3) (1) (1)Par la symétrie des roles, on suppose x>=y>=z et appliquant Chebyshev: .(\sum_{i=1}^{n}b_i)) (y+z+x)=3) Alors (1) devient inférieur ou égale à  Donc:  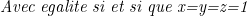 Le résultat est clair: Min(A)=3/2. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 10 Sep 2010, 11:22 Ven 10 Sep 2010, 11:22 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 10 Sep 2010, 18:09 Ven 10 Sep 2010, 18:09 | |
| | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 11 Sep 2010, 12:49 Sam 11 Sep 2010, 12:49 | |
| | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 11 Sep 2010, 14:33 Sam 11 Sep 2010, 14:33 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 13 Sep 2010, 15:38 Lun 13 Sep 2010, 15:38 | |
| - tarask a écrit:
- nmo a écrit:
- Un exercice de plus:
Determinez les deux solutions de l'équation 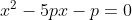 pour que A atteint sa valeur minimale: pour que A atteint sa valeur minimale:
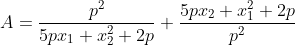 . .
Bonne chance. Voilà ma tentative :

Sauf erreur et bonne chance  Juste une faute de calcul: c'est -1/8 au lieu de 1/8 à la fin. Dans ce cas, l'équation n'admet pas de solution. Et on met fin à l'exercice. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 13 Sep 2010, 15:47 Lun 13 Sep 2010, 15:47 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 13 Sep 2010, 16:04 Lun 13 Sep 2010, 16:04 | |
| - nmo a écrit:
- Je vous propose cet exercice:
x, y, et z sont des réels positifs, tel que x+y+z=3.
Déterminer la valeur minimale que peut atteindre l'expression A:
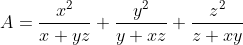 . .
Bonne chance. On a 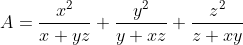 . Donc =\frac{x^2}{x+yz}-x+\frac{y^2}{y+xz}-y+\frac{z^2}{z+xy}-z) . Donc 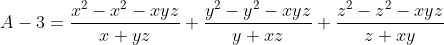 . Donc 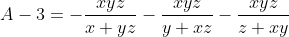 . Donc ) . Donc ) . D'autre part, selon IAG, on a 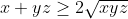 . Donc 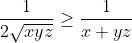 . De même, 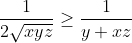 . Et 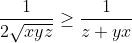 . Soit en sommant, 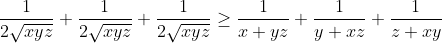 . Donc 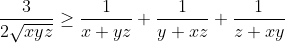 . Donc ) . Donc 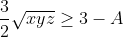 .==>(1) D'autre part, selon IAG, on a ^3\ge27xyz) . Donc ^3\ge27xyz) . Donc 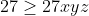 . Donc 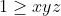 . Donc 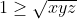 . Donc 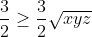 .==>(2) De 1 et 2, on déduit que 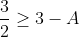 . Donc 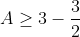 . Donc 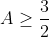 . Ce qui met fin à la démonstration. L'égalité aura lieu si et seulement si x=y=z=1. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
