Préparations aux olympiades de tronc commun (2009-2010)

Vas-y, donne tes solutions, M.Marjani.
Je n'ai pas de réponse à donner.

Bonsoir Dijkschneier;

Pour le probléme 1; Je vous prommis de donner ma réponse prochainement. Faisiez un petit essaie, ce n'est que de petites factorisation qui donnent la solution.

Et pour rendre le probléme 2 plus sympa, j'ajoute quelque chose:

M.Marjani a écrit:

Vous ajoutez aussi:

Probléme 2 :

Ecrire le nombre suivant sous forme de



Bonne chance.

Bla bla bla bla...
Tu as les réponses ou pas ?

Dijkschneier a écrit:

Tu as les réponses ou pas ?

Ouiii !!!!! et avec plusieurs methodes !! Si tu n'as pas pu les résoudre priére de laisser les autres essayer !!!!!!

Solution 1:

Le nombre qu'on veut calculer est equivalent à 10 nomes parmi eux on cite:
(1)

De méme: (2)
.
.

.
(De méme pour les 8 autres nomes ....)

En sommant (1) et (2) et ... et (10):





On déduit qu'on peut appliqué ce petit theoréme sur d'autres nombres.. Qui est le cas géneralisé.

Pour le cas de notre exercise: n=10 avec m=10 ( ''m'' désigne le nombre de nomes (الحدود) dans le nombre de départ que l'on veut calculer )

Comment trouver "m" ?: Du premier coup on peut remarqué que m=(a-b)+1
Avec: "a" le premier nombre (ou chiffre) du dominateur du dérnier nome. "b" le premier nombre (ou chiffre) du dominateur du premier nome. Pour notre EX: m=(19-10)+1=10
CQFD.

_{Crée par moi sauf error.}

Tu te fous de moi ?!
T'arrive-t-il de lire ce que j'écris ?
Pour tes pauvres yeux, je vais quand même citer que j'avais écrit :

Citation :

Ce problème se ramène à calculer la somme des nombres 1/(2i+1).
Il n'y a pas de formule générale simple pour calculer des sommes du genre.
Ainsi, la solution que l'on peut apporter reste numérique, et auquel cas, ton problème n'est pas adapté pour les troncs communs.
La section collège serait plus appropriée.
Par exemple : = 1/2 [ 1/23 + 1/25 + ... + 1/41 ]

Pitoyable...

Dijkschneier a écrit:

Tu te fous de moi ?!
T'arrive-t-il de lire ce que j'écris ?
= 1/2 [ 1/23 + 1/25 + ... + 1/41 ]

Calmes-toi s'il te plaît !

Je t'ai répondu dans un message ... Et puis un mp ...

Si tu as bien lu ce que j'ai demander à prouver, tu vas mieux te calmer un peu... Ta réponse ne répond pas à mon exercise.

Et pour indice j'ai éclairer tant la question, j'ai ajouter de l'écrire de cette forme:

Moi je demande une formule simple pour calculer tous les nombres de cette forme !

Ce n'est pas normale çelà Dijkschneier, il fallait changer de comportement... Bon oublie ...

Je poste la solution du deuxiéme plus tard...

Je laisse la liberté à tous pour poster le prochain EX ...

M.Marjani a écrit:

Dijkschneier a écrit:

Tu te fous de moi ?!
T'arrive-t-il de lire ce que j'écris ?
= 1/2 [ 1/23 + 1/25 + ... + 1/41 ]

Moi je demande une formule simple pour calculer tous les nombres de cette forme !

Je veux bien, mais le calcul d'une série harmonique n'est pas simple. La complexité de la formule que j'ai proposé et que tu as recopié demeure semblable.
Par conséquent, ce problème est du pure n'importe quoi !

De deux, soit :
- Poser de véritables problèmes avec de véritables solutions et de niveau approprié ;
- S'abstenir et passer son chemin.

Dijkschneier a écrit:

Je veux bien, mais le calcul d'une série harmonique n'est pas simple. La complexité de la formule que j'ai proposé et que tu as recopié demeure semblable.

(De 1 ---> m)

Bon, oublie : ) . A toi de proposer le prochain EX pour ne pas perdre du temps donc.

Je n'ai pas de problème à proposer. Que chacun se sente libre d'en proposer un.

M.Marjani a écrit:

Solution 1:

Le nombre qu'on veut calculer est equivalent à 10 nomes parmi eux on cite:
(1)

De méme: (2)
.
.

.
(De méme pour les 8 autres nomes ....)

En sommant (1) et (2) et ... et (10):





On déduit qu'on peut appliqué ce petit theoréme sur d'autres nombres.. Qui est le cas géneralisé.

Pour le cas de notre exercise: n=10 avec m=10 ( ''m'' désigne le nombre de nomes (الحدود) dans le nombre de départ que l'on veut calculer )

Comment trouver "m" ?: Du premier coup on peut remarqué que m=(a-b)+1
Avec: "a" le premier nombre (ou chiffre) du dominateur du dérnier nome. "b" le premier nombre (ou chiffre) du dominateur du premier nome. Pour notre EX: m=(19-10)+1=10
CQFD.

_{Crée par moi sauf error.}

Si c'est un cas général pour calculer cette somme, ce doit être simple, et plus important : donner un résultat. Où est le résultat numérique?

M.Marjani a écrit:

Probléme :
Soit (x,y,z) des réels positive non nulls tel que x > y. Montrez que:

EDIT: (x,y,z) non nulls !
EDIT: (Mathlinks déconne xd)
EDIT: x>y relation évidente.

L'IAG corrobore que .==>(a)
Alors, il suffit de démontrer que .==>(b)
Je procède par équivalence:
On a .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .==>(1)
D'autre part, on sait que pour tout a et b deux réels positifs, avec égalité si et seulement si a=b=0.
Posons a=x+y et b=x-y, il vient que .
Donc .
Donc .
Donc .
Donc .==>(2)
De 1 et 2, il suffi de démontrer que .
Donc .
Donc .
Donc .
Donc .
Donc .
Ce qui est juste, car selon IAG et a fortiori .
De a et b, et de la conclusion de la démonstration par équivalence, on déduit le résultat voulu.
L'égalité aura lieu si x+y=0 et si x-y=0.
Donc x=y=0.
Or, l'inégalité n'est pas définie dans ce cas.
Ce qui assure l'inégalité stricte.
Sauf erreur.

Bon, je vous propose cet exercice:
Est-ce-que le nombre suivant est un entier?
.
Bonne chance.

Démonstration simple et précise. Bravo!

nmo a écrit:

M.Marjani a écrit:

Probléme :
Soit (x,y,z) des réels positive non nulls tel que x > y. Montrez que:

EDIT: (x,y,z) non nulls !
EDIT: (Mathlinks déconne xd)
EDIT: x>y relation évidente.

L'IAG corrobore que .==>(a)
Alors, il suffit de démontrer que .==>(b)
Je procède par équivalence:
On a .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .==>(1)
D'autre part, on sait que pour tout a et b deux réels positifs, avec égalité si et seulement si a=b=0.
Posons a=x+y et b=x-y, il vient que .
Donc .
Donc .
Donc .
Donc .==>(2)
De 1 et 2, il suffi de démontrer que .
Donc .
Donc .
Donc .
Donc .
Donc .
Ce qui est juste, car selon IAG et a fortiori .
De a et b, et de la conclusion de la démonstration par équivalence, on déduit le résultat voulu.
L'égalité aura lieu si x+y=0 et si x-y=0.
Donc x=y=0.
Or, l'inégalité n'est pas définie dans ce cas.
Ce qui assure l'inégalité stricte.
Sauf erreur.

Belle démonstration nmo !!

Je voullais juste dire que cette inégalité est crée par moi. Aprés 3 lemmes crée par M.Marjani l'inégalité serait prouvé :p

Je posterai ma solution plus tard :p

M.Marjani a écrit:

nmo a écrit:

Juste il fallait démontrer pourquoi: De (1) et (2) il suffit démontrer que

Afin de démontrer que a>=c.
On trouve un réel b qui satisfait les deux conditions a>=b et b>=c.
Et le résultat en découle.

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

Juste il fallait démontrer pourquoi: De (1) et (2) il suffit démontrer que

Afin de démontrer que a>=c.
On trouve un réel b qui satisfait les deux conditions a>=b et b>=c.
Et le résultat en découle.

C'est bon.

Ou bien par la division de (1) sur (2)

C'est bien comme démonstration, nmo.

Que direz vous de cette inégalité, elle mérite qu'elle serait posté dans un olymp de premiére nn?

M.Marjani a écrit:

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

Juste il fallait démontrer pourquoi: De (1) et (2) il suffit démontrer que

Afin de démontrer que a>=c.
On trouve un réel b qui satisfait les deux conditions a>=b et b>=c.
Et le résultat en découle.

Ou bien par la division de (1) sur (2)
C'est bien comme démonstration, nmo.
Que direz vous de cette inégalité, elle mérite qu'elle serait posté dans un olymp de premiére nn?

Elle est excellente, j'attends ta démonstration ici https://mathsmaroc.jeun.fr/inegalites-f2/une-inegalite-difficile-a-montrer-mais-joli-t16418.htm.

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

M.Marjani a écrit:

nmo a écrit:

Juste il fallait démontrer pourquoi: De (1) et (2) il suffit démontrer que

Afin de démontrer que a>=c.
On trouve un réel b qui satisfait les deux conditions a>=b et b>=c.
Et le résultat en découle.

Ou bien par la division de (1) sur (2)
C'est bien comme démonstration, nmo.
Que direz vous de cette inégalité, elle mérite qu'elle serait posté dans un olymp de premiére nn?

Elle est excellente, j'attends ta démonstration ici https://mathsmaroc.jeun.fr/inegalites-f2/une-inegalite-difficile-a-montrer-mais-joli-t16418.htm.

La voiçi : https://mathsmaroc.jeun.fr/inegalites-f2/une-inegalite-difficile-a-montrer-mais-joli-t16418.htm#140181

Je vous encourage ! Car de grands membres n'ont pu pas la résoudre :p

nmo a écrit:

Bon, je vous propose cet exercice:
Est-ce-que le nombre suivant est un entier?
.
Bonne chance.

A^3 = 27[4/3 + 3A*7/27] = 36 + 21A, ce qui implique que A^3 = 36 + 21A.
Alternativement, soit on considère que :
- Ceci est une équation du troisième degré, qui a deux solutions non entières et une solution entière mais négative qui est -3, que l'on considère pas car A est strictement positif.
A n'est donc pas un entier.
- A est un entier par l'absurde, et -3 est une solution triviale à l'équation A^3 = 36 + 21A, ce qui par division euclidienne se ramène à l'équation A² = 3A + 12, et par conséquent A est multiple de 3, et par suite A = 3n, et par conséquent, 9n² = 9n + 12, ce qui n'est pas possible car 9 ne divise pas 12. Contradiction. A n'est pas un entier.

Problème :
Soient M et N les milieux respectifs des segments [AD] et [BC] d'un quadrilatère ABCD. Si 2MN = AB+CD, montrer que (AB) // (CD).

Dijkschneier a écrit:

nmo a écrit:

Bon, je vous propose cet exercice:
Est-ce-que le nombre suivant est un entier?
.
Bonne chance.

A^3 = 27[4/3 + 3A*7/27] = 36 + 21A, ce qui implique que A^3 = 36 + 21A.
Alternativement, soit on considère que :
- Ceci est une équation du troisième degré, qui a deux solutions non entières et une solution entière mais négative qui est -3, que l'on considère pas car A est strictement positif.
A n'est donc pas un entier.
- A est un entier par l'absurde, et -3 est une solution triviale à l'équation A^3 = 36 + 21A, ce qui par division euclidienne se ramène à l'équation A² = 3A + 12, et par conséquent A est multiple de 3, et par suite A = 3n, et par conséquent, 9n² = 9n + 12, ce qui n'est pas possible car 9 ne divise pas 12. Contradiction. A n'est pas un entier.

Soit on pose 2/3=a Et: (41/81)*V(5/3)=b . Alors A=3( (a+b)^{1/3} + (a-b)^{1/3} ).
A est un entiére si et si que: a+b=t^3 (t£ IQ+} Et a-b=c^3 (c£IQ+) Car 2/3>(41/81)*V(5/3)>0.

Prenons par exemple a+b qui est égale à (162V(3)+123V(5))÷(243V(3)) = 54V(3)+41V(5) ÷ 81V(3).

54V(3)+41V(5) est différent d'un format x^3 ainsi que 81V(3) qui est d'un format carré. D'aprés ce qui est en haut, çelà est absurde. Donc A n'est pas un entier.

Dijkschneier a écrit:

Problème :
Soient M et N les milieux respectifs des segments [AD] et [BC] d'un quadrilatère ABCD. Si 2MN = AB+CD, montrer que (AB) // (CD).

Ma Solution:

La Figur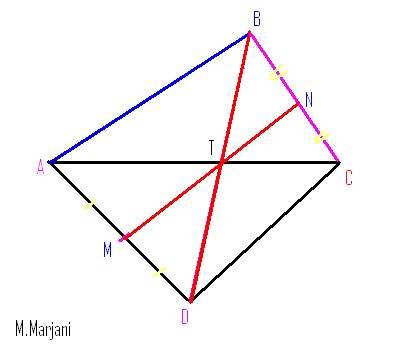e:



La Methode:

L'idée: On suppose que (AB)//(CD) et on démontre que 2MN=AB+CD. Aprés crée Le triangle ACD et M le milieu de [AD], on déssine (MT) paralléle à (CD) tel que T le point d'intersection de (MT) et (AC). Puis on déssine [AB] tel que (AB)//(CD) et B le point d'intersection de (DT) et (AB). N est le milieu de [BC] automatiquement.

Demo: On applique thalés deux fois sur les triangles ABC et ACD:

Sur ABC: Puisque (TN)//(AB) et (C,N,B) ; (A,T,C) allignés (respc.) alors: CN/BC=1/2=TN/AB d'ou (1/2)AB=TN ==> (1)
La méme démarche sur ACD: donc MT=(1/2)CD ==> (2)

(1) + (2) : MN=(1/2)(AB+CD) <=> 2MN=AB+CD


Probléme:

Déterminer tous les couples (x,y) d'entiers relatifs tels que:

Dijkschneier a écrit:

nmo a écrit:

Bon, je vous propose cet exercice:
Est-ce-que le nombre suivant est un entier?
.
Bonne chance.

A^3 = 27[4/3 + 3A*7/27] = 36 + 21A, ce qui implique que A^3 = 36 + 21A.
Alternativement, soit on considère que :
- Ceci est une équation du troisième degré, qui a deux solutions non entières et une solution entière mais négative qui est -3, que l'on considère pas car A est strictement positif.
A n'est donc pas un entier.
- A est un entier par l'absurde, et -3 est une solution triviale à l'équation A^3 = 36 + 21A, ce qui par division euclidienne se ramène à l'équation A² = 3A + 12, et par conséquent A est multiple de 3, et par suite A = 3n, et par conséquent, 9n² = 9n + 12, ce qui n'est pas possible car 9 ne divise pas 12. Contradiction. A n'est pas un entier.

Belle tentative, mais A est naturel.

M.Marjani a écrit:

Soit on pose 2/3=a Et: (41/81)*V(5/3)=b . Alors A=3( (a+b)^{1/3} + (a-b)^{1/3} ).
A est un entiére si et si que: a+b=t^3 (t£ IQ+} Et a-b=c^3 (c£IQ+) Car 2/3>(41/81)*V(5/3)>0.
Prenons par exemple a+b qui est égale à (162V(3)+123V(5))÷(243V(3)) = 54V(3)+41V(5) ÷ 81V(3).
54V(3)+41V(5) est différent d'un format x^3 ainsi que 81V(3) qui est d'un format carré. D'aprés ce qui est en haut, çelà est absurde. Donc A n'est pas un entier.

Je n'ai pas bien lu ce que tu écris, je te dis la même chose que Dijkschneier: Essaie de nouveau car A est naturel.

M.Marjani a écrit:

Dijkschneier a écrit:

Problème :
Soient M et N les milieux respectifs des segments [AD] et [BC] d'un quadrilatère ABCD. Si 2MN = AB+CD, montrer que (AB) // (CD).

Ma Solution:
La Figure:

La Methode:
L'idée: On suppose que (AB)//(CD) et on démontre que 2MN=AB+CD. Aprés crée Le triangle ACD et M le milieu de [AD], on déssine (MT) paralléle à (CD) tel que T le point d'intersection de (MT) et (AC). Puis on déssine [AB] tel que (AB)//(CD) et B le point d'intersection de (DT) et (AB). N est le milieu de [BC] automatiquement.
Demo: On applique thalés deux fois sur les triangles ABC et ACD:
Sur ABC: Puisque (TN)//(AB) et (C,N,B) ; (A,T,C) allignés (respc.) alors: CN/BC=1/2=TN/AB d'ou (1/2)AB=TN ==> (1)
La méme démarche sur ACD: donc MT=(1/2)CD ==> (2)
(1) + (2) : MN=(1/2)(AB+CD) <=> 2MN=AB+CD

On demande la réciproque, ce que tu as fait est le contraire.

nmo a écrit:

Belle tentative, mais A est naturel.

En effet.
Mauvais calcul.
Je reprends donc : A^3 = 27 [4/3 + 3*(A/3)*7/27 ] = 36 + 7A.
Cela vient de l'identité : (a+b)^3 = a^3 + b^3 + 3(a+b)ab.
Cette équation a une seule racine réelle qui est 4.
Donc A=4, c'est un entier.