| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Ven 30 Avr 2010, 20:25 | |
| - M.Marjani a écrit:
- Regarde bien la troisiéme ligne:
kx-ky=k²-2yk <=> -ky+kx=k²-2yk
La premiére cas: k=x=y on a prouver qui est faux.
donc il reste que: -y=k et x=-2y.
Comme si t'as une polynome, si tu veux voir combien vaut a et b et c.. Si j'ai dit a+b=2. Quelle sera la valeur de a^2-b^2? Explique-moi bien. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Ven 30 Avr 2010, 20:48 | |
| lol, ce n'est pas un contre exemple ça, c'est du l'ignorance de répondre à une question comme celle-ci xD Bon, puisque nous avons k qui se répete dans les deux cotés -ky+kx=k²-2ykIl ya deux cas à mon avis  | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Ven 30 Avr 2010, 20:55 | |
| - M.Marjani a écrit:
- lol, ce n'est pas un contre exemple ça, c'est du l'ignorance de répondre à une question comme celle-ci xD
Bon, puisque nous avons k qui se répete dans les deux cotés
-ky+kx=k²-2yk
Il ya deux cas à mon avis La question que j'ai donné ressemble bien au défi que j'ai proposé. Pourquoi tu as répondu là? Et on ne peut pas répondre ici.
Dernière édition par nmo le Ven 30 Avr 2010, 21:48, édité 1 fois | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Ven 30 Avr 2010, 20:56 | |
| -ky+kx=k²-2yk
-5y+5x=25-10y
Combien vaut x et y?
y=2,x=5 => faux, car x+y=5
x=-2y,y=-5 => x=10 et y=-5 => x+y=5, ce qui est juste.
--'
Dernière édition par M.Marjani le Dim 02 Mai 2010, 09:37, édité 1 fois | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Ven 30 Avr 2010, 21:30 | |
| - nmo a écrit:
- M.Marjani a écrit:
- lol, ce n'est pas un contre exemple ça, c'est du l'ignorance de répondre à une question comme celle-ci xD
Bon, puisque nous avons k qui se répete dans les deux cotés
-ky+kx=k²-2yk
Il ya deux cas à mon avis La question que j'ai donné ressemble bien au défi que j'ai proposé.
Pourquoi tu as répondé là?
Et on ne peut pas répondre ici. Car nous avons k qui se répete dans les deux cotés. | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Ven 30 Avr 2010, 21:49 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- lol, ce n'est pas un contre exemple ça, c'est du l'ignorance de répondre à une question comme celle-ci xD
Bon, puisque nous avons k qui se répete dans les deux cotés
-ky+kx=k²-2yk
Il ya deux cas à mon avis La question que j'ai donné ressemble bien au défi que j'ai proposé.
Pourquoi tu as répondé là?
Et on ne peut pas répondre ici. Car nous avons k qui se répete dans les deux cotés. Laisse tomber, ta solution est fausse. Essaie de changer d'optique. | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sam 01 Mai 2010, 13:02 | |
| - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- lol, ce n'est pas un contre exemple ça, c'est du l'ignorance de répondre à une question comme celle-ci xD
Bon, puisque nous avons k qui se répete dans les deux cotés
-ky+kx=k²-2yk
Il ya deux cas à mon avis La question que j'ai donné ressemble bien au défi que j'ai proposé.
Pourquoi tu as répondé là?
Et on ne peut pas répondre ici. Car nous avons k qui se répete dans les deux cotés. Laisse tomber, ta solution est fausse.
Essaie de changer d'optique. L'exercice est de remarquer une certaine chose. La résolutio directe ne donne rien. La solution complète dans mon prochain message. | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sam 01 Mai 2010, 13:21 | |
| - nmo a écrit:
- Voic un exercice de défi de l'année passée:
a et b sont deux réels vérifiant ^{2006}) .
Calculez  .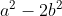
Bonne chance. D'une part: On a ^{2}=1+2\sqrt{2}+(\sqrt{2})^2) . Donc ^{2}=1+2\sqrt{2}+2) . Donc ^{2}=3+2\sqrt{2}) . Et de même ^{2}=3-2\sqrt{2}) . D'autre part, On a ^{3}=1^3+3*1^2*\sqrt{2}+3*(\sqrt{2})^2*1+(\sqrt{2})^3) . Donc ^{3}=1+3*\sqrt{2}+3*2+2*\sqrt{2}) . Donc ^{3}=1+5\sqrt{2}+6) . Donc ^{3}=7+5\sqrt{2}) . Et de même: ^{3}=7-5\sqrt{2}) . Coclusion: Si ^{n}=p+q\sqrt{2}) . Alors ^{n}=p-q\sqrt{2}) . Dans notre exercice: On a n=2006, p=a, et q=b. On a ^{2006}=a+b\sqrt{2}) . Donc ^{2006}=a-b\sqrt{2}) . Finalement, on a (a+b\sqrt{2})) . Donc ^{2006}*(1+\sqrt{2})^{2006}) . Donc (1+\sqrt{2}))^{2006}) . Donc ^2)^{2006}) . Donc ^{2006}) . Donc ^{2006}) . Donc 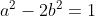 . P.S: Même dans ce niveau, je pense qu'on ne peut pas démonter ce que j'ai utiliser. On a qu'à l'admettre. | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sam 01 Mai 2010, 14:11 | |
| L'exercice courant: Calculez la somme suivante: 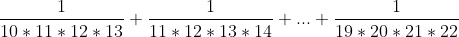 . Bonne chance.
Dernière édition par nmo le Sam 01 Mai 2010, 16:24, édité 1 fois | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sam 01 Mai 2010, 16:22 | |
| Il faut que tu ajoute le troisiéme nombre... Car on arrive pas de connaitre (المتتالية).
1/(10*12*13)+...?? | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sam 01 Mai 2010, 16:25 | |
| - M.Marjani a écrit:
- Il faut que tu ajoute le troisiéme nombre... Car on arrive pas de connaitre (المتتالية).
1/(10*12*13)+...?? Maintenant, c'est édité. J'ai oublié le quatrième nombre. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 01:45 | |
| Ma propre methode: Premiérement il parait clair qu'il ya (10 حدود) Sinon on fait (19-10)+1=10: n(final)=19 et n(initial)=10 +(n+2)+(n+3)}+\frac{1}{(n+1)+(n+2)+(n+3)+(n+4)}=\frac{1}{4n+6}+\frac{1}{4n+10}) +(n+3)+(n+4)+(n+5)}+\frac{1}{(n+3)+(n+4)+(n+5)+(n+6)}=\frac{1}{4n+14}+\frac{1}{4n+18}) 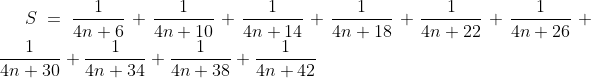 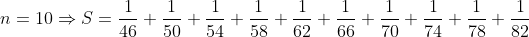 Le calcul dit que: S=0,16 donc  CQFD. | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 12:23 | |
| | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 12:58 | |
| Bonne remarque. LOL! Malheureusement, j'avais fais une faute, dés la premiére faute j'vais cru que c'est n+(n+1)+... Je vais essaie une autre fois, aprés faire un EX. | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 13:34 | |
| - nmo a écrit:
- L'exercice courant:
Calculez la somme suivante:
.
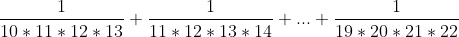Bonne chance. Remarquons tout d'abord que : (n+2)(n+3)}=-\frac{1}{2(n+1)}+\frac{1}{2(n+2)}-\frac{1}{6(n+3)}+\frac{1}{6n}\\\Leftrightarrow%20\frac{1}{n(n+1)(n+2)(n+3)}=\frac{1}{2}\begin{pmatrix}%20-\frac{1}{n+1}+\frac{1}{n+2}%20\end{pmatrix}+\frac{1}{6}\begin{pmatrix}%20-\frac{1}{n+3}+\frac{1}{n}%20\end{pmatrix}) Par conséquent : 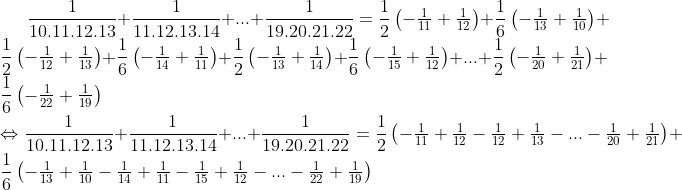 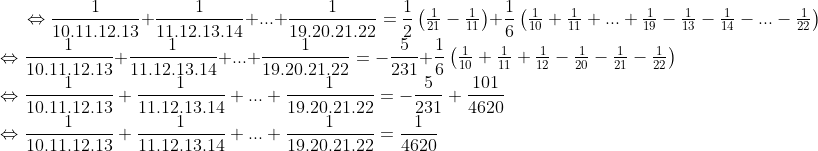 Sauf erreur. Au plaisir ! | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 16:33 | |
| Bonne réponse mizmaz, à toi de poster.
Le résultat est fort juste. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 16:54 | |
| | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 17:32 | |
| Bonsoir. Sur une table rectangulaire de dimension 2m×1m sont réparties 500 miettes de pain. Prouver que l'on peut trouver trois miettes qui déterminent un triangle d'aire inférieure à 50cm². Au plaisir ! | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 17:41 | |
| - mizmaz a écrit:
- Bonsoir.
Sur une table rectangulaire de dimension 2m×1m sont réparties 500 miettes de pain. Prouver que l'on peut trouver trois miettes qui déterminent un triangle d'aire inférieure à 50cm².
Au plaisir ! Ce n'est pas pour les troncs communs. Les probabilités sont d'un niveau supérieur. Il vaut mieux changer cet exrcice et poster un de nôtre niveau. | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 17:44 | |
| - nmo a écrit:
- mizmaz a écrit:
- Bonsoir.
Sur une table rectangulaire de dimension 2m×1m sont réparties 500 miettes de pain. Prouver que l'on peut trouver trois miettes qui déterminent un triangle d'aire inférieure à 50cm².
Au plaisir ! Ce n'est pas pour les troncs communs.
Les probabilités sont d'un niveau supérieur.
Il vaut mieux changer cet exrcice et poster un de nôtre niveau. Ce n'est pas vraiment dur pour un tronc commun. Il suffit de bien raisonner. Au plaisir ! | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 21:46 | |
| Je vais essaie aprés une Douche. | |
|
| | |
master
Maître
Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Dim 02 Mai 2010, 21:50 | |
| slt mizmaz ^^ :
on vas appliquer principe de tirroir .
alors notre table sera divisible a 200 caree et chaque carre vas avoir 10 cm dans chaque cote.
donc on appliquant notre principe puisque on a trouve les tirroirs , on aurait qu'il yen a 3 miettes dans chaques carre qui vont donner un triangle avec un air inferieur a la moitie de la surface du carre, alors c b1 vus d'apres calcul que c'etait 50 cm².
alors ? | |
|
| | |
master
Maître
Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Lun 03 Mai 2010, 13:20 | |
| alors ??? je peux poster mon exo ? | |
|
| | |
mizmaz
Maître
Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Lun 03 Mai 2010, 14:23 | |
| Oui. | |
|
| | |
master
Maître
Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Lun 03 Mai 2010, 14:46 | |
| ok donc voila prouver que si ab+1 divise a²+b² ==> a²+b²/ab+1 est un carré parfait. (a,b)£N .
amusez-vous !!!
c assez facile ... | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) | |
| |
|
| | |
| | Préparations aux olympiades de tronc commun (2009-2010) | |
|
