| | Marathon des équations fonctionnelles |  |
|
+360000 Misterayyoub kaj mima rimele expert_run az360 symizter abdelbaki.attioui Mehdi.O Sporovitch darkpseudo yasserito mizmaz King ali-mes L'enfant xyzakaria tarask nononabil nmo Othmaann Le criminelle kholoud-tetouanie MohE samia08 elhor_abdelali Othman24 majdouline imanos Bison_Fûté joystar1 oussama1305 Sylphaen pco M.Marjani Dijkschneier 40 participants |
|
| Auteur | Message |
|---|
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mar 19 Avr 2011, 09:02 Mar 19 Avr 2011, 09:02 | |
| - Dijkschneier a écrit:
- En voici une que je viens de construire :
Problème 55 : (* : une étoile, jusqu'à ** : deux étoiles)
Trouver toutes les fonctions f : IR --> IR qui vérifient : f(x-f(y))=f(x)+f(f(y))-2xf(y) Bonjour à tous. D'abord une remarque : rechercher la surjectivité est inutile puisqu'on connait une solution non surjective f(x)=x^2. Soit P(x,y) l'assertion f(x-f(y))=f(x)+f(f(y))-2xf(y) P(f(x),x) implique f(f(x))=f(0)/2+f(x)^2 P(f(x),y) peut alors s'écrire f(f(x)-f(y))=f(f(x))+f(f(y))-2f(x)f(y) = f(0)+f(x)^2+f(y)^2-2f(x)f(y) et donc f(f(x)-f(y))=f(0)+(f(x)-f(y))^2 Considérons maintenant deux cas : Cas 1 : Si f(x)=0 pour tout x, on a une soluttion Cas 2 : Si f(u) est différent de 0 pour un certain réel u, alors : P((f(f(u))-z)/(2f(u)), u) implique f(qqchose)=f(autrechose)+z et donc tout réel z peut se mettre sous la forme d'une différence f(a)-f(b) Et comme nous avons démontré que f(f(x)-f(y))=f(0)+(f(x)-f(y))^2, alors f(z)=f(0)+z^2 Et, en plongeant cela dans l'équation initiale, on trouve f(0)=0 et donc deux solutions à cette équation : f(x)=0 pour tout x f(x)=x^2 pour tout x | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mar 19 Avr 2011, 12:26 Mar 19 Avr 2011, 12:26 | |
| Bonjour pco.
Je n'attendais pas de vous que vous postiez votre réponse puisque vous l'aviez déjà fait ici : http://www.artofproblemsolving.com/Forum/viewtopic.php?f=36&t=378718&p=2092364&hilit=%22f+x+f+y+%3Df+x+f+f+y+2xf+y+%22#p2092364
J'ai retrouvé ce lien a posteriori pour savoir si ce problème n'était pas déjà connu, mais il l'est. | |
|
  | |
symizter
Débutant
 Nombre de messages : 5 Nombre de messages : 5
Age : 31
Date d'inscription : 14/04/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 29 Avr 2011, 11:51 Ven 29 Avr 2011, 11:51 | |
| Bonjour à tous,
Je souhaite ne pas dérailler le marathon, en évoquant de nouveau le probèlme posté par nmo en 07/09/2010.l'EF posée m'intéresse toujours. - Citation :
- Alors je propose:
Exercice 27:
Trouvez tous les fonctions définies de IR vers IR, et qui satisfont la relation pour tous les réels x et y:
f(x+y)=f(x)f(a-y)+f(y)f(a-x).
Et a un réel constant.
Bonne chance.
---- Je présente ma tentative :Quelque soit (x,y) dans IR² , On a : =f(x)f(a-y)+f(y)f(a-x)) ( (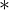 )Remarque : si a= pi/2 , la fonction f définie par : f(x)= sin(x) sera une solution. (1) pour y=a-x on a f(a)=(f(x))² +(f(a-x))² , Donc f(a)>=0 . )Remarque : si a= pi/2 , la fonction f définie par : f(x)= sin(x) sera une solution. (1) pour y=a-x on a f(a)=(f(x))² +(f(a-x))² , Donc f(a)>=0 .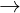 si f(a)=0, la fonction nulle est une solution. si f(a)=0, la fonction nulle est une solution. 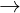 si f(a) si f(a) 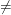 0 : ( x=y=0)( 0 : ( x=y=0)(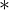 ) : f(0)= f(0)f(a)+f(0)f(a) 0= (2f(a)-1)f(0) Donc, f(0)=0 ou f(a)=1/2 A) Le premier cas: si f(0) ) : f(0)= f(0)f(a)+f(0)f(a) 0= (2f(a)-1)f(0) Donc, f(0)=0 ou f(a)=1/2 A) Le premier cas: si f(0) 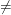 0 alors f(a)=1/2de (1) , on déduit que: (x=0) f(a)= f(0)² + (f(a))² 1/2 = ((f(0))² + 1/4 Par conséquent: ((f(0))² = 1/4 => f(0)= +- 1/2 .Supposons que f(0)= -1/2 (x=0) 0 alors f(a)=1/2de (1) , on déduit que: (x=0) f(a)= f(0)² + (f(a))² 1/2 = ((f(0))² + 1/4 Par conséquent: ((f(0))² = 1/4 => f(0)= +- 1/2 .Supposons que f(0)= -1/2 (x=0) 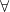 y : f(y)=f(0)f(a-y) +f(y)f(a) f(y)= -1/2 f(a-y) + 1/2 f(y)Donc : y : f(y)=f(0)f(a-y) +f(y)f(a) f(y)= -1/2 f(a-y) + 1/2 f(y)Donc : 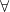 y f(y)= -f(a-y)Par conséquent y f(y)= -f(a-y)Par conséquent 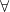 x f(x)= -f(a-x) . (y=0) : f(x)=f(x)f(a)+f(0)f(a-x) = 1/2 f(x) -1f(x+x)= f(x)f(a-x)+ f(x)f(a-x)f(2x) = 2f(x)f(a-x) = -2((f(x))² =< 0 Donc f(2x)=< 0 f(2 . x/2) =< 0Par conséquent : f(x) =< 0 f(a)=< 0 1/2 =< 0 - Contradiction - Donc, f(0)=1/2(y=0) : f(x)= f(x)f(a)+f(0)f(a-x) f(x)= 1/2 f(x) +1/2f(a-x) f(x)= f(a-x) (y=x ) : x f(x)= -f(a-x) . (y=0) : f(x)=f(x)f(a)+f(0)f(a-x) = 1/2 f(x) -1f(x+x)= f(x)f(a-x)+ f(x)f(a-x)f(2x) = 2f(x)f(a-x) = -2((f(x))² =< 0 Donc f(2x)=< 0 f(2 . x/2) =< 0Par conséquent : f(x) =< 0 f(a)=< 0 1/2 =< 0 - Contradiction - Donc, f(0)=1/2(y=0) : f(x)= f(x)f(a)+f(0)f(a-x) f(x)= 1/2 f(x) +1/2f(a-x) f(x)= f(a-x) (y=x ) : 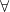 x f(2x)=2f(x)f(a-x) = 2(f(x))² >=0Donc, x f(2x)=2f(x)f(a-x) = 2(f(x))² >=0Donc, 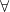 x : f(x)>=0 de (1), on déduit que: x : f(x)>=0 de (1), on déduit que: 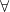 x : 1/2 = ((f(x))² + (f(x))² , donc (f(x))² = 1/4Par conséquent: x : 1/2 = ((f(x))² + (f(x))² , donc (f(x))² = 1/4Par conséquent: 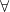 x f(x)=1/2inversement, la fonction constante f: x x f(x)=1/2inversement, la fonction constante f: x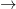 1/2 est une solution. B) le deuxième cas: - si f(0)=0( pour x=0 dans (1) ) , f(a)=f(a)² Donc, f(a)=1 ( car f(a) 1/2 est une solution. B) le deuxième cas: - si f(0)=0( pour x=0 dans (1) ) , f(a)=f(a)² Donc, f(a)=1 ( car f(a) 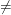 0) ( le cas f(a)=0 est déja fait) (1) : 1=f(x)²+ (f(a-x))² ( y=a) f(x+a) = f(x)f(a-a)+f(a)f(a-x) f(x+a)= f(a-x) (y=-x) f(0)=f(x)f(a+x) +f(-x)f(a+x) ( f(a-x)=f(a+x) ) 0 = f(x)f(a+x) + f(-x)f(a+x) 0=(f(x)+f(-x)) f(a+x) Maintenant, on doit nécessairement répondre aux question suivantes: - Est-ce que la fonction f est impaire ?- Est-elle périodique?- Est-elle dérivable sur IR ? Pour passer à l'équation differentiel : 0) ( le cas f(a)=0 est déja fait) (1) : 1=f(x)²+ (f(a-x))² ( y=a) f(x+a) = f(x)f(a-a)+f(a)f(a-x) f(x+a)= f(a-x) (y=-x) f(0)=f(x)f(a+x) +f(-x)f(a+x) ( f(a-x)=f(a+x) ) 0 = f(x)f(a+x) + f(-x)f(a+x) 0=(f(x)+f(-x)) f(a+x) Maintenant, on doit nécessairement répondre aux question suivantes: - Est-ce que la fonction f est impaire ?- Est-elle périodique?- Est-elle dérivable sur IR ? Pour passer à l'équation differentiel : =0 & \end{matrix}\right. ,f'(0)= C) .. .. | |
|
  | |
pco
Expert sup
 Nombre de messages : 678 Nombre de messages : 678
Date d'inscription : 06/06/2006
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 30 Avr 2011, 07:05 Sam 30 Avr 2011, 07:05 | |
| - symizter a écrit:
-
...
Maintenant, on doit nécessairement répondre aux question suivantes:
- Est-ce que la fonction f est impaire ?
- Est-elle périodique?
- Est-elle dérivable sur IR ?
Pour passer à l'équation differentiel :
=0 & \end{matrix}\right. ,f'(0)= C)
.. Bonjour symizter, Si a est non nul, on a au moins la solution f(x)=sin(h(x)) avec h(x) vérifiant h(x+y)=h(x)+h(y) et h(a)=pi/2 Et donc une infinité de solutions non continues, et donc évidemment non dérivables. Il n'y a donc pas moyen de résoudre ce genre de problèmes via une équation différentielle. Ces problèmes (diverses variations de l'équation de d'Alembert) ne sont à mon avis pas sérieusement résolubles sans au moins la condition de continuité. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 00:33 Lun 15 Aoû 2011, 00:33 | |
| Exercice 28 :
Trouver toutes les fonctions f : IR -> IR qui vérifient l'équation fonctionnelle : f(xf(x)+f(y)) = f(x)^2 + y. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 03:11 Lun 15 Aoû 2011, 03:11 | |
| - az360 a écrit:
- Exercice 28 :
Trouver toutes les fonctions f : IR -> IR qui vérifient l'équation fonctionnelle : f(xf(x)+f(y)) = f(x)^2 + y. Solution pour 28:pour x=0 ===>f(f(y))=y +f(0)^2===>fof est bijective ===> f est bijective y=x=0===>f(f(0))=f(0)^2=0 ==>f(0)=0 Puisque f est bijective on pose: f(a)=x et y=0 Donc f(af(a))=a^2=f(a)^2 On conclut donc que f(x)=x ou f(x)=-x Réciproquement on voit que c'est juste. CQFD | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 03:14 Lun 15 Aoû 2011, 03:14 | |
| - expert_run a écrit:
- az360 a écrit:
- Exercice 28 :
Trouver toutes les fonctions f : IR -> IR qui vérifient l'équation fonctionnelle : f(xf(x)+f(y)) = f(x)^2 + y. Solution pour 28:
pour x=0 ===>f(f(y))=y +f(0)^2===>fof est bijective ===> f est bijective
y=x=0===>f(f(0))=f(0)^2=0 ==>f(0)=0
Puisque f est bijective on pose:
f(a)=x et y=0
Donc f(af(a))=a^2=f(a)^2
On conclut donc que f(x)=x ou f(x)=-x
Réciproquement on voit que c'est juste.
CQFD Ouiii . | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 03:45 Lun 15 Aoû 2011, 03:45 | |
|
Dernière édition par expert_run le Jeu 18 Aoû 2011, 16:39, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 13:32 Lun 15 Aoû 2011, 13:32 | |
| - expert_run a écrit:
- az360 a écrit:
- Exercice 28 :
Trouver toutes les fonctions f : IR -> IR qui vérifient l'équation fonctionnelle : f(xf(x)+f(y)) = f(x)^2 + y. Solution pour 28:
pour x=0 ===>f(f(y))=y +f(0)^2===>fof est bijective ===> f est bijective
y=x=0===>f(f(0))=f(0)^2=0 ==>f(0)=0Puisque f est bijective on pose:
f(a)=x et y=0
Donc f(af(a))=a^2=f(a)^2
On conclut donc que f(x)=x ou f(x)=-xRéciproquement on voit que c'est juste.
CQFD Ce qui est en rouge est faux | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 13:41 Lun 15 Aoû 2011, 13:41 | |
| Solution au problème 28:- Spoiler:
Soit f une solution éventuelle de l'EF:
Soit P'x,y) l'assertion f(xf(x)+f(y))=(f(x))²+y
P(0,y) : f(f(y))=(f(0))²+y ainsi f est bijective.
Ainsi il existe un a tel que f(a)=0
P(a,a):f(0)=a => f(f(0))=0
P(0,0):0=f(f(0))=(f(0))² et ainsi f(0)=0
Ainsi on obtient pour tout x de IR f(f(x))=x => (1)
P(x,0) :f(xf(x))=(f(x))² => (2)
D'après (1) et (2) nous avons f(f(1))=1 et f(f(1))=(f(1))² et ainsi f(1)=1 ou bien f(1)=-1.
-Cas 1: f(1)=1:
P(1,f(y))f(1+f(f(y))=1+f(y)=f(1+y).
Puisque nous avons f(xf(x))=(f(x))² alors d'après le changement x->f(x) nous avons f(xf(x))=(f(x))²=x².
Ainsi :
(f(x+1))²=(f(x)+1)²<=>(x+1)²=(f(x))²+2f(x)+1<=>x²+2x+1=x²+2f(x)+1<=> f(x) =x pour tout x £ IR.
-Cas 2 : f(1)=-1:
Il se traite analogiquement puisque nous retrouvons f(y-1)=f(y)+1 et en procédant de la même façon on trouve f(x)=-x pour tout x £ IR.
Réciproquement, f(x)=x et f(x)=-x sont bien solutions à l'EF.
| |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 15 Aoû 2011, 15:25 Lun 15 Aoû 2011, 15:25 | |
| - Mehdi.O a écrit:
- expert_run a écrit:
- az360 a écrit:
- Exercice 28 :
Trouver toutes les fonctions f : IR -> IR qui vérifient l'équation fonctionnelle : f(xf(x)+f(y)) = f(x)^2 + y. Solution pour 28:
pour x=0 ===>f(f(y))=y +f(0)^2===>fof est bijective ===> f est bijective
y=x=0===>f(f(0))=f(0)^2=0 ==>f(0)=0Puisque f est bijective on pose:
f(a)=x et y=0
Donc f(af(a))=a^2=f(a)^2
On conclut donc que f(x)=x ou f(x)=-xRéciproquement on voit que c'est juste.
CQFD Ce qui est en rouge est faux Ah oui quand j'étais entrain de recopier sur le forum j'ai oublier de mentionner bcp de choses . Alors puisque f est bijective il existe z€IR tel que f(z)=0 ===>f(f(x))=x C'est là d'où j'ai conclu la première phrase en rouge Pour la deuxième j'ai utiliser f(f(x))=x qui donne directement les résultats. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 16:20 Jeu 18 Aoû 2011, 16:20 | |
| @ expert-run: Ton problème est un P6 d'un ancien IMO, tu pourrais changer le problème si ça en te dérange pas  ? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 16:38 Jeu 18 Aoû 2011, 16:38 | |
| - Mehdi.O a écrit:
- @ expert-run: Ton problème est un P6 d'un ancien IMO, tu pourrais changer le problème si ça en te dérange pas
 ? ? Ok .Avec plaisir. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 17:10 Jeu 18 Aoû 2011, 17:10 | |
| Problème 29:Trouver toutes les fonction f: IR--->IR tel que: =\max\{f(x+y),f(x)&space;f(y)\}) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 20:18 Jeu 18 Aoû 2011, 20:18 | |
| Solution au problème 29:- Spoiler:
La condition du problème est équivalente au fait que : \in&space;\mathbb{R}^{2}:f(xy)\geq&space;f(x)f(y)|f(xy)\geq&space;f(x+y)) . Alors on pose P(x,y) l'assertion f(xy)>=f(x+y) et Q(x,y) l'assertion f(xy)>=f(x)f(y). P(x,0) : Pour tout x £ IR f(x)<=f(0). Q(0,0) : 0<=f(0)<=1. Q(x,0): Pour tout x £ IR f(x)<=1. Q(1,1) : f(1)(1-f(1)) >=0 et ainsi f(1)>=0. Q(x,1) f(x)(1-f(1))>=0 et ainsi pour tout x de IR 0<= f(x) <=1. P(x,-x) f(-x²) >=f(0) mais puisque pour tout x de IR nous avons f(-x²) <= f(0), on en déduit que f est constante sur IR-. i.e : pour tout x £ IR- f(x)=f(0). Maintenant considérons y et z deux réels négatifs( il est bien clair que y+z <=0) P(y,z) f((yz)) >=f(y+z)=f(0) >= f(yz). Mais pusique yz £ IR+, alors pour tout x de IR+ f(x)=f(0). Ainsi on en déduit que pour tout x £ IR f(x)=f(0). Synthèse : La seule solution à l'EF est f(x)= c où c est un réel compris entre 0 et 1. Réciproquement elle satisfait l'EF. Sauf erreur  ..
| |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 22:41 Jeu 18 Aoû 2011, 22:41 | |
| Oui c'est juste à toi de poster. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 22:49 Jeu 18 Aoû 2011, 22:49 | |
| Problème 30:
Trouver toutes les fonctions f:IR->IR tel que pour tout (x,y) £ IR² nous avons :
(x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)). | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 23:39 Jeu 18 Aoû 2011, 23:39 | |
| - Mehdi.O a écrit:
- Problème 30:
Trouver toutes les fonctions f:IR->IR tel que pour tout (x,y) £ IR² nous avons :
(x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)). - Spoiler:
On pose P(x,y) l'assertion (x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)) (*)
Donc:
P(1;0):f(0)=2f(f(0))
Soit y=/=0 donc:
P(0;y): yf(y)+yf(f(0))=yf(f(y)) <==>f(y)+f(f(0))=f(f(y))
Alors f(y)+f(0)/2=f(f(y))
Donc l'eq.fct <==>(x+y)f(y)+yf(x)+yf(0)/2=( 2x+y)( f(y)+f(0)/2)
<==> xf(y) +xf(0)-yf(x)=0
Alors:
P(1;1): f(0)=0
Donc yf(x)=xf(y) .Pour y=1 on a : f(x)=xf(1)
Alors f(x)=ax .Il nous reste à calculer les valeurs de a.
On remplace f(x) par ax dans (*)
Donc a=0 ou a=1
Synthèse: l'EF admet deux solutions : f(x)=0 et f(x)=x
Sauf erreur.
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 23:41 Jeu 18 Aoû 2011, 23:41 | |
| - expert_run a écrit:
- Mehdi.O a écrit:
- Problème 30:
Trouver toutes les fonctions f:IR->IR tel que pour tout (x,y) £ IR² nous avons :
(x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)). - Spoiler:
On pose P(x,y) l'assertion (x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)) (*)
Donc:
P(1;0):f(0)=2f(f(0))
Soit y=/=0 donc:
P(0;y): yf(y)+yf(f(0))=yf(f(y)) <==>f(y)+f(f(0))=f(f(y))
Alors f(y)+f(0)/2=f(f(y))
Donc l'eq.fct <==>(x+y)f(y)+yf(x)+yf(0)/2=( 2x+y)( f(y)+f(0)/2)
<==> xf(y) +xf(0)-yf(x)=0
Alors:
P(1;1): f(0)=0
Donc yf(x)=xf(y) .Pour y=1 on a : f(x)=xf(1)
Alors f(x)=ax .Il nous reste à calculer les valeurs de a.
On remplace f(x) par ax dans (*)
Donc a=0 ou a=1
Synthèse: l'EF admet deux solutions : f(x)=0 et f(x)=x
Sauf erreur.
Oui c'est ça bien joué  . A toi de poster un exo  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 23:46 Jeu 18 Aoû 2011, 23:46 | |
| Problème 31:
Trouver toutes les fonctions strictement croissantes f:IN*--->IN* :
i)f(2)=2
ii) si le PGCD(m;n)=1 ;f(m.n)=f(m)f(n)
Dernière édition par expert_run le Ven 19 Aoû 2011, 22:41, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 11:39 Ven 19 Aoû 2011, 11:39 | |
| Solution au problème 31:( à vérifier ..) - Spoiler:
On note _{n&space;\in&space;\mathbb{N}}) la suite des nombres premiers stricitement positifs, et on assume que 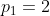 . On prouve alors par récurrence immédiate que : \in&space;\mathbb{N}^{n})(\forall&space;(\alpha&space;_1,\alpha&space;_2,..,\alpha_&space;n)\in&space;\mathbb{N}^{n}):&space;f(\prod&space;_{i=1}^{n}p_i^{\alpha&space;_i})=\prod_{i=1}^{n}f(p_i^{\alpha&space;_i})) . Ce qui est clairement vrai, vu que les nombres premiers et leurs puissances sont premiers entre eux deux à deux. Et d'après la décomposition de chaque entier en facteurs de nombres premiers, alors on peut calculer aisément son image, si nous avons en notre possesion les images des nombres premiers et leurs puissances. A ce terme on construit une suite _{n&space;\in&space;\mathbb{N}}) qui associe chaque nombre premier à son image par f, et qui est définie comme suit : =f\(2)=2\&space;&&space;\forall&space;n&space;\in&space;\mathbb{N}&space;&a_n=&space;f(p_n)&space;\end{cases}) . On peut également assumer qu'une telle fonction qui satisfait ces conditions vérifie le fait quer : (\forall&space;p\in&space;\mathbb{P}):f(p^{q})=(f(p))^{q}) . A ce terme nous avons suffisement de conditions pour construire une telle fonction ( par exemple l'identité ..) Mais déterminer toutes les fonctions est impossible vu qu'il en existe une infinité qui satisfaisent les conditions suivantes . Sauf erreur 
| |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 14:46 Ven 19 Aoû 2011, 14:46 | |
| expert-run je pense que t'as oublie d'ajoute la condition f strictement croissante...c'est un classique bien connnu et la seule solution est l'identité...
Pour Mehdi-o ta solution n'est pas bonne... | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 14:49 Ven 19 Aoû 2011, 14:49 | |
| Je me disais qu'il manquait un truc dans le problème  . Merci d'éditer ton problème expert-run pour que je puisse rectifier ma solution. | |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 17:23 Ven 19 Aoû 2011, 17:23 | |
| bjr bon je propose une solution pour le probleme 31 ,et j ajoute que f est strictement croissante.
la fonction Ide est bien une solution...prouvons que c'est la seule possible.
par réccurence, f(1)=1,f(2)=2
soit n un entier on suppose que pour tout p inferieure ou egale á n on a : f(p)=p
prouvons que f(n+1)=n+1
1) si n+1 n'est pas premier alors il existe q,k inferieur á n tel que: qk=n+1.
d'ou f(n+1)=f(qk)=f(q)f(k)=qk (par hypothese de reccurence forte)
2) si maintenant n+1 premier alors n+2 est impaire ainsi il existe d=<n tel que n+2=2d
d'ou f(n+2)=f(2)f(d)=2d=n+1..or f est strictement croissante donc ;
f(n)<f(n+1)<f(n+2) d'ou f(n+1)=n+1..ce qui achéve la demonstration.
Réciproquement la fonction Ide est bien une solution du probleme. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 18:09 Ven 19 Aoû 2011, 18:09 | |
| @rimele : A toi de proposer u nouveau problème  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  | |
| |
|
  | |
| | Marathon des équations fonctionnelles |  |
|
