| | Marathon des équations fonctionnelles |  |
|
+360000 Misterayyoub kaj mima rimele expert_run az360 symizter abdelbaki.attioui Mehdi.O Sporovitch darkpseudo yasserito mizmaz King ali-mes L'enfant xyzakaria tarask nononabil nmo Othmaann Le criminelle kholoud-tetouanie MohE samia08 elhor_abdelali Othman24 majdouline imanos Bison_Fûté joystar1 oussama1305 Sylphaen pco M.Marjani Dijkschneier 40 participants |
|
| Auteur | Message |
|---|
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 22:41 Jeu 18 Aoû 2011, 22:41 | |
| Oui c'est juste à toi de poster. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 22:49 Jeu 18 Aoû 2011, 22:49 | |
| Problème 30:
Trouver toutes les fonctions f:IR->IR tel que pour tout (x,y) £ IR² nous avons :
(x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)). | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 23:39 Jeu 18 Aoû 2011, 23:39 | |
| - Mehdi.O a écrit:
- Problème 30:
Trouver toutes les fonctions f:IR->IR tel que pour tout (x,y) £ IR² nous avons :
(x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)). - Spoiler:
On pose P(x,y) l'assertion (x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)) (*)
Donc:
P(1;0):f(0)=2f(f(0))
Soit y=/=0 donc:
P(0;y): yf(y)+yf(f(0))=yf(f(y)) <==>f(y)+f(f(0))=f(f(y))
Alors f(y)+f(0)/2=f(f(y))
Donc l'eq.fct <==>(x+y)f(y)+yf(x)+yf(0)/2=( 2x+y)( f(y)+f(0)/2)
<==> xf(y) +xf(0)-yf(x)=0
Alors:
P(1;1): f(0)=0
Donc yf(x)=xf(y) .Pour y=1 on a : f(x)=xf(1)
Alors f(x)=ax .Il nous reste à calculer les valeurs de a.
On remplace f(x) par ax dans (*)
Donc a=0 ou a=1
Synthèse: l'EF admet deux solutions : f(x)=0 et f(x)=x
Sauf erreur.
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 23:41 Jeu 18 Aoû 2011, 23:41 | |
| - expert_run a écrit:
- Mehdi.O a écrit:
- Problème 30:
Trouver toutes les fonctions f:IR->IR tel que pour tout (x,y) £ IR² nous avons :
(x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)). - Spoiler:
On pose P(x,y) l'assertion (x+y)f(y) + yf(f(x)) = (2x+y)f(f(y)) (*)
Donc:
P(1;0):f(0)=2f(f(0))
Soit y=/=0 donc:
P(0;y): yf(y)+yf(f(0))=yf(f(y)) <==>f(y)+f(f(0))=f(f(y))
Alors f(y)+f(0)/2=f(f(y))
Donc l'eq.fct <==>(x+y)f(y)+yf(x)+yf(0)/2=( 2x+y)( f(y)+f(0)/2)
<==> xf(y) +xf(0)-yf(x)=0
Alors:
P(1;1): f(0)=0
Donc yf(x)=xf(y) .Pour y=1 on a : f(x)=xf(1)
Alors f(x)=ax .Il nous reste à calculer les valeurs de a.
On remplace f(x) par ax dans (*)
Donc a=0 ou a=1
Synthèse: l'EF admet deux solutions : f(x)=0 et f(x)=x
Sauf erreur.
Oui c'est ça bien joué  . A toi de poster un exo  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Jeu 18 Aoû 2011, 23:46 Jeu 18 Aoû 2011, 23:46 | |
| Problème 31:
Trouver toutes les fonctions strictement croissantes f:IN*--->IN* :
i)f(2)=2
ii) si le PGCD(m;n)=1 ;f(m.n)=f(m)f(n)
Dernière édition par expert_run le Ven 19 Aoû 2011, 22:41, édité 1 fois | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 11:39 Ven 19 Aoû 2011, 11:39 | |
| Solution au problème 31:( à vérifier ..) - Spoiler:
On note _{n&space;\in&space;\mathbb{N}}) la suite des nombres premiers stricitement positifs, et on assume que 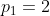 . On prouve alors par récurrence immédiate que : \in&space;\mathbb{N}^{n})(\forall&space;(\alpha&space;_1,\alpha&space;_2,..,\alpha_&space;n)\in&space;\mathbb{N}^{n}):&space;f(\prod&space;_{i=1}^{n}p_i^{\alpha&space;_i})=\prod_{i=1}^{n}f(p_i^{\alpha&space;_i})) . Ce qui est clairement vrai, vu que les nombres premiers et leurs puissances sont premiers entre eux deux à deux. Et d'après la décomposition de chaque entier en facteurs de nombres premiers, alors on peut calculer aisément son image, si nous avons en notre possesion les images des nombres premiers et leurs puissances. A ce terme on construit une suite _{n&space;\in&space;\mathbb{N}}) qui associe chaque nombre premier à son image par f, et qui est définie comme suit : =f\(2)=2\&space;&&space;\forall&space;n&space;\in&space;\mathbb{N}&space;&a_n=&space;f(p_n)&space;\end{cases}) . On peut également assumer qu'une telle fonction qui satisfait ces conditions vérifie le fait quer : (\forall&space;p\in&space;\mathbb{P}):f(p^{q})=(f(p))^{q}) . A ce terme nous avons suffisement de conditions pour construire une telle fonction ( par exemple l'identité ..) Mais déterminer toutes les fonctions est impossible vu qu'il en existe une infinité qui satisfaisent les conditions suivantes . Sauf erreur 
| |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 14:46 Ven 19 Aoû 2011, 14:46 | |
| expert-run je pense que t'as oublie d'ajoute la condition f strictement croissante...c'est un classique bien connnu et la seule solution est l'identité...
Pour Mehdi-o ta solution n'est pas bonne... | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 14:49 Ven 19 Aoû 2011, 14:49 | |
| Je me disais qu'il manquait un truc dans le problème  . Merci d'éditer ton problème expert-run pour que je puisse rectifier ma solution. | |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 17:23 Ven 19 Aoû 2011, 17:23 | |
| bjr bon je propose une solution pour le probleme 31 ,et j ajoute que f est strictement croissante.
la fonction Ide est bien une solution...prouvons que c'est la seule possible.
par réccurence, f(1)=1,f(2)=2
soit n un entier on suppose que pour tout p inferieure ou egale á n on a : f(p)=p
prouvons que f(n+1)=n+1
1) si n+1 n'est pas premier alors il existe q,k inferieur á n tel que: qk=n+1.
d'ou f(n+1)=f(qk)=f(q)f(k)=qk (par hypothese de reccurence forte)
2) si maintenant n+1 premier alors n+2 est impaire ainsi il existe d=<n tel que n+2=2d
d'ou f(n+2)=f(2)f(d)=2d=n+1..or f est strictement croissante donc ;
f(n)<f(n+1)<f(n+2) d'ou f(n+1)=n+1..ce qui achéve la demonstration.
Réciproquement la fonction Ide est bien une solution du probleme. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Ven 19 Aoû 2011, 18:09 Ven 19 Aoû 2011, 18:09 | |
| @rimele : A toi de proposer u nouveau problème  | |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Sam 20 Aoû 2011, 17:19 Sam 20 Aoû 2011, 17:19 | |
| D'accord,je propose ce probleme.
Trouver toutes les fonctions continue de IR vers IR telles que:
pour tout x de IR:
f(x+2)-7f(x+1)+10f(x)=0 | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 22 Aoû 2011, 04:34 Lun 22 Aoû 2011, 04:34 | |
| Déjà posté au forum. Elle a une infinité de solutions et ce n'est guére facile à montrer.
Je t'invite à poster une autre. | |
|
  | |
rimele
Féru
 Nombre de messages : 36 Nombre de messages : 36
Age : 31
Date d'inscription : 19/08/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 22 Aoû 2011, 21:01 Lun 22 Aoû 2011, 21:01 | |
| d'accord je propose un autre probléme:
trouver toutes les fonctions f:IR-->IR TQ:
f(x^2(z^2+1)+f(y)(z+1))=1-f(z)(x^2+f(y))-z((z+1)x^2+2f(y))
elle n'est pas jolie mais bon... | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 22 Aoû 2011, 23:05 Lun 22 Aoû 2011, 23:05 | |
| Solution au problème 32:- Spoiler:
Soit P(x,y,z) l'assertion : +f(y)(z+1))=1-f(z)(x^2+f(y))-z((z+1)x^2+2f(y))) . P(0,y,-1) : :f(y)(2-f(-1))=f(0)-1) . Ainsi si f(-1) est différent de 2, on obtient le fait que f est constante, réciproquement celle-ci en satisfait pas l'EF. Ainsi f(-1)=2 et on obtient directement f(0)=1. P(0,0,0) : =0) . P(x,1,0) : :f(x^2)=1-x^2) . Ainsi pour tout x de IR + f(x)=1-x. P(x,1,x) et en tenant compte du fait que x²(x²+1) £ IR+, on a : )=1-f(x)x^2-x^3(x+1)\Leftrightarrow&space;1-x^4-x^2=1-f(x)x^2-x^4-x^3\Leftrightarrow&space;(\forall&space;x\in&space;\mathbb{R}^{*})f(x)=1-x) . Mais puisque f(0)=1=1-0 alors pour tout x de IR f(x)=1-x. Réciproquement cette fonction vérifie bien l'EF.
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Lun 22 Aoû 2011, 23:15 Lun 22 Aoû 2011, 23:15 | |
| Problème 33:Trouver toutes les fonctions 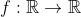 t.q pour tout x,y de IR nous avons : )+y+f(x)=f(x+f(y))+yf(x)) | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 00:02 Mer 24 Aoû 2011, 00:02 | |
| Solution 33:Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)+y=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 pour x=/=0. Puisque f(0)=0 on obtient alors
f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 pour tout x de IR , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement car on a bien x+1 se différe de x, donc f'(x+1)=lim(x-->x+1)[f(x)-f(x+1)]/[x-(x+1)]=1. Dérivable sur un point donc continue sur ce même point. Ou sans Cauchy... dérivé constante <=> fonction originale de la forme ax+b et a,b fixes et récoproquement a'=1 et b=0.
Réciproquement, f(x)=x vérifie les données et elle est la seule.
Dernière édition par M.Marjani le Mer 24 Aoû 2011, 05:32, édité 2 fois (Raison : Réctifier une légére faute de frappe.) | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 02:48 Mer 24 Aoû 2011, 02:48 | |
| - M.Marjani a écrit:
- Solution 33:
Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR. De plus si c=/=0 alors c=t(f(x)-1) => f(x)=/=1, ce qui est impossible puisque la fonction f(x)=1 répond aux données.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 si x est différent de 0. Puisque f(0)=0 on obtient alors f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement.
Réciproquement, f(x)=x et f(x)=1 vérifient les données et sont les seules. Je n'ai lu que la première ligne, et je suis désolé pour l'effort que tu as fait, mais tu as résolu une autre EF je crois, dans RHS y a : f(xf(y))+f(x) +y, tu as oublié le "y" | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 03:02 Mer 24 Aoû 2011, 03:02 | |
| - Mehdi.O a écrit:
- M.Marjani a écrit:
- Solution 33:
Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR. De plus si c=/=0 alors c=t(f(x)-1) => f(x)=/=1, ce qui est impossible puisque la fonction f(x)=1 répond aux données.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 si x est différent de 0. Puisque f(0)=0 on obtient alors f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement.
Réciproquement, f(x)=x et f(x)=1 vérifient les données et sont les seules. Je n'ai lu que la première ligne, et je suis désolé pour l'effort que tu as fait, mais tu as résolu une autre EF je crois, dans RHS y a : f(xf(y))+f(x) +y, tu as oublié le "y" Je pense qu'il fallait lire tout, ce n'est qu'une faute d'inattention!  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 03:16 Mer 24 Aoû 2011, 03:16 | |
| - M.Marjani a écrit:
- Solution 33:
Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR. De plus si c=/=0 alors c=t(f(x)-1) => f(x)=/=1, ce qui est impossible puisque la fonction f(x)=1 répond aux données.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 si x est différent de 0. Puisque f(0)=0 on obtient alors f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement.
Réciproquement, f(x)=x et f(x)=1 vérifient les données et sont les seules. Ok, oui désolé je me suis précipité. Mais dès ce passage on ne peut rien déduire, déjà je ne sais pas à ce que refère " la première" mais de toute façon on a un manque d'hypothèses pour dire que la fonction est solution de l'équation de Cauchy. Alors merci bien de rectifier  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 03:37 Mer 24 Aoû 2011, 03:37 | |
| - Mehdi.O a écrit:
- M.Marjani a écrit:
- Solution 33:
Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR. De plus si c=/=0 alors c=t(f(x)-1) => f(x)=/=1, ce qui est impossible puisque la fonction f(x)=1 répond aux données.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 si x est différent de 0. Puisque f(0)=0 on obtient alors f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement.
Réciproquement, f(x)=x et f(x)=1 vérifient les données et sont les seules. Ok, oui désolé je me suis précipité.
Mais dès ce passage on ne peut rien déduire, déjà je ne sais pas à ce que refère " la première" mais de toute façon on a un manque d'hypothèses pour dire que la fonction est solution de l'équation de Cauchy.
Alors merci bien de rectifier  De continuité, je crois ? | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 03:40 Mer 24 Aoû 2011, 03:40 | |
| - Mehdi.O a écrit:
- M.Marjani a écrit:
- Solution 33:
Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR. De plus si c=/=0 alors c=t(f(x)-1) => f(x)=/=1, ce qui est impossible puisque la fonction f(x)=1 répond aux données.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 si x est différent de 0. Puisque f(0)=0 on obtient alors f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement.
Réciproquement, f(x)=x et f(x)=1 vérifient les données et sont les seules. Ok, oui désolé je me suis précipité.
Mais dès ce passage on ne peut rien déduire, déjà je ne sais pas à ce que refère " la première" mais de toute façon on a un manque d'hypothèses pour dire que la fonction est solution de l'équation de Cauchy.
Alors merci bien de rectifier  Trés facile de les trouver. * la continuité en un point : utiliser f(x+1)-f(x)=1 alors elle est dérivable en x_0=1. * être majorée ou minorée sur un intervalle: choisir un intervalle et montrer qu'elle minorée. * être monotone sur un intervalle: évident. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 03:44 Mer 24 Aoû 2011, 03:44 | |
| - M.Marjani a écrit:
- Mehdi.O a écrit:
- M.Marjani a écrit:
- Solution 33:
Soit f une fonction qui vérifie les données. Et soit P(x,y) l'assertion f(xf(y))+f(x)=f(x+f(y)+yf(x), posant c=f(0), a=f(1).
P(0,y): f(f(y))=c(2-y)+y (*) et soit t de IR tel que f(t)=0. Par l'assertion P(t,t): c+t=f(t)=0 on aura c=-t. Et par l'assertion P(x,t): c+t=tf(x) on aura c=t(f(x)-1) <=> cf(x)=0
Si c est différent de 0 alors f(x)=0 cela est impossible car la fonction f(x)=0 ne répond pas aux données. Donc c=0 alors (*) devient f(f(x))=x pour tout x de IR. De plus si c=/=0 alors c=t(f(x)-1) => f(x)=/=1, ce qui est impossible puisque la fonction f(x)=1 répond aux données.
P(y,1): 2y-ay+a=f(1+f(y)) (**) et P(x,1):f(ax)+1=f(x+a) (***). Or on a f(f(a+x))=a+x=f(f(ax)+1) et par (**) on aura f(f(ax)+1)=2ax+a-a²x donc x(2a-1-a²)=0 => a=1 si x est différent de 0. Puisque f(0)=0 on obtient alors f(x)+f(1)=f(x+1) et f(f(x)+1)=x+1 , la premiére est l'E.F de Cauchy qui a pour solution f(x)=a'x avec a'=1 réciproquement.
Réciproquement, f(x)=x et f(x)=1 vérifient les données et sont les seules. Ok, oui désolé je me suis précipité.
Mais dès ce passage on ne peut rien déduire, déjà je ne sais pas à ce que refère " la première" mais de toute façon on a un manque d'hypothèses pour dire que la fonction est solution de l'équation de Cauchy.
Alors merci bien de rectifier 
Trés facile de les trouver.
* la continuité en un point : utiliser f(x+1)-f(x)=1 alors elle est dérivable en x_0=1.
* être majorée ou minorée sur un intervalle: choisir un intervalle et montrer qu'elle minorée.
* être monotone sur un intervalle: évident. Hein ?! Ca prouve rien ce que tu avances, désolé mais tu ne peux rien prouver, essaies de trouver une autre méthode. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 04:09 Mer 24 Aoû 2011, 04:09 | |
| - Mehdi.O a écrit:
- Hein ?!
Desolé mais tu peux rien prouvé. Jette un cline d'oeil ici pour qu'on se met d'accord sur les conditions que j'ai avancé: http://fr.wikipedia.org/wiki/%C3%89quation_fonctionnelle_de_Cauchy Puis donc on a besoin que de la continuité en un point pour prouver la linéaireté de la fonction sur IR. On a bien x+1 se différe de x, donc f'(x+1)=lim(x-->x+1)[f(x)-f(x+1)]/[x-(x+1)]=1. Dérivable sur un point donc continue sur ce même point. Ou sans Cauchy... dérivé constante <=> fonction originale de la forme ax+b a,b fixes. | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 04:22 Mer 24 Aoû 2011, 04:22 | |
| - M.Marjani a écrit:
- Mehdi.O a écrit:
- Hein ?!
Desolé mais tu peux rien prouvé.
Jette un cline d'oeil ici pour qu'on se met d'accord sur les conditions que j'ai avancé:
http://fr.wikipedia.org/wiki/%C3%89quation_fonctionnelle_de_Cauchy
Puis donc on a besoin que de la continuité en un point pour prouver la linéaireté de la fonction sur IR.
On a bien x+1 se différe de x, donc f'(x+1)=lim(x-->x+1)[f(x)-f(x+1)]/[x-(x+1)]=1. Dérivable sur un point donc continue sur ce même point. Ou sans Cauchy... dérivé constante <=> fonction originale de la forme ax+b a,b fixes. Bonsoir Si marjani , j'ai pas lu ta solution mais je crois qu'il ya quelque chose qui cloche sur le truc ecris en gras , est ce qu'il s'agit d'une derivation ou d'une continuité ou d'un mélange ^o) ? | |
|
  | |
Misterayyoub
Maître
 Nombre de messages : 139 Nombre de messages : 139
Age : 30
Date d'inscription : 26/02/2011
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  Mer 24 Aoû 2011, 04:37 Mer 24 Aoû 2011, 04:37 | |
| Solution 33Bon , je propose cette solution , elle est un peu longue mais bon  Posons P(x;y) l'assertion tel que : f(xf(y))+f(x)+y=f(x+f(y)+yf(x) P(0,y) : f(f(y))=y(1-f(0)) +2f(0) -Cas 1 : f(0)=1 donc pour tout x x de IR f(f(x))=2 P(0,0): f(2)=2 P(1,1) f(1)=1 donc 1=f(f(1))=f(1)=2 contradiction donc f(0) est differente de 1 et donc f est bijective soit il existe un c £ IR t.q : f(c)=0 .P(x,c) : c(f(x)-1)=f(0) si c est différent de 0 donc f est constante celle ci ne répond po à la question donc c=0 et ainsi f(0)=0 ce qui donne f(f(x))=x pour tout x de IR P(x,f(y)) : f(xy)+f(x)+f(y)=f(x+y)+f(x)f(y) d'autre part il existe un a de IR t.q f(a)=1 on note Q(x,y) l'assertion f(xy)+f(x)+f(y)=f(x+y)+f(x)f(y) Q(2,2) : f(2)=0 ou f(2)=2 Q(1,1) dans les 2 cas on a f(1)=1 Q(x,1) f(x+1)=f(x)+1 Q(x+1,y): f(xy+y)-f(y)=f(x+y)+fx)f(y)-f(x)-f(y) ainsi f(xy+y)-f(y)=f(xy) ainsi f(x+y)=f(x)+f(y) pr tt x,y de IR et ainsi f(x)f(xy)=f(xy) pr tt x,y de IR ces 2 conditions donnennt bien évidemment f(x)=x CQFD  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Marathon des équations fonctionnelles Sujet: Re: Marathon des équations fonctionnelles  | |
| |
|
  | |
| | Marathon des équations fonctionnelles |  |
|
