| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
majdouline
Expert sup
 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Ven 20 Aoû 2010, 01:54 | |
| solution du problème 8: - Spoiler:
on a :  ainsi on doit prouver:   Ce qui est clairement vrai par Am-Gm, Am-Gm, schur
problème9:soit a,b,c>0, prouver que:  | |
|
| | |
imanos
Féru
Nombre de messages : 66
Age : 30
Date d'inscription : 09/02/2010
| | Sujet: Re: Le marathon des inégalités: Ven 20 Aoû 2010, 22:01 | |
| Salut SOlution du probleme 9 : - Spoiler:
trop joli le probleme  supposons que a+b+c=1  ce qui est clairement vrai CQFD [spoiler/]
Problem 10:SOIent a,b,c des réels positifs tels que xy+xz+yz+xyz=4 MQ x+y+z>= xy+xz+yz | |
|
| | |
Sylphaen
Expert sup
 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Ven 20 Aoû 2010, 22:31 | |
| Problème 10 : - Spoiler:
En utilisant la substitution : 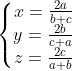 Le problème de vient équivalent à :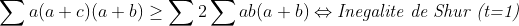 
Problème 11: a,b,c sont des réels strictement positifs tels que : 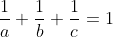 Montrer que :  | |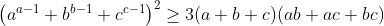
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Ven 20 Aoû 2010, 22:32 | |
| - Citation :
- Problème 11: a,b,c sont des réels strictement positifs tels que :
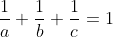
Montrer que :
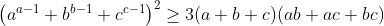Solution 10:- Spoiler:
( a,b,c) > 0 Et 1/a + 1/b + 1/c = 1 Donc (a,b,c)>1 Et abc = ab+bc+ac >= a+b+cOn sait que: (a^{a-1}+b^{b-1}+c^{c-1})² >= 3(a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1})
Il suffit donc de montrer que a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1} - abc(a+b+c) >= 0
<=>  Chose qui est vrai, En supposant a>=b>=c, donc a^a.b^b+a^a.c^c+b^b.c^c >= b^{a+b} + c^(a+c) + c^{b+c} >= (abc)^3 >= (abc)²(a+b+c)Sauf error
EDIT: Faute de frappe.
Dernière édition par M.Marjani le Sam 21 Aoû 2010, 22:08, édité 3 fois | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Ven 20 Aoû 2010, 23:54 | |
| - M.Marjani a écrit:
- imanos a écrit:
- Salut
SOlution du probleme 9 :
- Spoiler:
trop joli le probleme supposons que a+b+c=1 ce qui est clairement vrai CQFD [spoiler/]
Dans la dérniére phase, Comment t'as su que a+b+c=1>=3b ?
- Citation :
- Problème 11: a,b,c sont des réels strictement positifs tels que :
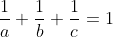
Montrer que :
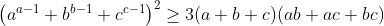
- Spoiler:
(a,b,c) > 0 Et 1/a + 1/b + 1/c = 1 Donc (a,b,c)>1 Et ab+bc+ac = abc
On sait que: (a^{a-1}+b^{b-1}+c^{c-1})² >= 3(a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1})
Il suffit donc de montrer que a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1} >= abc(a+b+c)
Qui est façile en supposant a>=b>=c Et remarque que a+b+c < ab+bc+ac = abc
Sauf error
Veuillez donner plus de détails sur ce qui est en rouge. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 01:14 | |
| - oussama1305 a écrit:
- M.Marjani a écrit:
- imanos a écrit:
- Salut
SOlution du probleme 9 :
- Spoiler:
trop joli le probleme supposons que a+b+c=1 ce qui est clairement vrai CQFD [spoiler/]
Dans la dérniére phase, Comment t'as su que a+b+c=1>=3b ?
- Citation :
- Problème 11: a,b,c sont des réels strictement positifs tels que :
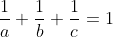
Montrer que :
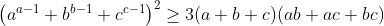
- Spoiler:
(a,b,c) > 0 Et 1/a + 1/b + 1/c = 1 Donc (a,b,c)>1 Et ab+bc+ac = abc
On sait que: (a^{a-1}+b^{b-1}+c^{c-1})² >= 3(a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1})
Il suffit donc de montrer que a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1} >= abc(a+b+c)
Qui est façile en supposant a>=b>=c Et remarquer que a+b+c < ab+bc+ac = abc
Sauf error
Veuillez donner plus de détails sur ce qui est en rouge. Bonsoir cher Oussama, desolé pour le retard. C'est façile de déduire que a+b+c < ab+bc+ac Car (a,b,c) > 1 Pour l'autre, "façile" car a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1} - abc(a+b+c) est équivalente au formule qui est plus simple: qui est clairement positive. Je n'attend que vos confirmations pour poster un EX. ( Et une explication du coté de Imanos :=) Bonne nuit ! | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 01:32 | |
| Bon, c'est confirmé, le truc avec la démonstration d'imanos c'est qu'on a : c <= 1/3.
Tu peux poster un autre exercice. | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 01:46 | |
| - oussama1305 a écrit:
- Bon, c'est confirmé, le truc avec la démonstration d'imanos c'est qu'on a : c <= 1/3.
Tu peux poster un autre exercice. Pardon, c'est juste. J'ai pas vu son supposition.   Hard luck ! | |
|
| | |
majdouline
Expert sup
Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 12:03 | |
| solution du problème 12:- Spoiler:
par l'inégalité de C.S.on a : 
sinon voulez vous vraiment continuer?parce que je crois que le problème de sylphaen est encore sans solution! | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 15:04 | |
| - majdouline a écrit:
- solution du problème 12:
- Spoiler:
par l'inégalité de C.S.on a :
sinon voulez vous vraiment continuer?parce que je crois que le problème de sylphaen est encore sans solution! Bonjour Melle Majdouline, juste précisez ou est l'error pour voir? Sinon vous bloquez le jeu sans résultat. - Spoiler:
(a,b,c) > 0 Et 1/a + 1/b + 1/c = 1 Donc (a,b,c)>1 Et abc = ab+bc+ac >= a+b+c On sait que: (a^{a-1}+b^{b-1}+c^{c-1})² >= 3(a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1}) Il suffit donc de montrer que a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1} - abc(a+b+c) >= 0 <=> Chose qui est vrai, En supposant a>=b>=c, donc a^a.b^b+a^a.c^c+b^b.c^c >= b^{a+b} + c^(a+c) + c^{b+c} >= (abc)^3 >= (abc)²(a+b+c) Sauf error !
Dernière édition par M.Marjani le Sam 21 Aoû 2010, 23:13, édité 2 fois | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 17:14 | |
| - majdouline a écrit:
- solution du problème 12:
- Spoiler:
par l'inégalité de C.S.on a :
sinon voulez vous vraiment continuer?parce que je crois que le problème de sylphaen est encore sans solution! Trois propositions : 1- Soit poster une solution alternative au problème. 2- Soit poster une inégalité. 3- Soit laisser Sylphaen poster une autre inégalité. | |
|
| | |
kira
Maître
Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 18:09 | |
| | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 18:12 | |
| | |
|
| | |
kira
Maître
Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 18:14 | |
| je m'excuse je n'ai rien pour l'instant a toi l'honneur  | |
|
| | |
Sylphaen
Expert sup
Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 18:24 | |
| Problème 13 : x,y,z sont des réels strictement positif t.q :  Montrer que :  | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 18:59 | |
|
Dernière édition par M.Marjani le Sam 21 Aoû 2010, 23:12, édité 1 fois | |
|
| | |
kira
Maître
Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 20:18 | |
| - M.Marjani a écrit:
-
- Citation :
- Problème 11: a,b,c sont des réels strictement positifs tels que :
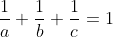
Montrer que :
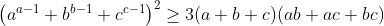
Solution 10:
- Spoiler:
( a,b,c) > 0 Et 1/a + 1/b + 1/c = 1 Donc (a,b,c)>1 Et abc = ab+bc+ac >= a+b+cOn sait que: (a^{a-1}+b^{b-1}+c^{c-1})² >= 3(a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1})
Il suffit donc de montrer que a^{a-1}*b^{b-1}+a^{a-1}*c^{c-1}+b^{b-1}*c^{c-1} - abc(a+b+c) >= 0
<=> Chose qui est vrai, En supposant a>=b>=c, donc a^a.b^b+a^a.c^c+b^b.c^c >= a^{ab} + c^(ac) + c^{bc} >= (abc)^3 >= (abc)²(a+b+c)Sauf error
En supposant a>=b>=c, donc a^a.b^b+a^a.c^c+b^b.c^c >= a^{ab} + c^(ac) + c^{bc} si on prend a=6 et b=3 et c=2 veuiilez calcurer i l'inego est satisfaite sauf erreur merci je supprimrai mon post après si il n'ya po de prob | |
|
| | |
M.Marjani
Expert sup
Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 23:32 | |
| - kira a écrit:
- Je supprimrai mon post après si il n'ya po de prob
- Spoiler:
Il reste toujours le probléme méme si tu supprime ton poste Kira : ) . Car a^a.b^b+a^a.c^c+b^b.c^c >= b^{a+b} + c^(a+c) + c^{b+c} >= (abc)^3 >= (abc)²(a+b+c)
C'est mieux de réflichir au probléme courant. | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 23:48 | |
| - Sylphaen a écrit:
- Problème 13 :
x,y,z sont des réels strictement positif t.q :
Montrer que :
Solution au probleme 13: - Spoiler:
on donne p=x+y+z ;xy+xz+yz=q ;xyz=r on a la fonction  est une fonction convexe sur [0+00[ donc l'inégalité équivaut à :  appliquant JEesen il s'ensuit qu'il suffit de démontrer que  apres on applique le fait de  </FONT> et  donc il suffit de démontrer que : ce qui est vrai par CS
Dernière édition par kholoud-tetouanie le Dim 22 Aoû 2010, 01:30, édité 5 fois (Raison : écrire en latex) | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Sam 21 Aoû 2010, 23:53 | |
| - kholoud-tetouanie a écrit:
- Sylphaen a écrit:
- Problème 13 :
x,y,z sont des réels strictement positif t.q :
Montrer que :
Solution au probleme 13:
- Spoiler:
on donne p=x+y+z ;xy+xz+yz=q ;xyz=r on a la fonction  est une fonction convexe sur [0+00[ donc l'inégalité équivaut à :  appliquant JEesen il s'ensuit qu'il suffit de démontrer que  apres on applique le fait de  et p²>=3p donc il suffit de démontrer que : ce qui est vrai par CSPS: au cas ou ça marche pas les images veuillez recopier ceci dans une réponse de mathlinks on a la fonction $\frac{1}{\sqrt{x}}donc
l'inégalité équivaut à :
$\sum \frac{x}{\sqrt{2y+2z}}+\sum \frac{yz}{\sqrt {2(x^2(y+z))}}\geq1$
appliquant JEesen il s'ensuit qu'il suffit de démontrer que
$\frac{p\sqrt{p}}{\sqrt{4q}}+\frac{q}{\sqrt{4r}}\geq1$
apres on applique le fait de $q^2\geq3pr$ et $p^2\geq3q$
donc il va ns suffir de démontrer que$ \sqrt{3p}\geq1$
ce qui est clairement vrai par CS
La réponse n'est pas lisible, veuillez utiliser du code LaTeX, parce que c'est très gênant. De plus, il y'a une erreur, le fait est que p^2>= 3p que tu as utilisé est fausse, contre-exemple : x=y=z=1/9 | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Dim 22 Aoû 2010, 00:03 | |
| Salut je suis désolé pour le Latex
tu copier ce que j'ai dit ici
http://www.artofproblemsolving.com/Forum/posting.php?mode=reply&f=151&&t=363149 et apres tu fait Preview la réponse est bien lisible
je voulais dir p²>=3q (juste faute dde frappe) | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Dim 22 Aoû 2010, 00:13 | |
| Ton utilisation de Jensen qui te permets de passer de:  À : J'avoue que j'aimerais plus d'explications, si c'est possible. Et merci d'avance. | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Dim 22 Aoû 2010, 00:17 | |
| Salut xf(2y+2z)+yf(2z+2x)+zf(2x+2y)>=(x+y+z)f(4(xy+xz+yz)/(x+y+z)) la meme chose pour l'autre ... je peux poster mon exercice mnt? | |
|
| | |
oussama1305
Expert grade1
Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
| | Sujet: Re: Le marathon des inégalités: Dim 22 Aoû 2010, 00:24 | |
| - kholoud-tetouanie a écrit:
- Salut xf(2y+2z)+yf(2z+2x)+zf(2x+2y)>=(x+y+z)f(4(xy+xz+yz)/(x+y+z))
la meme chose pour l'autre ...
je peux poster mon exercice mnt? Bien sûr, à toi l'honneur. | |
|
| | |
kholoud-tetouanie
Habitué
Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
| | Sujet: Re: Le marathon des inégalités: Dim 22 Aoû 2010, 00:50 | |
| Salut Probleme 14: ici tous les nombres sont des réels avec  MQ :  | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Le marathon des inégalités: | |
| |
|
| | |
| | Le marathon des inégalités: | |
|
