| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 22 Aoû 2010, 01:13 Dim 22 Aoû 2010, 01:13 | |
| j'aimerais proposer ma solution du 13ème problème: - Spoiler:
il est facile de prouver que :   1)-par l'inégalité de Hölder on a :  2)-par l'inégalité de Hölder on a :  ainsi en sommant 1)- et 2)- on aura: 
| |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 22 Aoû 2010, 02:23 Dim 22 Aoû 2010, 02:23 | |
| solution du problème 14:- Spoiler:
posons :  la condition devient donc:  et on a :  Et en utilisant l'inégalité de C.S on a donc :  sauf erreur....
| |
|
  | |
kholoud-tetouanie
Habitué
 Nombre de messages : 23 Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 22 Aoû 2010, 02:39 Dim 22 Aoû 2010, 02:39 | |
| Niice  A toi l'honneur  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 | |
  | |
kholoud-tetouanie
Habitué
 Nombre de messages : 23 Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 22 Aoû 2010, 22:32 Dim 22 Aoû 2010, 22:32 | |
| Salut solution au problem 15 - Spoiler:
very nice porbleme  supposons que x+y+z=1 L'inégalité équivaut a :  ce qui équivaut a: x+yz+27xy²z²>=27xyz(y²+z²+x) <==> x+yz+81xy²z²>=27xyz(x²-x+1) posons a=xyz ==> yz=a/x L'inégalité équivaut a :  *</STRONG> notons  cette fonction s'annule dans (apeu pres ) 0,03si x=<0;03 l'inégalité est bien vrai si x>=0;03 **en calculant le (delta) dans * on le trouve négative pour x £ [0;02;1/3] il s'ensuit qu'il suffit détudier le cas de x>=1/3 (dapres **)or f'(a)=162a+g(x)=<6+g(x)=<0 (x>=1/3)il s'ensuit que f(a) est une fonction décroissante qui atteind son minimum lorsque (a) atteind son maximum ce qui met fin a l'exerciceenfin sauf erreur ouuuf! cette fonction s'annule dans (apeu pres ) 0,03si x=<0;03 l'inégalité est bien vrai si x>=0;03 **en calculant le (delta) dans * on le trouve négative pour x £ [0;02;1/3] il s'ensuit qu'il suffit détudier le cas de x>=1/3 (dapres **)or f'(a)=162a+g(x)=<6+g(x)=<0 (x>=1/3)il s'ensuit que f(a) est une fonction décroissante qui atteind son minimum lorsque (a) atteind son maximum ce qui met fin a l'exerciceenfin sauf erreur ouuuf!
| |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 22 Aoû 2010, 23:03 Dim 22 Aoû 2010, 23:03 | |
| La méthode est bonne, quoi qu'elle mériterait plus d'explications.
Tu peux poster ton exercice. | |
|
  | |
kholoud-tetouanie
Habitué
 Nombre de messages : 23 Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Dim 22 Aoû 2010, 23:28 Dim 22 Aoû 2010, 23:28 | |
| Salut
Probleme 16 :
x,y,z sont des réels positifs tels que x²+y²+z²=1
MQ :
(2-3xy)(2-3xz)(2-3yz)>=1 | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 01:58 Lun 23 Aoû 2010, 01:58 | |
| Solution au problème 16- Spoiler:
Dédiée à celui qui se reconnaîtra  On pose :  La contrainte devient :  Quelques résultats préliminaires :  L'inégalité en question devient :  Et puisque :  , il nous suffit de démontrer que :  Ou bien que :  Ce qui est vrai par : 
J'attend une confirmation, voire une contre-confirmation.
Dernière édition par oussama1305 le Lun 23 Aoû 2010, 02:13, édité 1 fois | |
|
  | |
kholoud-tetouanie
Habitué
 Nombre de messages : 23 Nombre de messages : 23
Age : 31
Localisation : tetouan
Date d'inscription : 15/08/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 02:11 Lun 23 Aoû 2010, 02:11 | |
| Niice A toi l'honneur  | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 02:33 Lun 23 Aoû 2010, 02:33 | |
| Problème 17Prouver le lemme suivant : Montrer que pour tout réels strictement positifs a,b,c,x,y et z:  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 13:35 Lun 23 Aoû 2010, 13:35 | |
| - oussama1305 a écrit:
- Problème 17
Prouver le lemme suivant :
Montrer que pour tout réels strictement positifs a,b,c,x,y et z:
 Solution au problème 17 :- Spoiler:
Notations :
- "LHS" désigne le membre de gauche de l'inégalité.
- Sigma(a/(b+c)) désigne la somme cyclique : a/(b+c) + b/(a+c) + c/(a+b)
- Sigma (y+z) désigne la somme cyclique (y+z) + (x+z) + (x+y) = 2(x+y+z)
Preuve :
Par symétrie des rôles, supposons que a>=b>=c et z>=y>=x. Il est non difficile alors d'observer que les deux triplets (a/(b+c), b/(a+c), c/(a+b)) et (y+z, x+z, x+y) sont rangés en ordre décroissant.
De fait, en utilisant l'inégalité de Chebyschev, on a : LHS >= (Sigma(a/(b+c))*Sigma(y+z))/3 = 2Sigma(a/(b+c)(x+y+z)/3
En utilisant l'inégalité de Nesbitt : (Sigma(a/(b+c)) >= 3/2.
Par suite, il suffit de montrer que (x+y+z)² >= 3(xy+xz+yz), qui est un résultat classique.
Et je n'ai pas d'inégalité à proposer. Que chacun se sente libre d'en proposer une à ma place. EDIT : ma solution est fausse
Dernière édition par Dijkschneier le Lun 23 Aoû 2010, 15:38, édité 2 fois | |
|
  | |
kira
Maître

 Nombre de messages : 152 Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 14:29 Lun 23 Aoû 2010, 14:29 | |
| Problème 18
je me permet d'en proposer une pour faire avancer le jeu  Montrer que pour tout réels strictement positifs a,b,c :  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 14:30 Lun 23 Aoû 2010, 14:30 | |
| Dijkschneier je crois que ta solution est fausse..... Solution au problème 17 :
- Spoiler:
en utilisant l'inégalité de C.S. on a :  il suffit donc de prouver que :  ce qui est clairement vrai...
| |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 | |
  | |
kira
Maître

 Nombre de messages : 152 Nombre de messages : 152
Age : 32
Localisation : casablanca
Date d'inscription : 15/05/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 14:55 Lun 23 Aoû 2010, 14:55 | |
| et pour Dijkschneier fallait juste supposer que c>=b>=a et x>=y>=z saauf erreur | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 15:13 Lun 23 Aoû 2010, 15:13 | |
| - majdouline a écrit:
- Dijkschneier je crois que ta solution est fausse.....
Ah bon ? Et pourquoi ?  - kira a écrit:
- et pour Dijkschneier fallait juste supposer que c>=b>=a et x>=y>=z saauf erreur
Ça revient au même, n'est-ce pas ? Que les triplets soient rangés en ordre croissant ou décroissant n'a aucune influence, puisque la contrainte imposée par l'inégalité de Chebyschev est simplement que les deux triplets soient rangés dans un ordre semblable. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 15:21 Lun 23 Aoû 2010, 15:21 | |
| Je crois que tu ne peux pas supposer qu'on a x≥y≥z parce que l'inégalité n'est pas symétrique en x,y,z sauf pour a=b=c . | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 15:27 Lun 23 Aoû 2010, 15:27 | |
| - Dijkschneier a écrit:
- majdouline a écrit:
- Dijkschneier je crois que ta solution est fausse.....
Ah bon ? Et pourquoi ? 
une raison : par exemple le cas a>=b>=c et x>=y>=z ne peut pas être traité de la même manière  .... | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 15:33 Lun 23 Aoû 2010, 15:33 | |
| - majdouline a écrit:
- Dijkschneier je crois que ta solution est fausse.....
Solution au problème 17 :
- Spoiler:
en utilisant l'inégalité de C.S. on a :  il suffit donc de prouver que :  ce qui est clairement vrai...
Je n'ai pas compris ton passage avec CS, si tu pouvais expliquer un peu plus. Et merci. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 15:37 Lun 23 Aoû 2010, 15:37 | |
| - Sylphaen a écrit:
- Je crois que tu ne peux pas supposer qu'on a x≥y≥z parce que l'inégalité n'est pas symétrique en x,y,z sauf pour a=b=c .
- majdouline a écrit:
une raison :
par exemple le cas a>=b>=c et x>=y>=z ne peut pas être traité de la même manière  .... .... Oups...  En effet. Merci pour votre vigilance. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 15:44 Lun 23 Aoû 2010, 15:44 | |
| - oussama1305 a écrit:
- majdouline a écrit:
- Dijkschneier je crois que ta solution est fausse.....
Solution au problème 17 :
- Spoiler:
en utilisant l'inégalité de C.S. on a :  il suffit donc de prouver que :  ce qui est clairement vrai...
Je n'ai pas compris ton passage avec CS, si tu pouvais expliquer un peu plus.
Et merci. oui bien sur ...  | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 16:03 Lun 23 Aoû 2010, 16:03 | |
| - majdouline a écrit:
- oussama1305 a écrit:
- majdouline a écrit:
- Dijkschneier je crois que ta solution est fausse.....
Solution au problème 17 :
- Spoiler:
en utilisant l'inégalité de C.S. on a :  il suffit donc de prouver que :  ce qui est clairement vrai...
Je n'ai pas compris ton passage avec CS, si tu pouvais expliquer un peu plus.
Et merci. oui bien sur ...
 Très bien, vous pouvez poster une nouvelle inégalité. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 | |
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 17:14 Lun 23 Aoû 2010, 17:14 | |
| Solution du problème 19 : - Spoiler:
Par Hölder on a : 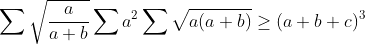 Et par AM-GM : 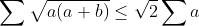 D'où : 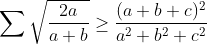 Donc il suffit de prouver que : 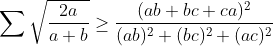 En posons a=1/x ,b=1/y,c=1/z ,x,y,z>0 il revient à prouver que : 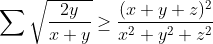 Ce qui est déjà fait .. sauf erreur ..
Problème 20 : Soit P un polynôme à coefficient réel : 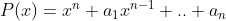 Et 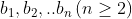 ses racines . Montrer que : 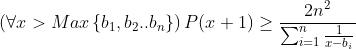
Dernière édition par Sylphaen le Lun 23 Aoû 2010, 17:45, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 23 Aoû 2010, 17:41 Lun 23 Aoû 2010, 17:41 | |
| Petite coquille : il s'agit de P(x+1) et non de f(x+1). | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
