<< Grand Jeu d'été 2011 de TC ->1ére >>

D'accord..
Je vais poster le prochain exercice

upsilon a écrit:

Solution du problème 28

Spoiler:

* IH=IH' ? - Vraiment, tu peux la démontrer ?

* vecteur{AI}.vecteur{AB'}=AI.AH
vecteur{AI}.vecteur{AC'}=AI.AH' - C'est plutôt vecteur{AI}.vecteur{AB'}=AH.AB' et vecteur{AI}.vecteur{AC'}=AC'.AH'

boubou math a écrit:

autre solution du problème 28

Spoiler:

C'est à toi le prochain problème.

upsilon a écrit:: D'accord..
Je vais poster le prochain exercice

Désolé, mais votre preuve était incomplète. C'est à boubou math de proposer un nouveau exercice puisqu'il a fait une preuve complète et bien rédigée.

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

Probleme 28
soient a,b,c,d >0 trouvez toutes les valeurs possible de la quantité :
<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Codeco13

Ma réponse pour problème 28:

Spoiler:

J'attends une confirmation...

En plus, je suis pas sûr de la partie SupE (Je crois qu'il existe un SupE).

Edit : Ma réponse est incomplète.

La quantité est clairement inférieure à 4.

Maître Nombre de messages : 189 Age : 30 Date d'inscription : 30/04/2011

boubou math a écrit:: Probleme 28
soient a,b,c,d >0 trouvez toutes les valeur possible de la quantité :

on a: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ alors: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ ou: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$

geom a écrit:

boubou math a écrit:: Probleme 28
soient a,b,c,d >0 trouvez toutes les valeur possible de la quantité :

on a: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ alors: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ ou: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$

$<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$

Vraiment, tu peux démontrer ?

a/(a+b+c+d)=<a/(a+b+d) =< a/(a+b)
b/(a+b+c+d)=<b/(a+b+c) =< b/(a+b)
c/(a+b+c+d)=<c/(d+b+c) =< c/(c+d)
d/(a+b+c+d)=<d/(a+d+c) =< d/(c+d)
Conclure.

Maître Nombre de messages : 189 Age : 30 Date d'inscription : 30/04/2011

on a: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ alors: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ de la meme maniere on prouve: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ et $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ et $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ . et on additionne les inégalités on trouve: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ donc: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

EXACTEMENT M.naoufal
on peut conclure que 1=<a/(a+b+c+d)+b/(a+b+c+d)+c/(a+b+c+d)+d/(a+b+c+d)=<2 donc toute les valeur possible de cette quantité sont dans l’intervalle [1,2]
ps: il faut trouver les cas d’égalité sinon c'est incomplet
a toi le nouveau exo

Maître Nombre de messages : 189 Age : 30 Date d'inscription : 30/04/2011

mais moi le premier qui poste le solution.

Pardon j'ai répondu à une question posée avant mon Post, j'ai pas vu que c'était un calcul d'un inf et un sup, sinon les cas d'égalité sont les valeurs Min et Max.
Je vous laisse proposer l'exo suivant.

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

a toi Geom Smile

Maître Nombre de messages : 189 Age : 30 Date d'inscription : 30/04/2011

probleme 29: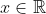
$<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ prouvez: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ et $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ .

on peut prouver que exp(ix)+exp(i(x+2*Pi/3))+exp(i(x+4*Pi/3))=0
la solution est :
puisque 1 +j + j^2=0 alors c'est bon.
j=exp(i*2Pi/3) = cos(2*Pi/3)+isin(2*Pi/3)
Pour l'exo proposé il s'en découle facilement en prenant les parties réelles et imaginaires.

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

n.naoufal a écrit:: on peut prouver que exp(ix)+exp(i(x+2*Pi/3))+exp(i(x+4*Pi/3))=0
la solution est :
puisque 1 +j + j^2=0 alors c'est bon.
j=exp(i*2Pi/3) = cos(2*Pi/3)+isin(2*Pi/3)
Pour l'exo proposé il s'en découle facilement en prenant les parties réelles et imaginaires.

c'est fait pour qu'un élève de tronc commun peut le résoudre

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

solution de problème 29

Spoiler:

boubou math a écrit:

solution de problème 29

Spoiler:

En gros c'est ça la méthode, mais il faut montrer que ce triangle ABC est équilatéral...

Et mentionner que les abscisses curvilignes de A, B et C sont x et x+2pi/3 et x+4pi/3

En tous cas, poste un nouveau exo.

Revenons à l'exo 28, les solutions proposées montrent que $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ . (avec E l'ensemble des valeurs de l'expression donnée)

Je crois qu'il faut préciser l'ensemble des valeurs de E (j'ai déjà montré une partie de l'exo (MinE=4/3) mais il reste la partie MaxE)

Et si MaxE=2, il faut chercher un cas d'égalité.

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

en effet les deux inégalité sont stricte car
a/(a+b+c+d)<a/(a+b+d) < a/(a+b)
b/(a+b+c+d)<b/(a+b+c) < b/(a+b)
c/(a+b+c+d)<c/(d+b+c) < c/(c+d)
d/(a+b+c+d)<d/(a+d+c) < d/(c+d)
parce que a,b,c,d différant de 0
et pour la solution que tu as posté je pense qu'on ne peut po supposer que a>=b>=c>=d car l’inégalité n'est pas symétrique .

boubou math a écrit:: en effet les deux inégalité sont stricte car
a/(a+b+c+d)<a/(a+b+d) < a/(a+b)
b/(a+b+c+d)<b/(a+b+c) < b/(a+b)
c/(a+b+c+d)<c/(d+b+c) < c/(c+d)
d/(a+b+c+d)<d/(a+d+c) < d/(c+d)
parce que a,b,c,d différant de 0
et pour la solution que tu as posté je pense qu'on ne peut po supposer que a>=b>=c>=d car l’inégalité n'est pas symétrique .

Tu peux poster une solution complète ?

Expert sup Nombre de messages : 521 Age : 29 Date d'inscription : 23/12/2010

geom a écrit:: on a: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ alors: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ de la meme maniere on prouve: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ et $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ et $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ . et on additionne les inégalités on trouve: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$ donc: $<< Grand Jeu d'été 2011 de TC ->1ére >> - Page 12 Gif$

voila mais toutes les inégalité sont stricte car
a+b<a+b+d<a+b+c+d donc a/a+b+c+d<a/a+b+d<a/a+b de même pour les autre thermes on additionne et on trouve l'inégalité souhaitée

» << L'Inscription au Grand Jeu d'été 2011 TC ->1ére >>
» c'est un grand grand grand défi
» grand defiiii !!!
» Lequel est le plus grand ?
» Le Grand Marathon d'eXo^^