| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
+20n.naoufal sadaso maths-au-feminin Hamouda geom Azerty1995 yasserito helloall Mehdi.A Mehdi.O Meded l'intellectuelle yasmine boubou math konica Nayssi az360 expert_run upsilon ali-mes 24 participants |
|
| Auteur | Message |
|---|
boubou math
Expert sup
 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 20:10 | |
| EXO 24
Dans le plan , on se donne 4 points tel que 3 quelconque forme un triangle,prouver qu'il existe au moins un triangle admettant 3 de ces point comme sommets,et dont l'un des angles n'est pas aigu.
| |
|
| | |
upsilon
Maître
 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 21:46 | |
| Solution de EXO 24 - Spoiler:
Puisque A et B et C forme un triangles et D est un point du meme plan Donc on peut conclure que ABCD forme un quadrilatére convexe ainsi angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}=360 On considère que angle{BAD}<90 angle{ABC}<90 angle{ADC}<90 angle{DCB}<90 Donc angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}<360 ce qui est impossible On peut donc conclure que l'un de ces angles n'est pas aigu Ainsi on peut avoir un triangles dont l'un des angles n'est pas aigu. [img]  [/img]
Qu'en pensez vous? | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 21:48 | |
| - upsilon a écrit:
- Solution de EXO 24
- Spoiler:
Puisque A et B et C forme un triangles et D est un point du meme plan Donc on peut conclure que ABCD forme un quadrilatére convexe
ainsi angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}=360 On considère que angle{BAD}<90 angle{ABC}<90 angle{ADC}<90 angle{DCB}<90 Donc angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}<360 ce qui est impossible On peut donc conclure que l'un de ces angles n'est pas aigu Ainsi on peut avoir un triangles dont l'un des angles n'est pas aigu. [img] [/img]
Qu'en pensez vous? ce qui est en rouge est faux on peut prendre un point au milieu du triangle | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:18 | |
| La réponse de upsilon est juste, si on prend un point dans le milieu de triangle, le quadrilatère sera concave est la relation des angles sera vérifiée. | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:24 | |
| - ali-mes a écrit:
- La réponse de upsilon est juste, si on prend un point dans le milieu de triangle, le quadrilatère sera concave est la relation des angles sera vérifiée.
ça solution reste incomplette | |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:28 | |
| - boubou math a écrit:
- upsilon a écrit:
- Solution de EXO 24
- Spoiler:
Puisque A et B et C forme un triangles et D est un point du meme plan Donc on peut conclure que ABCD forme un quadrilatére convexe
ainsi angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}=360 On considère que angle{BAD}<90 angle{ABC}<90 angle{ADC}<90 angle{DCB}<90 Donc angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}<360 ce qui est impossible On peut donc conclure que l'un de ces angles n'est pas aigu Ainsi on peut avoir un triangles dont l'un des angles n'est pas aigu. [img] [/img]
Qu'en pensez vous? ce qui est en rouge est faux on peut prendre un point au milieu du triangle
Si on prends un point au milieu du triangle dans ce cas là ce serait ABDC un quadrilatére convexe  dans tout les cas on dirait qu'il y a un angle qui n'est pas aigu en utilisant la meme methode. Ce qui est important que les point formeront un quadrilatére convexe et c'est tout, peu importe l'ordre des points ... Si les angles du quadrilatère convexe sont aigu Donc l'esemble de ces angles serait inférieur à 360 Ce qui impossible Donc il y a au moins un angle non aigu Ainsi on conclut qu'il ya au moins un triangle dont l'un des angles n'est pas aigu. | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:32 | |
| Bien  a toi de poster un problème . | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:40 | |
| - upsilon a écrit:
- boubou math a écrit:
- upsilon a écrit:
- Solution de EXO 24
- Spoiler:
Puisque A et B et C forme un triangles et D est un point du meme plan Donc on peut conclure que ABCD forme un quadrilatére convexe
ainsi angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}=360 On considère que angle{BAD}<90 angle{ABC}<90 angle{ADC}<90 angle{DCB}<90 Donc angle{BAD}+angle{ABC}+angle{ADC}+angle{DCB}<360 ce qui est impossible On peut donc conclure que l'un de ces angles n'est pas aigu Ainsi on peut avoir un triangles dont l'un des angles n'est pas aigu. [img] [/img]
Qu'en pensez vous? ce qui est en rouge est faux on peut prendre un point au milieu du triangle
Si on prends un point au milieu du triangle dans ce cas là ce serait ABDC un quadrilatére convexe
dans tout les cas on dirait qu'il y a un angle qui n'est pas aigu en utilisant la meme methode.
Ce qui est important que les point formeront un quadrilatére convexe et c'est tout, peu importe l'ordre des points ...
Si les angles du quadrilatère convexe sont aigu
Donc l'esemble de ces angles serait inférieur à 360
Ce qui impossible
Donc il y a au moins un angle non aigu
Ainsi on conclut qu'il ya au moins un triangle dont l'un des angles n'est pas aigu.
C'est plutôt concave. | |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:52 | |
| Voici le problème:
Exo 25
Indiquez le plus grand nombre N tel que N+40 et N-61 deux carrés de deux nombres entiers naturels
P.S :Je n'ai pas trouvé la solution mais si vous voulez que je change d'exercice il n'y a pas de problème | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 22:56 | |
| - upsilon a écrit:
- Voici le problème:
Exo 25
Indiquez le plus grand nombre N tel que N+40 et N-61 deux carrés de deux nombres entiers naturels
P.S :Je n'ai pas trouvé la solution mais si vous voulez que je change d'exercice il n'y a pas de problème N est entier naturel ou relatif ? | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:03 | |
| SOLUTION EXO 25
- Spoiler:
posons N+40=p² et N-61=q²---> N+40=q²+101
implique p²=q²+101
(p-q)(p+q)=101
101=1*101 (101 premier )
cela nous mène à ces deux systèmes suivants
1/
p-q=1
p+q=101
d'ou p=51 et q=50
2/
p-q=101
p+q=1
ce système n'a po de solution entière
donc le seul entier N qui satisfait ces condition la solution de l’équation
N+40=51² <---> n-61=50²
N=2561 cela finit la démonstration
| |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:15 | |
| | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:16 | |
| - boubou math a écrit:
- SOLUTION EXO 25
- Spoiler:
posons N+40=p² et N-61=q²---> N+40=q²+101
implique p²=q²+101
(p-q)(p+q)=101
101=1*101 (101 premier )
cela nous mène à ces deux systèmes suivants
1/
p-q=1
p+q=101
d'ou p=51 et q=50
2/
p-q=101
p+q=1
ce système n'a po de solution entière
donc le seul entier N qui satisfait ces condition la solution de l’équation
N+40=51² <---> n-61=50²
N=2561 cela finit la démonstration
D'où viens-tu avec ce cas ? Je crois que tu as raté quelques autres cas: (p et q sont de Z²) (p-q=-1 et p+q=-101) et (p-q=-101 et p+q=-1) Et puis tu résous ces quatre systèmes, dont les solutions doivent être entiers, et tu remplace dans N+40=p² et N-61=q² et tu prend la valeur maximale de N. Note: le couple (p,q) doit satisfaire N+40=p² et N-61=q² (il faut que tu aies la même valeur de N)
Mais en tous cas, c'est ça la méthode, donc boubou-math, à toi le prochain exo. | |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:20 | |
| - boubou math a écrit:
- SOLUTION EXO 25
- Spoiler:
posons N+40=p² et N-61=q²---> N+40=q²+101
implique p²=q²+101
(p-q)(p+q)=101
101=1*101 (101 premier )
cela nous mène à ces deux systèmes suivants
1/
p-q=1
p+q=101
d'ou p=51 et q=50
2/
p-q=101
p+q=1
ce système n'a po de solution entière
donc le seul entier N qui satisfait ces condition la solution de l’équation
N+40=51² <---> n-61=50²
N=2561 cela finit la démonstration
Bien , je n'ai pas pensé à cette méthode.. A toi donc le prochain exo.. | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:27 | |
| - ali-mes a écrit:
- boubou math a écrit:
- SOLUTION EXO 25
- Spoiler:
posons N+40=p² et N-61=q²---> N+40=q²+101
implique p²=q²+101
(p-q)(p+q)=101
101=1*101 (101 premier )
cela nous mène à ces deux systèmes suivants
1/
p-q=1
p+q=101
d'ou p=51 et q=50
2/
p-q=101
p+q=1
ce système n'a po de solution entière
donc le seul entier N qui satisfait ces condition la solution de l’équation
N+40=51² <---> n-61=50²
N=2561 cela finit la démonstration
D'où viens-tu avec ce cas ?
Je crois que tu as raté quelques autres cas: (p et q sont de Z²)
(p-q=-1 et p+q=-101) et (p-q=-101 et p+q=-1)
Et puis tu résous ces quatre systèmes, dont les solutions doivent être entiers, et tu remplace dans N+40=p² et N-61=q² et tu prend la valeur maximale de N.
Note: le couple (p,q) doit satisfaire N+40=p² et N-61=q² (il faut que tu aies la même valeur de N)
Mais en tous cas, c'est ça la méthode, donc boubou-math, à toi le prochain exo.
oué , mais la flemme d'écrire , je pense que le principe est simple , facile a comprendre .( le résultats reste correcte car la solution du système est +ou-50 / +ou-51 et comme on prend le carré , les cas que j'ai fait sont suffisant )
Dernière édition par boubou math le Ven 24 Juin 2011, 23:30, édité 1 fois | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:30 | |
| Suite à la demande de boubou-math, je poste un autre exercice (une équation fonctionnelle facile).
Problème 26:
Déterminer toutes les fonctions f définies sur R et vérifiant :
f(x²+y)=f(x)+f(y²)
| |
|
| | |
maths-au-feminin
Maître
Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:37 | |
| je réponds au problème 26
pour x=y=0 on a f(0)=2f(0) alors f(0)=0
pour y=0 on a f(x²)=f(x)+f(0) alors f(x²)=f(x)
pour y=-x² on a f(0)=f(x^4)+f(x) donc f(x^4)+f(x)=0 donc f(x²)+f(x)=0
alors f(x)=0 pour tt x de IR | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:44 | |
| - maths-au-feminin a écrit:
- je réponds au problème 26
pour x=y=0 on a f(0)=2f(0) alors f(0)=0
pour y=0 on a f(x²)=f(x)+f(0) alors f(x²)=f(x)
pour y=-x² on a f(0)=f(x^4)+f(x) donc f(x^4)+f(x)=0 donc f(x²)+f(x)=0
alors f(x)=0 pour tt x de IR Bien, mais juste une petite remarque, il faut toujours s'assurer que le fonction qu'on a dans la fin vérifie la condition de l'exercice, car lors de la résolution des équations fonctionnelles, on utilise des implications et pas des équivalences. En tous cas, à toi le prochain exo. | |
|
| | |
maths-au-feminin
Maître
Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 24 Juin 2011, 23:51 | |
| Problème 27:
soit ABCD un quadrilatère inscriptible et E un point de [BD] tel que BE=AB et F un point de [AC] tel que CD=CF. montrer que AED=AFD (angles) | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 25 Juin 2011, 00:25 | |
| Ma réponse pour problème 27:- Spoiler:
 On a:  et on a:  Et puisque le quadrilatère ABCD est cyclique donc  d'où  Et on a AB=BE donc ABE est isocèle en B d'où  Et on a:   Et on a: ) Et on a CD=CF donc CDF est isocèle en C d'où  Et on a:   Et on a: ) De (1) et (2) on conclut que:  (Remarquer qu'on peut conclure que AFED est aussi inscriptible)
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 25 Juin 2011, 00:33 | |
| Problème 28: (**) Soit ABC un triangle tel que  , et soit I le centre de son cercle inscrit. Et soit B' et C' les pieds des bissectrices des angles 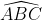 et 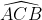 . Montrer que IB'=IC'. | |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 25 Juin 2011, 01:27 | |
| Solution du problème 28- Spoiler:
Soit H projection orthogonale de I sur [AC] et H' la projection orthogonale de I sur [AB]
I est le centre du cercle inscrit et H projection orthogonale de I sur [AC] et H' la projection orthogonale de I sur [AB]
Donc IH=IH'
Puisque H projection orthogonale de I sur [AC] et H' la projection orthogonale de I sur [AB]
Donc angle{IHA}=ANGLE{IH'A}=pi/2
Donc IHA et IH'A SONT DES TRIANGLES PERPENDICULAIRE
Selon la loi de pytagore on a AH²=AI²-IH et AH'²= AI²-IH'
Puisque IH=IH' on conclut que AH=AH'
Puisque [AI) est la bissectrice de angle{BAC} donc angle{IAB'}=angle{C'AI}=pi/6
en utilisant le produit scalaire on conclut que
vecteur{AI}.vecteur{AB'}=AI.AB'.cos(pi/6)=AI.AB'.(rac3)/2
vecteur{AI}.vecteur{AC'}=AI.AC'.cos(pi/6)=AI.AC'.(rac3)/2
ET d'une autre methode tant que H projection orthogonale de I sur [AC] et H' la projection orthogonale de I sur [AB]
ON A
vecteur{AI}.vecteur{AB'}=AI.AH
vecteur{AI}.vecteur{AC'}=AI.AH'
Donc
AI.AB'.(rac3)/2=AI.AC'.(rac3)/2
ainsi AB'=AC'
On considère les triangles IHB' et IHC'
On a H£[AB'] et H'£[AC']
donc B'H=B'A-HA ET H'C'=AC'-AH
Puisque AB'=AC' et AH=AH'
Donc B'H=H'C'
On a HB'=CH' et IH=IH' et angle{IHA}=ANGLE{IH'A}
Donc les deux triangles sont égaux
Ainsi on conclut que IB'=IC'
| |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 25 Juin 2011, 09:54 | |
| autre solution du problème 28 - Spoiler:
BIC=180-ICB-IBC
B'IC'=180-1/2(ABC+ACB)
B'IC'=180-1/2(180-60)
B'IC'=120
B'IC'+BAC=180 donc AB'IC' est un quadrilatère inscrit
or C'AI=IB'C' car il couvrent le même arc
et IAB'=IC'B' car il couvrent le même arc
d'ou IB'C'=IC'B'
donc IB'=IC'
Dernière édition par boubou math le Sam 25 Juin 2011, 13:24, édité 3 fois | |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 25 Juin 2011, 13:12 | |
| boubou math je n'ai compris dans ta solution, pourquoi B'IC'+ABC=180 ? | |
|
| | |
boubou math
Expert sup
Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sam 25 Juin 2011, 13:16 | |
| petite faute de frape c'est BAC je vais éditer | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> | |
| |
|
| | |
| | << Grand Jeu d'été 2011 de TC ->1ére >> | |
|
